Welcome!

Website Picture  

My name is Amin and I am an Acting Instructor in Applied Math at University of Washington. Below I briefly outline my research and teaching.
Curriculum Vitae [PDF]

It appears you don't have a PDF plugin for this browser. Please click here to download the PDF file.
Dissertation [PDF]

It appears you don't have a PDF plugin for this browser. Please click here to download the PDF file.

  • 4 Erdős
  • 7 Noether
  • 5 Blackwell
        Email: arahman2 [at] uw [dot] edu
        Office: Lewis Hall 116
        Office Phone: 206-685-8831
        Vehicle: Bicycle
        Twitter: @RTofTheMMAC
        YouTube: Amin Rahman @UW

My research involves formulating mechanistic dynamical models that agree with real world observations and analyzing them via dynamical systems theory, numerical methods, and data-driven techniques.  Brief summaries of recent projects can be found in the menus below, and I would be happy to share a more detailed research statement upon request.

  • Damped-driven systems

    Damped-driven systems are ubiquitous in nature from Physics to Sociology.  Heuristically, the concept of damped-driven systems is quite simple.  If we consider the un-damped un-forced ordinary differential equation (ODE)  x'' + ax = 0; a > 0, we know that the solutions can only be sinusoidal.  If we now add a damping term, bx', the solutions become more complex with exponential terms multiplying the sinusoidal terms.  Finally, if we drive the ODE with some non-autonomous forcing f(t), the system exhibits even more complex behavior and can even become chaotic if it no longer satisfies the hypothesis of the Poincaré–Bendixson theorem.

    Walking droplets:

    Walking DropletsHydrodynamic-Kinematic ModelIt has been known for decades that, given proper conditions, a fluid drop can be made to bounce on a vibrating fluid bath for long times scales.  In recent years, bouncing droplets have been observed to bifurcate from the bouncing state (no horizontal motion) to the walking state (horizontal motion).  Experiments with walking droplets (called walkers) exhibit analogs of wave-particle duality and more specifically quantum-like phenomena.  Studying walkers can enhance our understanding of quantum mechanics and suggest viable alternatives to the Copenhagen interpretation.

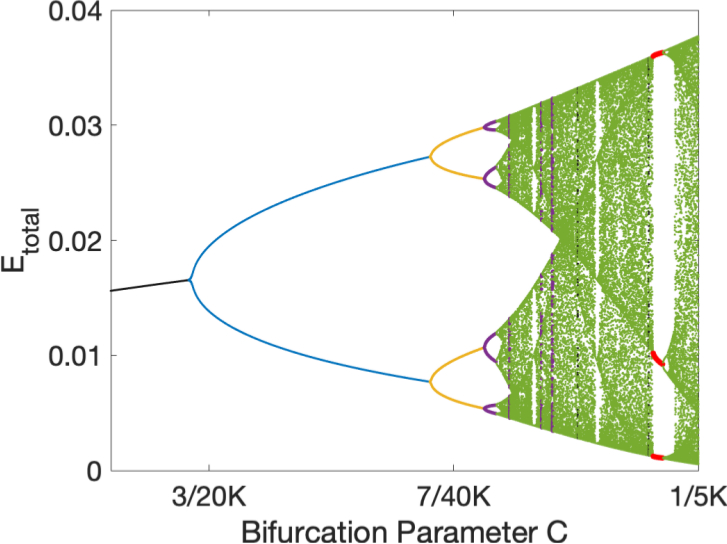    My research has focused on modeling walking droplet dynamics to analyze the long-time statistics and on Cobwebdeveloping experiments producing quantum-like behavior.  Recently, this has Period Doublingmanifested in modeling walkers on annulus and elliptical corrals with impurities, and analyzing those models via rigorous dynamical systems theory.  From the analysis we observe and prove that the droplets experience similar bifurcation behavior that is canonical to a wide class of damped-driven systems.  This theoretical will allow us to study the dynamical possibilities of such a system in parameter regimes that would not be possible on the macro-scale, thereby aiding us in asking questions about what happens at quantum-scales.  Further, in collaboration with Nathan Kutz and the AI Institute in Dynamic Systems, with equipment which Steve Brunton graciously allowed us to use, my students and I are conducting experiments on walking droplets to produce quantum-like behavior. We then use data-driven techniques such as statistical and machine learning to track the droplets and model the data in the form of differential equations.

    Animation of chaotic walking

    Animation of a single walker chaotically changing speed in an annulus.

    Animation of a chaotic walker

    Animation of a walker chaotically changing velocity.

    Relevant Publications:


    Logical circuits:

    RSFF experimentLogical circuits are an integral part of modern life that are traditionally designed with minimal uncertainty.  While this is straightforward to achieve with electronic logic, other logic families such as fluidic, chemical, and biological circuits naturally exhibit uncertainties due to the slower timescales of Boolean operations.  In addition, chaotic logical circuits have the potential to be employed in random number generation, encryption, and fault tolerance.  However, in order to exploit the properties of various nonlinear circuits they need to be studied further.  Since experiments with large systems become difficult, tractable mathematical models that are amenable to analysis via dynamical systems theory are of particular value.

    We developed a modeling framework for the chaotic Set/Reset flip-flop circuit and two types of chaotic NOR gates.  Through this framework we derive discrete dynamical models for Set/Reset - type circuits with any number of NOR gates.  Since the models are recurrence relations, the computational expense is quite low.  Further, we conducted experiments to test these models, which shows both qualitatively and quantitatively close behavior between the theory and experiments.
    RSFF plots


    Relevant Publications:




  • Physics-inspired modeling in the life sciences


    Similar phenomena often appear across many different branches of Science.  Cancer dynamics, infectious disease, and information cascades, often involve interactions of various agents.  Similar to Statistical Mechanics, these interactions appear random at the scale of a few agents, but average out at the scale of an entire population.

    Spatio-temporal cancer models:

    Drug DiffusionAccording to the National Cancer Institute, almost 40% of people in the United States end up developing cancer in their lifetime, and total national expenditure on cancer is $125 Billion.  While cancer deaths have fallen, the treatment of cancer is still predominant a trial and error process.  This may result in delays to administer the correct treatment, the use of more invasive procedures, or an increase in toxicity due to superfluous treatments.  Although these procedures may end up saving the patient, the treatment may also have an adverse effect on their quality of life.  To remedy this cruel paradox my collaborators and I have been developing a framework of complete scientific investigations for optimal treatment through the use of robust mathematical models and biological experiments rooted in the rigors of physics. Moreover, the President's recent moonshot has opened a singular opportunity for cancer modeling studies.

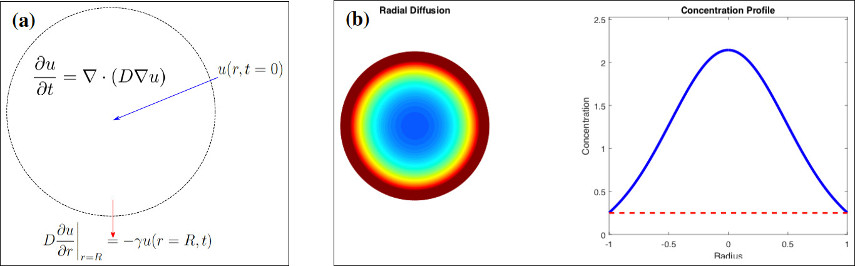
    Dynamical models for cancer often describe either transport (of cells, drugs, nutrients, etc.) or averaged population dynamics, but seldom both.  By coupling the two processes we are able to model a complete treatment strategy.  First, I developed a simplest case model for drug injection into a tumor coupled with tumor cell death.  Here (shown in the insert on the left) drug transport is modeled as radial diffusion with a leaky boundary obeying Newton's law of cooling, and the injection is modeled as an initial profile.  The population is modeled as a binary process where a cell that is exposed to higher amounts of a drug will have a greater chance of death, which on aggregate becomes deterministic:  the regions of the tumor with a higher than threshold conCAR T-cellcentration will ablate and the regions with lower concentration will remain.  This simplicity allows for fast computation, which is often necessary in real world scenarios.

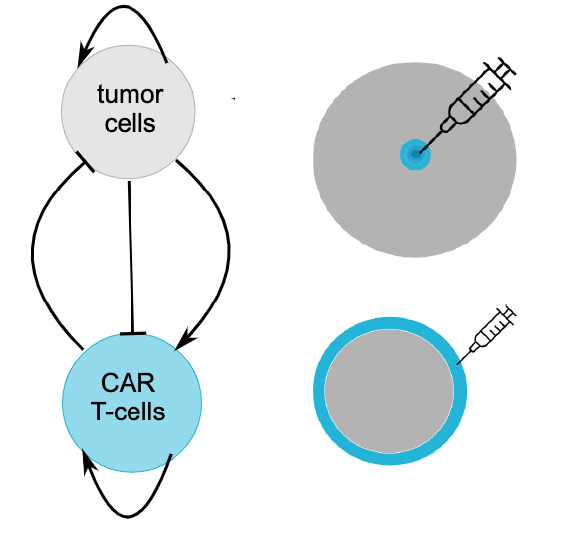
    More recently I have been collaborating with Katherine Owens and Ivana Bozic on the spatio-temporal dynamics of Chimeric antigen receptor T cell (CAR T-cell) therapies.  Treatments supplemented by CAR T-cells have shown clinical success in varieties of Leukemias and Lymphomas, and there have been promising studies on solid tumors as well.  Since the use of CAR T-cell therapies is still in its infancy, our work presents a singular opportunity for mathematical models to have an immense tangible impact on treatments that are currently being developed and those that will be developed in the near future.  For our seminal study, we model the interaction between CAR T-cells and a tumor as a coupled reaction-diffusion model as illustrated on the right.


    Spatio-temporal infectious disease models:

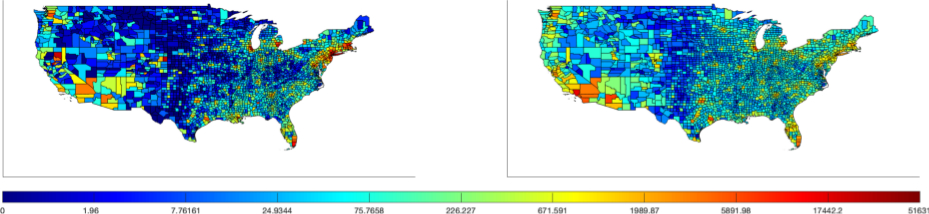    CovidI develop similar physics-inspired models for infectious disease.  The surprisingly mercurial Covid-19 pandemic highlights the need for spatio-temporal models in order to predict the next ``hot zone'' and properly allocate resources to those regions.  My collaborators, Angie Peace, Souparno Ghosh, Ramesh Kesawan, and I modeled highly asymptomatic disease transmission using county-wise data from the current pandemic, which importantly captures captures the evolution of hot zones, which was not previously possible with standard population dynamics.  Some preliminary results on the model simulation versus the actual data is shown on the left.


    Computational sociology:

    My MS student, Trevor, and I also developed a recurrence relation model for information cascades in social networks inspired by physical problems.  Using Twitter as an example, through this model we are able to forecast the virality of a tweet.  While most posts are innocuous, forecasting the virality of tweets that spread misinformation could help mitigate such a spread through targeted interventions.



    Animation of partial ablation

    Animation of partial ablation of a tumor.

    Animation of full ablation

    Animation of full ablation of a tumor.

    For more information please refer to my research statement.

    Relevant Publications:

    • Spatio-temporal models of infectious disease with high rates of asymptomatic transmission.
      A. Rahman, A. Peace, R. Kesawan, S. Ghosh.
      [Preliminary manuscript on Arxiv]
    • Tumor ablation due to inhomogeneous -- anisotropic diffusion in generic 3-dimensional topologies.
      E. Kara, A. Rahman, E. Aulisa, S. Ghosh.
      Physical Review E (2020). doi: 10.1103/PhysRevE.102.062425 [Preliminary manuscript on Arxiv]
    • Modeling of drug diffusion in a solid tumor leading to tumor cell death
      Aminur Rahman, Souparno Ghosh, and Ranadip Pal
      Physical Review E (2018). doi: 10.1103/PhysRevE.98.062408 [Preliminary manuscript on Arxiv]
    • Recursive model for dose-time responses in pharmacological studies
      Saugato R. Dhruba, Aminur Rahman, Raziur Rahman, Souparno Ghosh, and Ranadip Pal
      BMC Bioinformatics (2019). Invited special issue on Computational Network Biology: Modeling, Analysis, and Control. doi: 10.1186/s12859-019-2831-4
    • Recursive model for dose-time responses in pharmacological studies
      Aminur Rahman, S.R. Dhruba, Souparno Ghosh, and Ranadip Pal
      Proceedings of the Fifth International Workshop on Computational Network Biology: Modeling, Analysis, and Control (2018).
  • Theoretical Developments in Dynamical Systems and Bifurcations

    Theoretical developments in Dynamical Systems:

    Sigma map bifurcations:

    Upon discovering a new global bifurcation in discrete dynamical models of walking droplets, we developed a generic dynamical system in order to generalize the theory of such bifurcations.  From a graphical point of view, the invariant circle from an initial Neimark--Sacker bifurcation "blinks" on and off.  This is due to the transition from tangential to transverse intersections of the unstable and stable manifolds of the saddle fixed point.
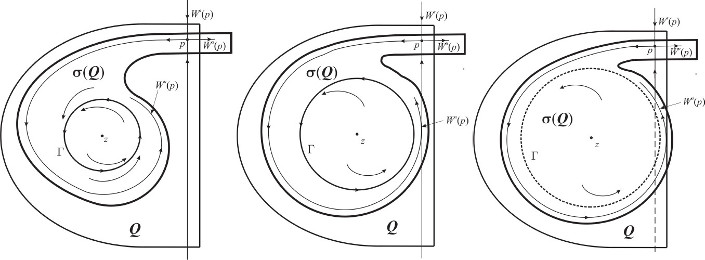
    Sigma map bifurcations

    Animation of colliding invariant circles

    Animation of colliding invariant circles during a global homoclinic-like bifurcation.

    Relevant Publications:

    • Sigma Map Dynamics and Bifurcations.
      Aminur Rahman, Yogesh Joshi, and Denis Blackmore
      Regular and Chaotic Dynamics (2017), Invited special issue dedicated to the memory of Vladimir Arnold (1937 - 2010). doi:10.1134/S1560354717060107
    • Interesting Bifurcations Inspired by Walking Droplet Dynamics
      Aminur Rahman and Denis Blackmore
      Communications in Nonlinear Science and Numerical Simulations (2020) doi: 10.1016/j.cnsns.2020.105348 [Preliminary manuscript on Arxiv]




    Generalized Attracting Horseshoe:

    We had previously shown that attracting horseshoes may be generalized to be contained within a quadrilateral trapping Trapping regionregion.  Through the NJIT Provost high school internship and the Provost Phase 1 undergraduate research grant, I mentored Karthik murthy (Bridgewater - Raritan High School) and Parth Sojitra (NJIT-ECE) in finding numerical evidence of generalized attracting horseshoes (GAH) in Poincare maps of the Rossler attractor.  I developed the algorithms to go from a first return map to a Poincare map and finally to find the quadrilateral trapping region for the supposed GAH.  I then guided our students in writing the MATLAB codes to carry out the algorithms.  While finding the trapping region numerically is not a proof, it does give us confidence that there exists a GAH in the Poincare map of the Rossler attractor.

    Relevant Publications:

    • Generalized Attracting Horseshoe in the Rossler Attractor.
      Karthik Murthy, Ian Jordan, Parth Sojitra, Aminur Rahman, and Denis Blackmore
      Symmetry (2021), Invited special issue on Symmetry in Modeling and Analysis of Dynamic Systems.doi: 10.3390/sym13010030 [Preliminary manuscript on Arxiv]
    • Generalized attracting horseshoes and chaotic strange attractors.
      Yogesh Joshi, Denis Blackmore, and Aminur Rahman




  • Miscellaneous

    Chaotic scattering:

    Chaotic scattering has been studied from the early 70s and 80s in solitary wave collisions from the Phi-Four equation (called Kink-Antikink collisions).  These were mainly numerical studies that gave insight into the phenomena.  However, since the equation is so difficult to work with there has been very little analysis done.  In more recent years reduction techniques have been used to approximate the Phi-Four PDE with a system of ODEs and also as an iterated map.

    We have gone further and developed a mechanical analog (a ball rolling on a special surface) of chaotic scattering in Kink-Antikink collisions.  This was done in order to conduct experiments.  In addition to experiments we have analyzed the system thoroughly, including the dissipation that comes from friction.  The experimental setup is shown bellow.

               


    Relevant Publications:

    • A mechanical analog of the two-bounce resonance of solitary waves: modeling and experiment.
      Roy H. Goodman, Aminur Rahman, Michael J. Bellanich, and Catherine N. Morrison.
      Chaos (2015), doi: 10.1063/1.4917047. [Arxiv]




    Pedagogical proof of Peixoto's theorem in 1-D:

    Peixoto's theorem is one of the most important theorems in Dynamical Systems.  It was proved by Dr. Mauricio Matos Peixoto in 1962.  This proof is extremely involved - far too involved for most undergraduate students to follow.  We develop an alternate - pedagogical proof of the simpler 1-D case, with the goal of allowing senior undergraduate students to follow and understand the proof and consequently some of the ideas involved in the much bigger proof of the 2-D case.

    Relevant Publications:

    • The One-dimensional Version of Peixoto's Structural Stability Theorem: A Calculus-based Proof.
      Aminur Rahman, Denis Blackmore.
      SIAM Review (2023)
    • Peixoto's structural stability theorem: the one dimensional version.
      Aminur Rahman.
      SIAM-dswebtutorials, (2013), eprint. Arxiv





    Particle Accelerator Physics:

    We numerically simulated the beam dynamics of the Energy Recovery Linear Particle Accelerator (ERL) design for Argonne National Lab's (ANL) Advanced Photon Source (APS).  The code BI, created by Ivan Bazarov, is benchmarked against our own code for simpler Accelerators.  Then the full ERL was simulated and the results were analyzed.  We concluded that the ERL, would be stable, and therefore a reasonable design for the specifications.

    Relevant Publications:

    • Benchmarking the multipass beam-breakup simulation code BI
      Aminur Rahman, Nicholas Sereno, and Hairong Shang
      OAG-TN-2008-029, (2008), [PDF]




Please click on the menus below for links, abstracts, and supplementary materials

Publications separated into Journals, Conference Proceedings, Dissertation, and Tutorials/Technical Notes.
Key: underline -- corresponding author, (g, ug, hs) -- students mentored (graduate, undergraduate, high school) at the time of publication, ► -- Highlighted publication


  • Universal dynamics of damped-driven systems: The logistic map as a normal form for energy balance. (under review)
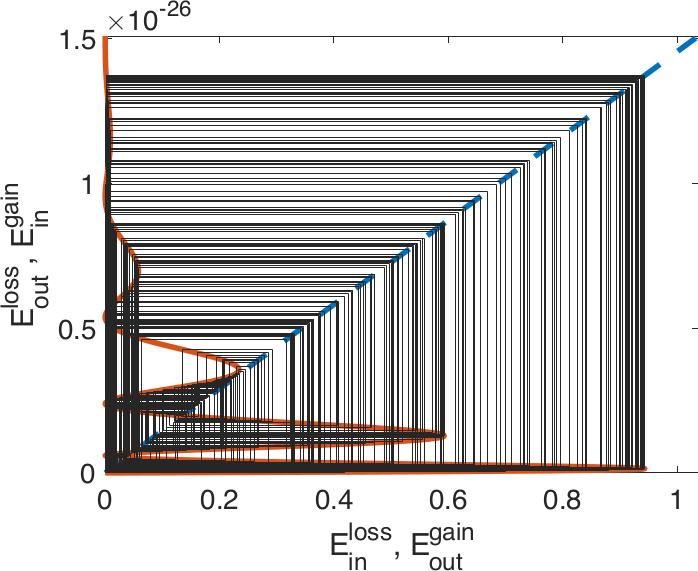
    Authors: J. Nathan Kutz, A. Rahman, M. Ebers, J. Koch, J. Bramburger.
    Sources: (under review) arxiv (preliminary manuscript)
    Abstract: Damped-driven systems are ubiquitous in engineering and science. Despite the diversity of physical processes observed in a broad range of applications, the underlying instabilities observed in practice have a universal characterization which is determined by the overall gain and loss curves of a given system. The universal behavior of damped-driven systems can be understood from a geometrical description of the energy balance with a minimal number of assumptions. The assumptions on the energy dynamics are as follows: the energy increases monotonically as a function of increasing gain, and the losses become increasingly larger with increasing energy, i.e. there are many routes for dissipation in the system for large input energy. The intersection of the gain and loss curves define an energy balanced solution. By constructing an iterative map between the loss and gain curves, the dynamics can be shown to be homeomorphic to the logistic map, which exhibits a period doubling cascade to chaos. Indeed, the loss and gain curves allow for a geometrical description of the dynamics through a simple Verhulst diagram (cobweb plot). Thus irrespective of the physics and its complexities, this simple geometrical description dictates the universal set of logistic map instabilities that arise in complex damped-driven systems. More broadly, damped-driven systems are a class of non-equilibrium pattern forming systems which have a canonical set of instabilities that are manifest in practice.
    Notes:
    Supplementary Materials
    Codes: Coming soon
    Animations:
  • Stochastic discrete dynamical model for the hydrodynamic analog of a quantum mirage. (under review)
    Authors: G. Ferrandez Quintoug, A. Rahman.
    Sources: (under review) arxiv (preliminary manuscript)
    Abstract: Recently discrete dynamical models of walking droplet dynamics have allowed for fast numerical simulations of their horizontal chaotic motion and consequently the long-time statistical distribution of the droplet position. We develop a discrete model for walkers on an elliptical corral with two dominant eigenmodes. These eigenmodes are excited periodically with each having random, but correlated, weights. At each iteration the model computes the horizontal propulsion of the droplet due to impacts with the fluid bath. The propulsion is calculated based on the interaction of the droplet with the wavefield produced by the eigenmode excitations. We record the long-time statistics, and incredibly for such a simple model, they are qualitatively similar to that of experiments.
    Notes:
    Supplementary Materials
    Codes: Coming soon
    Animations:
  • Multi-bounce resonances in the interaction of walking droplets. (under review)
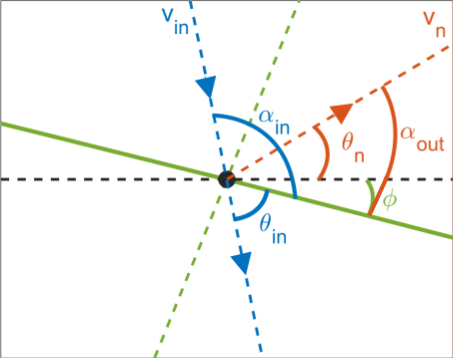
    Authors: G. Zhangug, I. C. Christov, A. Rahman.
    Sources: (under review) arxiv (preliminary manuscript)
    Abstract: Discrete dynamical models of walking droplets (walkers) have allowed swift numerical experiments revealing heretofore unobserved quantum statistics and related behaviors in a classical hydrodynamic system. One such model shows evidence of the empirically elusive n-bounce resonance and chaotic scattering in solitary-wave interactions investigated using covariant nonlinear field theory with polynomial self-interaction. We present experimentally testable predictions of n-bounce resonances between walkers. An exhaustive numerical investigation of the model reveals the usual fractal structure of resonances in the velocity in--velocity out diagram for colliding walkers. We suggest some avenues for further theoretical analysis of walker collisions, which may connect this discrete model back to the field-theoretic setting.
    Notes:
    Supplementary Materials
    Codes: Coming soon
    Animations:
  • Spatio-temporal models of infectious disease with high rates of asymptomatic transmission. (under review)
    Authors: A. Rahman, A. Peace., R. Kesawan.g, S. Ghosh..
    Sources: (under review) arxiv (preliminary manuscript)
    Abstract: The surprisingly mercurial Covid-19 pandemic has highlighted the need to not only accelerate research on infectious disease, but to also study them using novel techniques and perspectives. A major contributor to the difficulty of containing the current pandemic is due to the highly asymptomatic nature of the disease. In this investigation, we develop a modeling framework to study the spatio-temporal evolution of diseases with high rates of asymptomatic transmission, and we apply this framework to a hypothetical country with mathematically tractable geography; namely, square counties uniformly organized into a rectangle. We first derive a model for the temporal dynamics of susceptible, infected, and recovered populations, which is applied at the county level. Next we use likelihood-based parameter estimation to derive temporally varying disease transmission parameters on the state-wide level. While these two methods give us some spatial structure and show the effects of behavioral and policy changes, they miss the evolution of hot zones that have caused significant difficulties in resource allocation during the current pandemic. It is evident that the distribution of cases will not be stagnantly based on the population density, as with many other diseases, but will continuously evolve. We model this as a diffusive process where the diffusivity is spatially varying based on the population distribution, and temporally varying based on the current number of simulated asymptomatic cases. With this final addition coupled to the SIR model with temporally varying transmission parameters, we capture the evolution of "hot zones" in our hypothetical setup.
    Notes:
    Supplementary Materials
    Codes: Coming soon
    Animations:
  • ► Damped-driven system of bouncing droplets leading to deterministic diffusive behavior. Physical Review E 108 035103 (2023); DOI: 10.1103/PhysRevE.108.035103
    Authors: A. Rahman
    Sources: Physical Review arxiv (preliminary manuscript)
    Abstract: In recent decades computer-aided technologies have become prevalent in medicine, however, cancer drugs are often only tested on in vitro cell lines from biopsies. We derive a full three-dimensional model of inhomogeneous-anisotropic diffusion in a tumor region coupled to a binary population model, which simulates in vivo scenarios faster than traditional cell-line tests. The diffusion tensors are acquired using diffusion tensor magnetic resonance imaging from a patient diagnosed with glioblastoma multiform. Then we numerically simulate the full model with finite element methods and produce drug concentration heat maps, apoptosis hotpots, and dose-response curves. Finally, predictions are made about optimal injection locations and volumes, which are presented in a form that can be employed by doctors and oncologists.
    Notes:
    Supplementary Materials
    Codes: Codes [zip]
    Animations: N/A
  • ► Deep learning based object tracking in walking droplet and granular intruder experiments. Journal of Real-Time Image Processing 20 86 (2023); DOI: 10.1007/s11554-023-01341-4
    Authors: E. Kara, G. Zhangug, J. J. Williamsg, G. Ferrandez-Quintoug, L. J. Rhodenug, M. Kimug, J. Nathan Kutz, A. Rahman.
    Sources: Springer arxiv (preliminary manuscript)
    Abstract: We present a deep-learning based tracking objects of interest in walking droplet and granular intruder experiments. In a typical walking droplet experiment, a liquid droplet, known as walker, propels itself laterally on the free surface of a vibrating bath of the same liquid. This lateral motion stems from the interaction between the droplet and the wave it generates upon successive bounces off the vibrating liquid surface. A walker can exhibit a highly irregular trajectory over the course of its motion, including rapid acceleration and complex interactions with the other walkers present in the bath. In analogy with the hydrodynamic experiments, the granular matter experiments consist of a vibrating bath of very small solid particles and a larger solid called intruder. Like the fluid droplets, the intruder interacts with and travels the domain due to the waves of the bath but tends to move much slower and much less smoothly than the droplets. When multiple intruders are introduced, they also exhibit complex interactions with each other. We leverage the state-of-the-art object detection model YOLO (You Only Look Once) and the Hungarian Algorithm to accurately extract the trajectory of a walker or intruder in real-time. Our proposed methodology is capable of tracking individual walker(s) or intruder(s) in digital images acquired from a broad spectrum of experimental settings and does not suffer from any identity-switch issues. Thus, the deep learning approach developed in this work could be used to automatize the efficient, fast and accurate extraction of observables of interests in walking droplet, granular intruder experiments and similar particle tracking experiments. Such extraction capabilities are critically enabling for downstream tasks such as building data-driven dynamical models for the coarse-grained dynamics and interactions of the objects of interest.
    Notes: To feature in SIAM News
    Supplementary Materials
    Codes: Available with co-author E. Kara, github
    Animations: N/A
  • Walking droplets as a damped-driven system. SIAM J. Appl. Dyn. Syst. 22(2) (2023); DOI: 10.1137/22M1486042
    Authors: A. Rahman, J. Nathan Kutz.
    Sources: SIAM J. Appl. Dyn. Syst. arxiv (preliminary manuscript)
    Abstract: We consider the dynamics of a droplet on a vibrating fluid bath. This hydrodynamic quantum analog system is shown to elicit the canonical behavior of damped-driven systems, including a period doubling route to chaos. By approximating the system as a compositional map between the gain and loss dynamics, the underlying nonlinear dynamics can be shown to be driven by energy balances in the systems. The gain-loss iterative mapping is similar to a normal form encoding for the pattern forming instabilities generated in such spatially-extended system. Similar to mode-locked lasers and rotating detonation engines, the underlying bifurcations persist for general forms of the loss and gain, both of which admit explicit representations in our approximation. Moreover, the resulting geometrical description of the particle-wave interaction completely characterizes the instabilities observed in experiments.
    Notes:
    Supplementary Materials
    Codes: Codes [zip]
    Animations:
  • ► The One-dimensional Version of Peixoto's Structural Stability Theorem: A Calculus-based Proof. SIAM Review 65(3) (2023); DOI: 10.1137/21M1426572
    Authors: A. Rahman, D. Blackmore.
    Sources: SIAM Review arxiv (preliminary manuscript)
    Summary: Peixoto's structural stability and density theorems represent milestones in the modern theory of dynamical systems and their applications. Despite the importance of these theorems, they are often treated rather superficially, if at all, in upper level undergraduate courses on dynamical systems or differential equations. This is mainly because of the depth and length of the proofs. In this module, we formulate and prove the one-dimensional analogs of Peixoto's theorems in an intuitive and fairly simple way using only concepts and results that for the most part should be familiar to upper level undergraduate students in the mathematical sciences or related fields. The intention is to provide students who may be interested in further study in dynamical systems with an accessible one-dimensional treatment of structural stability theory that should help make Peixoto's theorems and their more recent generalizations easier to appreciate and understand. Further, we believe it is important and interesting for students to know the historical context of these discoveries since the mathematics was not done in isolation. The historical context is perhaps even more appropriate as it is the 100th anniversary of Marília Chaves Peixoto and Mauricio Matos Peixoto's births, February 24th and April 15th 1921, respectively.
    Notes: Cover article
    Supplementary Materials
    Codes: N/A Analysis
    Animations: N/A Analysis
  • Generalized Attracting Horseshoe in the Rossler Attractor. Symmetry 13 (1), 30 (2021); DOI: 10.3390/sym13010030
    Authors: K. Murthyhs, I. Jordanug, P. Sojitraug, A. Rahman, D. Blackmore.
    Sources: Symmetry arxiv (preliminary manuscript)
    Abstract: We show that there is a mildly nonlinear three-dimensional system of ordinary differential equations—realizable by a rather simple electronic circuit—capable of producing a generalized attracting horseshoe map. A system specifically designed to have a Poincaré section yielding the desired map is described, but not pursued due to its complexity, which makes the construction of a circuit realization exceedingly difficult. Instead, the generalized attracting horseshoe and its trapping region is obtained by using a carefully chosen Poincaré map of the Rössler attractor. Novel numerical techniques are employed to iterate the map of the trapping region to approximate the chaotic strange attractor contained in the generalized attracting horseshoe, and an electronic circuit is constructed to produce the map. Several potential applications of the idea of a generalized attracting horseshoe and a physical electronic circuit realization are proposed.
    Notes: Invited special issue on Symmetry in Modeling and Analysis of Dynamic Systems.
    Supplementary Materials
    Codes:
    Animations: N/A
  • ► Walking droplets through the lens of Dynamical Systems. Modern Physics Letters B 34 (34) 2030009 (2020); DOI: 10.1142/S0217984920300094.
    Authors: A. Rahman, D. Blackmore.
    Sources: World Scientific arxiv (preliminary manuscript)
    Abstract: Over the past decade the study of fluidic droplets bouncing and skipping (or "walking") on a vibrating fluid bath has gone from an interesting experiment to a vibrant research field. The field exhibits challenging fluids problems, potential connections with quantum mechanics, and complex nonlinear dynamics. We detail advancements in the field of walking droplets through the lens of Dynamical Systems Theory, and outline questions that can be answered using dynamical systems analysis. The article begins by discussing the history of the fluidic experiments and their resemblance to quantum experiments. With this physics backdrop, we paint a portrait of the complex nonlinear dynamics present in physical models of various walking droplet systems. Naturally, these investigations lead to even more questions, and some unsolved problems that are bound to benefit from rigorous Dynamical Systems Analysis are outlined.
    Notes: Invited World Scientific review article
    Supplementary Materials
    Codes: N/A Review article
    Animations: N/A Review article
  • ► Tumor ablation due to inhomogeneous -- anisotropic diffusion in generic 3-dimensional topologies. Physical Review E 102 062425 (2020); DOI: 10.1103/PhysRevE.102.062425
    Authors: E. Karag, A. Rahman, E. Aulisa, S. Ghosh.
    Sources: Physical Review arxiv (preliminary manuscript)
    Abstract: In recent decades computer-aided technologies have become prevalent in medicine, however, cancer drugs are often only tested on in vitro cell lines from biopsies. We derive a full three-dimensional model of inhomogeneous-anisotropic diffusion in a tumor region coupled to a binary population model, which simulates in vivo scenarios faster than traditional cell-line tests. The diffusion tensors are acquired using diffusion tensor magnetic resonance imaging from a patient diagnosed with glioblastoma multiform. Then we numerically simulate the full model with finite element methods and produce drug concentration heat maps, apoptosis hotpots, and dose-response curves. Finally, predictions are made about optimal injection locations and volumes, which are presented in a form that can be employed by doctors and oncologists.
    Notes:
    Supplementary Materials
    Codes: Available with co-author E. Kara
    Animations: N/A
  • Interesting bifurcations inspired by walking droplet dynamics. Communications in Nonlinear Science and Numerical Simulations 90 105348 (2020); DOI: 10.1016/j.cnsns.2020.105348
    Authors: A. Rahman, D. Blackmore.
    Sources: CNSNS arxiv (preliminary manuscript)
    Abstract: We identify two types of (compound) dynamical bifurcations generated primarily by interactions of an invariant attracting submanifold with stable and unstable manifolds of hyperbolic fixed points. These bifurcation types - inspired by recent investigations of mathematical models for walking droplet (pilot-wave) phenomena - are introduced and illustrated. Some of the one-parameter bifurcation types are analyzed in detail and extended from the plane to higher-dimensional spaces. A few applications to walking droplet dynamics are analyzed.
    Notes:
    Supplementary Materials
    Codes:
    Animations:
  • Recursive model for dose-time responses in pharmacological studies. BMC Bioinformatics 20 (Suppl 12): 317 (2019); DOI: 10.1186/s12859-019-2831-4.
    Authors: S.R. Dhrubag, A. Rahman, R. Rahmang, S. Ghosh., R. Pal.
    Sources: BMC
    Abstract: Clinical studies often track dose-response curves of subjects over time. One can easily model the dose-response curve at each time point with Hill equation, but such a model fails to capture the temporal evolution of the curves. On the other hand, one can use Gompertz equation to model the temporal behaviors at each dose without capturing the evolution of time curves across dosage.
    Notes: Invited special issue on Computational Network Biology: Modeling, Analysis, and Control.
    Supplementary Materials
    Codes: Available with co-author S.R. Dhruba
    Animations: N/A
  • ► Modeling of drug diffusion in a solid tumor leading to tumor cell death. Physical Review E 98 062408 (2018); DOI: 10.1103/PhysRevE.98.062408
    Authors: A. Rahman, S. Ghosh., R. Pal.
    Sources: Physical Review arxiv (preliminary manuscript)
    Abstract: It has been shown recently that changing the fluidic properties of a drug can improve its efficacy in ablating solid tumors. We develop a modeling framework for tumor ablation and present the simplest possible model for drug diffusion in a porous spherical tumor with leaky boundaries and assuming cell death eventually leads to ablation of that cell effectively making the two quantities numerically equivalent. The death of a cell after a given exposure time depends on both the concentration of the drug and the amount of oxygen available to the cell, which we assume is the same throughout the tumor for further simplicity. It can be assumed that a minimum concentration is required for a cell to die, effectively connecting diffusion with efficacy. The concentration threshold decreases as exposure time increases, which allows us to compute dose-response curves. Furthermore, these curves can be plotted at much finer time intervals compared to that of experiments, which may possibly be used to produce a dose-threshold-response surface giving an observer a complete picture of the drug's efficacy for an individual. In addition, since the diffusion, leak coefficients, and the availability of oxygen is different for different individuals and tumors, we produce artificial replication data through bootstrapping to simulate error. While the usual data-driven model with sigmoidal curves use 12 free parameters, our mechanistic model only has two free parameters, allowing it to be open to scrutiny rather than forcing agreement with data. Even so, the simplest model in our framework, derived here, shows close agreement with the bootstrapped curves and reproduces well-established relations, such as Haber's rule.
    Notes:
    Supplementary Materials
    Codes: Codes [zip]
    Animations: Animation of partial ablation

    Animation of partial ablation of a tumor.

    Animation of full ablation

    Animation of full ablation of a tumor.

  • ► Standard map-like models for single and multiple walkers in an annular cavity. Chaos 28 (9) 096102 (2018); DOI: 10.1063/1.5033949
    Authors: A. Rahman.
    Sources: Chaos arxiv (preliminary manuscript)
    Abstract: Recent experiments on walking droplets in an annular cavity showed the existence of complex dynamics including chaotically changing velocity. This article presents models, influenced by the kicked rotator/standard map, for both single and multiple droplets. The models are shown to achieve both qualitative and quantitative agreement with the experiments, and make predictions about heretofore unobserved behavior. Using dynamical systems techniques and bifurcation theory, the single droplet model is analyzed to prove dynamics suggested by the numerical simulations.
    Notes: Invited special issue on Hydrodynamic Quantum Analogs.
    Supplementary Materials
    Codes: Codes [zip]
    Animations: Animation of a walker with constant speed

    Animation of a single droplet walking around the annulus with constant speed.

    Animation of chaotic walking

    Animation of a single walker chaotically changing speed in an annulus.

    Animation of multiple walkers with constant speed

    Animation of multiple droplet walking around the annulus with constant speed.

    Animation of multiple walkers with destabilizing speed

    Animation of multiple droplet walking around the annulus with speeds starting to destabilize.

    Animation of multiple chaotic walkers

    Animation of multiple droplet walking around the annulus in a chaotic fashion.


  • Generalized attracting horseshoes and chaotic strange Attractors. (submitted)
    Authors: Y. Joshi, D. Blackmore, A. Rahman.
    Sources: arxiv (preliminary manuscript)
    Abstract: A generalized attracting horseshoe is introduced as a new paradigm for describing chaotic strange attractors (of arbitrary finite rank) for smooth and piecewise smooth maps f from Q to Q, where Q is a homeomorph of the unit interval in real m-space for any integer m > 1. The main theorems for generalized attracting horseshoes are shown to apply to Henon and Lozi maps, thereby leading to rather simple new chaotic strange attractor existence proofs that apply to a range of parameter values that includes those of earlier proofs.
    Notes:
    Supplementary Materials
    Codes: Available through co-author Y. Joshi
    Animations: N/A
  • ► Qualitative models and experimental investigation of chaotic NOR gates and set/reset flip-flops. Proceedings of the Royal Society A 474 1-19 (2018); DOI: 10.1098/rspa.2017.0111
    Authors: A. Rahman, I. Jordanug, D. Blackmore.
    Sources: Royal Society arxiv (preliminary manuscript)
    Abstract: It has been observed through experiments and SPICE simulations that logical circuits based upon Chua’s circuit exhibit complex dynamical behaviour. This behaviour can be used to design analogues of more complex logic families and some properties can be exploited for electronics applications. Some of these circuits have been modelled as systems of ordinary differential equations. However, as the number of components in newer circuits increases so does the complexity. This renders continuous dynamical systems models impractical and necessitates new modelling techniques. In recent years, some discrete dynamical models have been developed using various simplifying assumptions. To create a robust modelling framework for chaotic logical circuits, we developed both deterministic and stochastic discrete dynamical models, which exploit the natural recurrence behaviour, for two chaotic NOR gates and a chaotic set/reset flip-flop. This work presents a complete applied mathematical investigation of logical circuits. Experiments on our own designs of the above circuits are modelled and the models are rigorously analysed and simulated showing surprisingly close qualitative agreement with the experiments. Furthermore, the models are designed to accommodate dynamics of similarly designed circuits. This will allow researchers to develop ever more complex chaotic logical circuits with a simple modelling framework.
    Notes:
    Supplementary Materials
    Codes: Codes [zip]
    Animations: N/A
  • ► Sigma map dynamics and bifurcations. Regular and Chaotic Dynamics 22 (6) 740-749 (2017); DOI: 10.1134/S1560354717060107
    Authors: A. Rahman, Y. Joshi, D. Blackmore.
    Sources: Regular and Chaotic Dynamics
    Abstract: Some interesting variants of walking droplet based discrete dynamical bifurcations arising from diffeomorphisms are analyzed in detail. A notable feature of these new bifurcations is that, like Smale horseshoes, they can be represented by simple geometric paradigms, which markedly simplify their analysis. The two-dimensional diffeomorphisms that produce these bifurcations are called sigma maps or double sigma maps for reasons that are made manifest in this investigation. Several examples are presented along with their dynamical simulations.
    Notes: Invited special issue dedicated to the memory of Vladimir Arnold (1937 - 2010).
    Supplementary Materials
    Codes: Codes [zip]
    Animations: Animation of colliding invariant circles

    Animation of colliding invariant circles during a global homoclinic-like bifurcation.

  • Neimark--Sacker bifurcation and evidence of chaos in a discrete dynamical model of walkers. Chaos, Solitons & Fractals 91 339-349 (2016); DOI:10.1016/j.chaos.2016.06.016
    Authors: A. Rahman, D. Blackmore.
    Sources: CSF arxiv (preliminary manuscript)
    Abstract: Bouncing droplets on a vibrating fluid bath can exhibit wave-particle behavior, such as being propelled by interacting with its own wave field. These droplets seem to walk across the bath, and thus are dubbed walkers. Experiments have shown that walkers can exhibit exotic dynamical behavior indicative of chaos. While the integro-differential models developed for these systems agree well with the experiments, they are difficult to analyze mathematically. In recent years, simpler discrete dynamical models have been derived and studied numerically. The numerical simulations of these models show evidence of exotic dynamics such as period doubling bifurcations, Neimark–Sacker (N–S) bifurcations, and even chaos. For example, in [1], based on simulations Gilet conjectured the existence of a supercritical N-S bifurcation as the damping factor in his one- dimensional path model. We prove Gilet’s conjecture and more; in fact, both supercritical and subcritical (N-S) bifurcations are produced by separately varying the damping factor and wave-particle coupling for all eigenmode shapes. Then we compare our theoretical results with some previous and new numerical simulations, and find complete qualitative agreement. Furthermore, evidence of chaos is shown by numerically studying a global bifurcation.
    Notes:
    Supplementary Materials
    Codes: Codes [zip]
    Animations: Animation of a walker before N--S bifurcation

    Animation of a walker converging to a fixed position before the Neimark--Sacker bifurcations.

    Animation of a walker after the first N--S bifurcation

    Animation of a walker converging to a fixed path determined by an invariant circle.

    Animation of a walker after the second N--S bifurcation

    Animation of a walker converging to a fixed path determined by an invariant circle after bypassing a homoclinic orbit.

    Animation of a walker after the third N--S bifurcation

    Animation of a walker converging to a fixed path determined by an invariant circle.

    Animation of a walker after colliding invariant circles

    Animation of a walker trapped in an orbit created by intertwined invariant circle.

    Animation of a chaotic walker

    Animation of a walker chaotically changing velocity.

  • ► A mechanical analog of the two-bounce resonance of solitary waves: modeling and experiment. Chaos 25 043109 (2015); DOI:10.1063/1.4917047
    Authors: R. Goodman, A. Rahman, M.J. Bellanich, C.N. Morrison.
    Sources: Chaos arxiv (preliminary manuscript)
    Abstract: We describe a simple mechanical system, a ball rolling along a specially-designed landscape, which mimics the well-known two-bounce resonance in solitary wave collisions, a phenomenon that has been seen in countless numerical simulations but never in the laboratory. We provide a brief history of the solitary wave problem, stressing the fundamental role collective-coordinate models played in understanding this phenomenon. We derive the equations governing the motion of a point particle confined to such a surface and then design a surface on which to roll the ball, such that its motion will evolve under the same equations that approximately govern solitary wave collisions. We report on physical experiments, carried out in an undergraduate applied mathematics course, that seem to exhibit the two-bounce resonance.
    Notes:
    Supplementary Materials
    Codes: Codes available through R. Goodman
    Animations:
  • Discrete dynamical modeling and analysis of the R-S flip-flop circuit. Chaos, Solitons & Fractals 42 951-963 (2009); DOI:10.1016/j.chaos.2009.02.032
    Authors: D. Blackmore, A. Rahman, J. Shah.
    Sources: CSF arxiv (preliminary manuscript)
    Abstract: A simple discrete planar dynamical model for the ideal (logical) R–S flip-flop circuit is developed with an eye toward mimicking the dynamical behavior observed for actual physical realizations of this circuit. It is shown that the model exhibits most of the qualitative features ascribed to the R–S flip-flop circuit, such as an intrinsic instability associated with unit set and reset inputs, manifested in a chaotic sequence of output states that tend to oscillate among all possible output states, and the existence of periodic orbits of arbitrarily high period that depend on the various intrinsic system parameters. The investigation involves a combination of analytical methods from the modern theory of discrete dynamical systems, and numerical simulations that illustrate the dazzling array of dynamics that can be generated by the model. Validation of the discrete model is accomplished by comparison with certain Poincaré map like representations of the dynamics corresponding to three-dimensional differential equation models of electrical circuits that produce R–S flip-flop behavior.
    Notes:
    Supplementary Materials
    Codes:
    Animations:


  • Qualitative Modeling of Chaotic Logical Circuits and Walking Droplets: A Dynamical Systems Approach. (2017)
    Authors: A. Rahman
    Sources: NJIT Library
    Abstract:

    Logical circuits and wave-particle duality have been studied for most of the 20th century. During the current century scientists have been thinking differently about these well-studied systems. Specifically, there has been great interest in chaotic logical circuits and hydrodynamic quantum analogs.

    Traditional logical circuits are designed with minimal uncertainty. While this is straightforward to achieve with electronic logic, other logic families such as fluidic, chemical, and biological, naturally exhibit uncertainties due to their inherent nonlinearity. In recent years, engineers have been designing electronic logical systems via chaotic circuits. While traditional boolean circuits have easily determined outputs, which renders dynamical models unnecessary, chaotic logical circuits employ components that behave erratically for certain inputs.

    There has been an equally dramatic paradigm shift for studying wave-particle systems. In recent years, experiments with bouncing droplets (called walkers) on a vibrating fluid bath have shown that quantum analogs can be studied at the macro scale. These analogs help us ask questions about quantum mechanics that otherwise would have been inaccessible. They may eventually reveal some unforeseen properties of quantum mechanics that would close the gap between philosophical interpretations and scientific results.

    Both chaotic logical circuits and walking droplets have been modeled as differential equations. While many of these models are very good in reproducing the behavior observed in experiments, the equations are often too complex to analyze in detail and sometimes even too complex for tractable numerical solution. These problems can be simplified if the models are reduced to discrete dynamical systems. Fortunately, both systems are very naturally time-discrete. For the circuits, the states change very rapidly and therefore the information during the process of change is not of importance. And for the walkers, the position when a wave is produced is important, but the dynamics of the droplets in the air are not.

    This dissertation is an amalgam of results on chaotic logical circuits and walking droplets in the form of experimental investigations, mathematical modeling, and dynamical systems analysis. Furthermore, this thesis makes connections between the two topics and the various scientific disciplines involved in their studies.



Invited Talks:

  • Nonlinear Dynamics, Bifurcations, and Chaos: The Works of Denis Blackmore.
    Society for Industrial and Applied Mathematics Dynamical Systems 2023, Hilton, Portland, OR, May 15, 2023.
  • Walking droplets as a damped-driven system.
    Fluid Mechanics Seminar, New Jersey Institute of Technology, Newark, NJ, December 5, 2022.
  • Walking droplets as a damped-driven system.
    Physical Applied Math Seminar, Massachusetts Institute of Technology, Cambridge, MA, November 16, 2022.
  • Spatio-temporal models of cancer treatments.
    Dynamical Systems Seminar, Boston University, Boston, MA, November 15, 2022.
  • Simple Models in a Complex World: From Physics to Sociology.
    Albert Dorman Honors College Colloquium, New Jersey Institute of Technology, Newark, NJ, November 2, 2022.
  • Early Career Reserach Panel for Undergraduate Applied Math Majors.
    Department of Applied Mathematics, University of Washington, Seattle, WA, January 25, 2022.
  • Diffusive behavior in walking droplets.
    Society for Industrial and Applied Mathematics Dynamical Systems 2021.
    Note 1: Virtual Conference
  • [Video] Physics-based models of cancer drug response in solid tumors: towards computer-aided treatment strategies.
    Biomath Seminar, University of Nebraska, Lincoln, NE, February 18, 2021.
  • Diffusive behavior in walking droplets.
    American Physical Society March Meeting, Denver, CO, March 2, 2020.
    Note 1: GSNP Virtual session held on March 4th due to cancelation of APS March
    Note 2: GSNP Postdoctoral Speaker Award Finalist
  • Mathematically Tractable Models in a Complex World: From Physics to Biology.
    Math Seminar, University of Kentucky, Lexington, KY, January 24, 2020.
  • Simple proofs of chaos for logical circuit and walking droplet models.
    SIAM Dynamical Systems 2019, Snowbird Resort, Snowbird, UT, May 20, 2019
  • Coupled transport-population models for drug distribution and tumor cell death.
    Rennes Physics Seminar, Universite de Rennes, Rennes, FR, April 16, 2019
  • Mathematically tractable models in cancer biophysics and walking droplets.
    TTU SIAM Chapter Early Career Colloquium, Texas Tech University, Lubbock, TX, February 26, 2019
  • Coupled transport-population models for drug distribution and tumor cell death.
    Mechanical Engineering Seminar, Purdue University, West Lafayette, IN, January 9, 2019
  • Simple transport-population models for drug distribution and tumor cell death.
    Applied mathematics Seminar, Texas Tech University, Lubbock, TX, November 28, 2018
  • Simple transport-population models for drug distribution and tumor cell death.
    Biomathematics Seminar, Texas Tech University, Lubbock, TX, November 6, 2018
  • Discrete dynamical models of walking droplets.
    Applied mathematics Seminar, Texas Tech University, Lubbock, TX, October 31, 2018
  • Tumor ablation through drug diffusion.
    Mathematical Biology Seminar, New Jersey Institute of Technology, Newark, NJ, April 3, 2018
  • Simple Models in a Complex World.
    SIAM TTU Graduate Student Chapter Junior Scholar Symposium, Texas Tech University, Lubbock, TX, February 27, 2018
  • Tumor ablation through drug diffusion.
    Biomathematics Seminar, Texas Tech University, Lubbock, TX, February 6, 2018
  • Bifurcations in Walking Droplet Dynamics.
    SIAM Dynamical Systems Conference 2017, Snowbird Resort, Snowbird, UT, May 21, 2017
  • Dynamical modeling and analysis of walking droplets and chaotic logical circuits.
    Numerical Methods for PDEs Seminar, Massachusetts Institute of Technology, Cambridge, MA, February 22, 2017
  • Dynamical modeling and analysis of chaotic logical circuits and walking droplets.
    Dynamical Systems Seminar, University of Rhode Island, South Kingstown, RI, February 8, 2017
  • Neimark-Sacker Bifurcation and Evidence of Chaos in a Discrete Dynamical Model of Walkers.
    AMS Fall Northeast Sectional Conference 2015, Rutgers University, New Brunswick, NJ, November 14, 2015
  • The Chaotic Ballet of Walking Droplets.
    Mechanical and Industrial Engineering Colloquium, New Jersey Institute of Technology, Newark, NJ, October 7, 2015
  • A Scheme for Modeling and Analyzing the Dynamics of Logical Circuits
    Center for Nonlinear Studies Seminar, Los Alamos National Laboratory, Los Alamos, NM, May 21, 2015
  • A Scheme for Modeling and Analyzing the Dynamics of Logical Circuits
    SIAM Dynamical Systems Conference 2015, Snowbird Resort, Snowbird, UT, May 18, 2015
  • A Mechanical Analog and Discrete Modeling of the n-bounce Resonance of Solitary Waves.
    AMS Spring Northeast Sectional Conference 2015, Georgetown University, Washington DC, March 7, 2015
  • Further Analysis of Discrete Dynamical Models of the RS Flip-Flop Circuit
    AMS Fall Southeast Sectional Conference 2014, University of North Carolina at Greensboro, Greensboro, NC, November 8, 2014
  • [Video] A Scheme for Modeling and Analyzing the Dynamics of Logical Circuits
    AMS Spring Sectional Northeast Conference 2014, University of Maryland Baltimore County, Baltimore, MD, March 29, 2014

Contributed Talks:

  • Diffusive behavior in walking droplets.
    American Physical Society March Meeting, Denver, CO, March 6, 2020.
    Note 1: GSOFT Virtual session held on March 2nd due to cancelation of APS March
  • The Chaotic Ballet of Walking Droplets.
    Dynamic Days 2018, Hilton Denver City Center, Denver, CO, January 4, 2018
  • Dynamics of Discrete Dynamical Models of a Walker in an Annulus.
    Workshop on Wave-Particle Duality and Hydrodynamic Quantum Analogs, University of Liège, Liège, BE., July 3, 2017
  • The Chaotic Ballet of Walking Droplets.
    Joint Math Meetings, Hyatt Regency Atlanta and Marriott Atlanta Marquis, Atlanta, GA, January 4, 2017
  • Neimark-Sacker Bifurcation and Evidence of Chaos in a Discrete Dynamical Model of Walkers.
    American Mathematical Society Fall Northeast Sectional Conference 2016, Bowdoin College, Brunswick, ME, September 24, 2016
  • A Tempest in The Mathematics of Time: A brief history of chaos and its appearance in walking droplets and electronic circuits.
    NJIT Graduate Student Seminar, New Jersey Institute of Technology, Newark, NJ, June 21, 2016
  • Neimark-Sacker Bifurcation and Evidence of Chaos in a Discrete Dynamical Model of Walkers.
    APS 68th Annual Division of Fluid Dynamics Meeting, Hynes Convention Center, Boston, MA, November 24, 2015
  • Neimark-Sacker Bifurcation and Evidence of Chaos in a Discrete Dynamical Model of Walkers.
    NJIT Graduate Student Seminar, New Jersey Institute of Technology, Newark, NJ, June 11, 2015
  • A Mechanical Analog of the Chaotic Scattering in Solitary Waves.
    NJIT Graduate Student Seminar, New Jersey Institute of Technology, Newark, NJ, July 24, 2014
  • Peixoto's structural stability theorem:  the one-dimensional version.
    Joint Mathematics Meetings 2014, Baltimore, MD, January 17, 2014
  • A Scheme for Modeling and Analyzing the Dynamics of Logical Circuits
    Joint Mathematics Meetings 2014, Baltimore, MD, January 15, 2014
  • Phase Field Formulation for Microstructure Evolution in Oxide Ceramics.
    Modeling Problems in Industry 2013, Worcester Polytechnic Institute, Worcester, MA, June 21, 2013
  • Peixoto's Structural Stability Theorem:  The One-dimensional Version.
    NJIT Graduate Student Seminar, New Jersey Institute of Technology, Newark, NJ, June 11, 2013
  • Logical circuits: A Scheme for Discrete Modeling and Analysis.
    NJIT Graduate Student Seminar, New Jersey Institute of Technology, Newark, NJ, July 10, 2012
  • Mechanical Chaotic Scattering: The Adventures in the Valley of Chaos.
    Hallenbeck Graduate Student Seminar, University of Delaware, Newark, DE, April 20, 2011
  • A Scheme for Modeling and Analyzing the Dynamics of Logical Circuits.
    Hallenbeck Graduate Student Seminar, University of Delaware, Newark, DE, October 20, 2010

Posters:

  • Physics-based models and simulations of cancer drug response in solid tumors
    American Physical Society March Meeting, March 16, 2021
    Note 1: Virtual
    Note 2: First-prize in FECS poster award
  • Standard map-like models for single and multiple walkers in an annular cavity
    Dynamic Days 2019, Hilton Orrington Hotel, Evanston, IL, January 4 - 6, 2019
  • A prospective analysis tool to assess potential success for extra-femoral mechanical thrombectomy
    Congress of Neurological Surgeons 2018, Mariott Marquis, Houston, TX, October 6 - 11, 2018
  • A Scheme for Analyzing the Dynamics of Logical Circuits
    Frontiers in Applied and Computational Mathematics 2015, New Jersey Institute of Technology, Newark, NJ, June 5 - 6, 2015
  • A Scheme for Analyzing the Dynamics of Logical Circuits
    Frontiers in Applied and Computational Mathematics 2014, New Jersey Institute of Technology, Newark, NJ, May 22 - 23, 2014
  • A Scheme for Analyzing the Dynamics of Logical Circuits
    Joint Mathematics Meetings 2014, Baltimore, MD, January 16, 2014
  • A Scheme for Analyzing the Dynamics of Logical Circuits
    Graduate Student Association Research Day 2013, New Jersey Institute of Technology, Newark, NJ, October 31, 2013
  • A Scheme for Analyzing the Dynamics of Logical Circuits
    Frontiers in Applied and Computational Mathematics 2013, New Jersey Institute of Technology, Newark, NJ, May 31 - June 2, 2013
  • A Scheme for Analyzing the Dynamics of Logical Circuits
    Frontiers in Applied and Computational Mathematics 2010, New Jersey Institute of Technology, Newark, NJ, May 21 - 23, 2010
  • Discrete Dynamical Modeling and Analysis of the R-S flip-flop circuit
    NJIT Experience Day, New Jersey Institute of Technology, Newark, NJ, April 19, 2009
  • Discrete Dynamical Modeling and Analysis of the R-S flip-flop circuit
    Dana Knox Student Research Showcase, New Jersey Institute of Technology, Newark, NJ, April 8, 2009
  • Discrete Dynamical Modeling and Analysis of the R-S flip-flop circuit
    Garden State Undergraduate Mathematics Conference, Monmouth University, Monmouth, NJ, March 29, 2009
  • Chaos of the R-S flip-flop circuit
    Frontiers in Applied and Computational Mathematics 2008, New Jersey Institute of Technology, Newark, NJ, May 19 - 21, 2008
  • Chaos of the R-S flip-flop circuit
    NJIT Experience Day, New Jersey Institute of Technology, Newark, NJ, April 5, 2008

I have included lecture notes in the menus below.


Graduate courses:

Recitations:

  1. Calculus II (NJIT)
  2. Calculus I (NJIT)
  3. Calculus I (UD)
  4. Pre-Calculus (NJIT)

As guest lecturer:

  1. Complex Variables (NJIT)
  2. Real Analysis (NJIT)
  3. Dynamical Systems (NJIT)
  4. Linear Algebra (NJIT)
  5. Ordinary Differential Equations (NJIT)
  6. Numerical Methods Lab (NJIT)
  7. Calculus II (NJIT)
  8. Calculus I (NJIT)
  9. Trigonometry and Calculus (NJIT)
Bicycling, Hiking, Football (Soccer), Chess, and Running with my wife, Moira, our daughter Gracie, our son Jamie, and our dog Aurora (Australian Shepherd)
Entire Family   Entire Family   Me and MoGroupWedding

My main bike is a Surly Crosscheck that I take to various places.

Places I like to hike:
Breakneck Ridge (Bear Mountain)
Boroughs Range (Catskills: Slide Mountain, Cornell, Whitenberg)
Veerkerderkill Falls and Ice Caves (Sam's point)
Mount Tamany (Delaware Watergap)
Palisades (Shore trail + Great Steps)
Acadia National Park
Great Smokey Mountain National Park
Green Mountain National Forest
White Mountain National Forest

Some interesting places I have biked through:
Cycling around North Jersey

Here is a video of my bike commute:
Kearny to Newark

I used to play football in high school, and still try to play from time to time.  Now I'm more of a spectator, though.  I mostly follow the USMNT, Juventus, Liverpool, and Sheffield Wednesday.

Here's an album of the USMNT training session:

USMNT training 2011