Chapter 18 Introduction to machine learning
Machine learning (ML) is a tremendously popular method of gaining insights from data and to make predictions. It is somewhat distinct from artificial intelligence (AI) that we’ll discuss in Section 19.
18.1 What is machine learning
Machine learning is a way to automatically gain insights from data. Unlike analytical methods, such as graphs and tables, we did above, ML will “learn” from existing data with little user input, and based on the learned “knowledge” will either provide insights or make predictions. Traditionally, one tends to use the concept “machine learning” more often when making predictions, gaining insights is often just called statistics, analytics, or econometrics. But a large number of the methods overlap.
Also, the word “machine learning” is usually not used when talking about AI, large language models (LLM-s), and related methods. The name “ML” is typically reserved for “classical” ML methods.
Below I give only a brief intriduction and focus on predictions.
18.1.1 Supervised versus non-supervised methods
ML methods can be divided into two large categories: supervised methods and non-supervised methods, depending on whether you know what is the “correct” answer.
Supervised methods use data to predict the answer. Importantly, the “true answer” (often referred to as label) exists, although we may not know it. For instance, if you predict the students’ grade based on their first homework, or how long will a particular client be your cutomer are both examples of supervised learning. Even as we do not know the students’ grade, or the retention time for the customer right now, eventually there will be a “true” grade or “true” retention time.
Supervised models can be assessed based on how many predictions do they get right (see section 18.5). The more cases you get right, the better your model.
The \(k\)-NN method we discuss below is a supervised learnign method. Other popular methods include linear regression, decision trees and neural networks.
Unsupervised methods deal with cases where there is no “true” answer. A popular such method is clustering. Imagin a marketing department decides to use clustering to partition thousands of customers into three different groups. Their task is not to predict anything, but to manage a small number of marketing strategies–they can handle three different strategies, but not thousands. What is the best way to decide, which customer fits to which strategy?
Because there is no such thing as a true answer here–none of the customers walks around with marketing strategy label glued to their forehead. Hence we cannot even ask the questions like “did we get this customer right?”, and assessing the performance of non-supervised models requires different approaches.
Popular unsupervised methods include clustering and principal component analysis. On the simple end, you may count histograms and data plots as non-supervised ML methods; on the other end, the word embeddings that are fundamental tools for the large language models (LLM-s), are also constructed using unsupervised methods.
TBD: Data needed
- explanatory variables
- aka: exogenous variables, features, predictors, x-s…
- usually have many of these
- labels
- aka: endogenous variables, y-s..
- usually consider only one
18.1.2 Regression versus classification
Anothe important split runs between regression models and classification models. Both of these are supervised-type of learning where the “true” answer is of different type.
In case of regression, the label, the true answer is of numeric type. This includes income, education in years, probability the customer will leave, temperature tomorrow, and many other outcomes.
For classification or categorization, the outcome is categorical. For instance cat or dog, survived or died, cancer or no cancer, or one of a large number of college majors. In some sense the modern LLM-s belong to here too–based on your prompt and the previous words, they predict what the next word of the answer should be. So they predict one of many categories, word-by-word, and in this way come up with a textual answer.
In practice, both type of models are largely the same, and only require certain small twearks to work either for classification or regression. For instance, \(k\)-NN (see Section 18.3) can easily be adjusted for both tasks.
Below, we focus on classification tasks.
18.1.3 ML and AI
ML and AI are somewhat similar things.
- ML more precise and well defined.
- ML – same input, same output (mostly)
- AI – same input, different output
- ML: largely understand what’s going on, AI – we do not
- AI: easily 1,000,000 slower than ML, 1000 times more memory
- AI specific problems: hallucinations, biased language…
18.2 Decision boundary and decision boundary plot
It is very helpful to visualize classification tasks using decision boundaries and decision boundary plots. Take a look at the figure below. At left, it depicts a simple 2-dimensional dataset on \(x\)-\(y\) plane. Each datapoint belongs to one of the two classes–it is either a red cross or a green circle. But there two points where we do not know the class, labeled as gray “A” and “B”. The model’s task is to classify these two points. How would you do that?
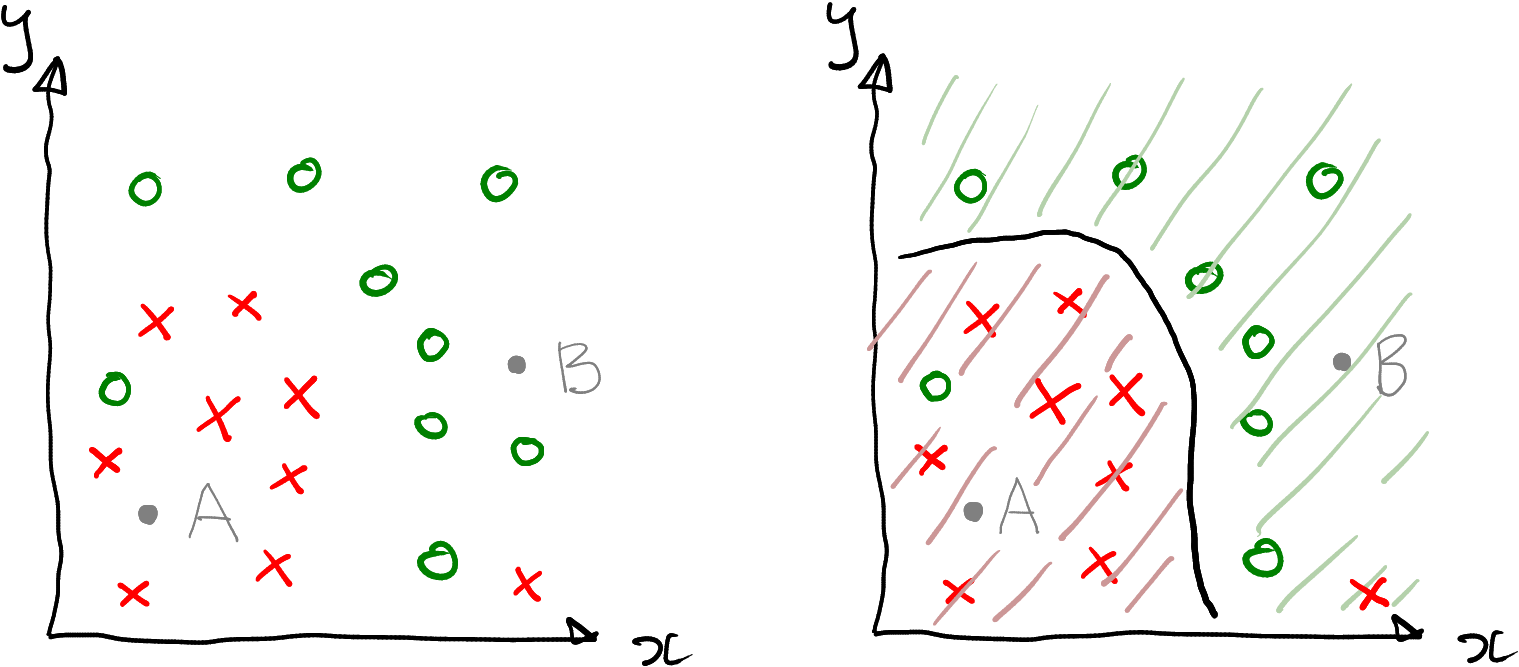
A simple 2-dimensional dataset where the task is to categorize data points into red crosses and green circles.
It would be natural to classify “A” as red and “B” as green–after all, “A” is located in a “red region” and “B” in a “green region”. Even more, it makes sense to classify all points at lower-left part of the figure as reds, and everything upper-right part of the figure as greens.
At right, this idea is formalized as decision boundary. This is the think black curve that separates the red and the green datapoints. We want to classify everything down-left of it as red, and everything up-right of it as red. The corresponding regions are marked with green and red stripes accordingly.
Not also that this boundary misses two points–there is one green circle in the red area, that would be mis-classified as red; and one red cross in the green area, that would be mis-classified as green. Decision boundary does not have to be precise–it just have to separate different kind of decisions (here either red or green). Decision boundary is specific to a model–different models, when trained on the given data, will result in different decision boundaries. In real applications we want to use a models that are as precise as possible–but we also do not want the models to overfit (see Section 18.6).
Decision boundary plots are very very useful to visualize and understand how the models work. However, these can only be used for 2-D datasets. In 3-D, you need to visualize complex boundaries in space that splits the space in regions of different color, the result will probably look great but incomprehensible. In higher dimensions, it is altogether impossible to visualize decision boundaries.
Next, I’ll demonstrate classifications using a simple and popular \(k\)-nearest neighbor method.
18.3 A method example: \(k\)-nearest neighbors
18.3.1 \(k\)-NN: the idea
The idea of \(k\)-nearest neighbors is simple: each datapoint will be categorized into the same group as its closest neighbors.
Look at the figure below. It displays a 2-D dataset with 9 datapoints, four reds, four greens, and one unknown (gray). If you pick the single closest neighbor (left), you would classify the unknown point as red, because its closest neighbor is red. This method is called nearest neighbors or 1-NN. However, if you pick three closest neighbors, it will have two green and one red neighbor. You would consider it to be green, as the two green dots “outvote” the single red (it is called majority voting). This method is called three-nearest-neighbor or 3-NN.
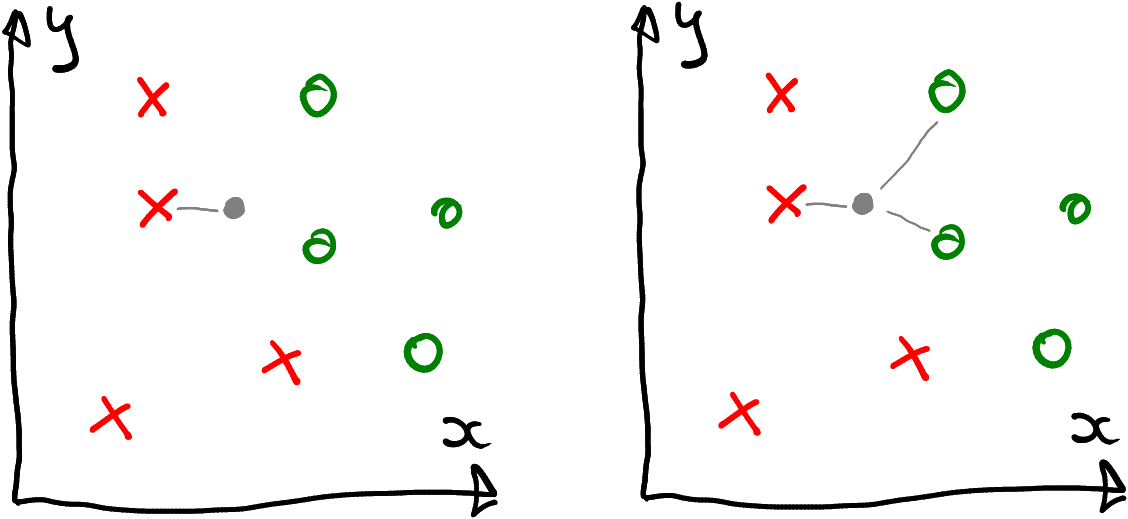
The unknown (gray) datapoint is classified as red based on the single closest neighbor, or as green if using three closest neighbors.
So the results of \(k\)-NN depend on the choice of \(k\). Normally you do not know what is its “correct” value (or more likely, the “best” value), it is something you have to figure out through modeling and testing. \(k\) is called hyperparameter, a parameter that is not interesting in terms of your results, but something you need to figure out in order to get the best results.
18.3.2 \(k\)-NN in R
Next, let’s demonstrate how to use \(k\)-NN in R using yin-yang data.

For a quick overview, let’s first plot the data. As the color c is coded as a number (0/1), I turn it into a factor for better plotting. It is also required later for \(k\)-NN.
yinyang <- read_delim(
"data/yin-yang.csv.bz2") %>%
mutate(c = factor(c))
yinyang %>%
ggplot(aes(x, y, col = c)) +
geom_point() +
coord_fixed() +
theme(legend.position = "none")The plot displays datapoints of two colors, arranged somewhat in Yin-Yang pattern. Not also that the boundary between the dots is not quite clear but includes some blues “trespassing” into the red area and the way around. Obviously, the decision boundary should run broadly follow the curved blue-red boundary line.
Next, it is time to use \(k\)-NN to make predictions. Here we use
class library. The important function in the library is the
function knn(train, test, cl, k). The arguments are:
- train: training data. This is the set of datapoints where we know the correct color, currently either red or blue (“0” or “1”).
- test: validation data. These are the datapoints, color of which is to be predicted. These are either the points where we do not know the color and want to use the model to predict it, or maybe the points where we still know the correct value, but we want to check (validate) how well does the do in terms of getting the correct values.
- cl: classes. These are the known color values that correspond to the train datapoints.
- k: number of neighbors to consider.
library(class)
X <- yinyang %>%
select(x, y)
y <- yinyang$c
data <- data.frame(x = -2:2, y = 2:-2)
yhat <- knn(X, data, cl = y, k = 1)
data$c <- yhat
yinyang %>%
ggplot(aes(x, y, col = c)) +
geom_point() +
coord_fixed() +
geom_point(data = data, pch = 1, size = 2)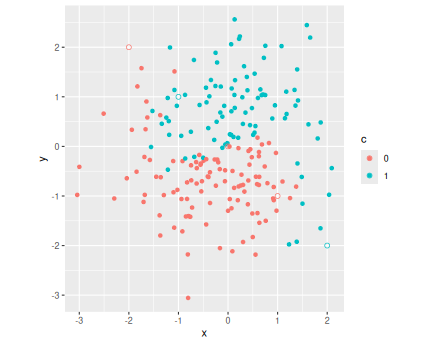
18.4 \(k\)-NN decision boundary
ex <- seq(min(X$x), max(X$x), length.out = 50)
ey <- seq(min(X$y), max(X$y), length.out = 50)
grid <- merge(ex, ey)
grid$c <- knn(X, grid, y, k = 1)
ggplot(grid, aes(x, y)) +
geom_tile(data = grid,
aes(fill = c),
alpha = 0.35) +
geom_point(data = yinyang,
aes(col = c),
size = 0.5) +
theme(legend.position = "none") +
coord_fixed()
DBPlot <- function(Xt, yt, Xv, yv, k = 1, nGrid = 100) {
ex <- seq(min(train$x), max(train$x), length.out=nGrid)
ey <- seq(min(train$y), max(train$y), length.out=nGrid)
grid <- merge(ex, ey)
grid$yhat <- knn(Xt, grid, yt, k = k)
Xv$c <- yv
ggplot(grid) +
geom_tile(data = grid,
aes(x, y, fill = yhat),
alpha = 0.3) +
geom_point(data = Xv,
aes(x, y, col = factor(c)),
size = 0.5) +
theme(legend.position = "none") +
coord_fixed()
}
# DBPlot(Xt, yt, Xt, yt, 1)18.5 Confusion matrix
18.6 Overfitting and validation
if \(k=1\) overfits:
## y
## yhat 0 1
## 0 109 0
## 1 0 91Need data the model hasn’t seen. Split into training/testing parts:
Train on training data, evaluate on validation data:
## yv
## yvhat 0 1
## 0 24 0
## 1 1 15## [1] 0.975## yt
## ythat 0 1
## 0 84 0
## 1 0 76## [1] 1Which \(k\) will give you best validation accuracy?