Chapter 15 The gglot2 Library
Data visualizations (plotting) is one of the most powerful ways to
communicate information and findings.
R provides
multiple visualization packages, in particular the base-R plotting
tools (the graphics library) which is flexible and powerful.
However, in this chapter we introduce ggplot2 library that is
oriented to visualizing datasets. It has intuitive and powerful
interface and simplifies many tasks that are tedious to achieve with
base-R graphics. But be aware that as other tools, so also ggplot2
has its limits, and sometimes it is better to use other visualization
packages.
ggplot2 is called ggplot2 because once upon a time there was a package called ggplot. However, as the authors found its API somewhat limiting, they wanted to break compatibility and start from blank sheet. To distinguish the new package from the old one, they called it ggplot2.
Examples in this chapter adapted from R for Data Science by Garrett Grolemund and Hadley Wickham.
15.1 A Grammar of Graphics
Just as the grammar of language helps us construct meaningful sentences out of words, the Grammar of Graphics helps us to construct graphical figures out of different visual elements. This grammar gives us a way to talk about parts of a plot: all the circles, lines, arrows, and words that are combined into a diagram for visualizing data. Originally developed by Leland Wilkinson, the Grammar of Graphics was adapted by Hadley Wickham to describe the components of a plot, including
- the data being plotted
- the geometric objects (circles, lines, etc.) that appear on the plot
- the aesthetics (visual appearance) of the geometric objects that makes up the plot. It also covers the mapping how the visual appearance of those aesthetics is related to data variables.
- a statistical transformation used to calculate the data values used in the plot
- a position adjustment for locating each geometric object on the plot
- a scale (e.g., range of values) for each aesthetic mapping used
- a coordinate system used to organize the geometric objects
- the facets or groups of data shown in different plots
Wickham further organizes these components into layers, where each layer has a single geometric object, statistical transformation, and position adjustment. Following this grammar, you can think of each plot as a set of layers of images, where each image’s appearance is based on some aspect of the data set.
All together, this grammar enables you to discuss what plots look like using a standard set of vocabulary. And like with dplyr and the Grammar of Data Manipulation, ggplot2 uses this grammar directly to declare plots, allowing you to more easily create specific visual images.
The ggplot2 library provides a set of declarative functions that mirror the above grammar, enabling you to easily specify what you want a plot to look like (e.g., what data, geometric objects, aesthetics, scales, etc. you want it to have).
ggplot2 is another external package (like stringr and readr), so
you may need to install (using install.packages("ggplot2") and load
it with:
However, it is also a part of tidyverse set of packages, so if you installed and loaded tidyverse, then ggplot2 is ready to use.
15.2 Basic Plotting with ggplot2
15.2.1 mpg data
ggplot2 library comes with a number of built-in data sets. One of the most popular of these is mpg, a data frame about fuel economy for different cars. It is a sufficiently small but versatile dataset to demonstrate various aspects of plotting. mpg has 234 rows and 11 columns. Below is a sample of it:
## # A tibble: 3 × 11
## manufacturer model displ year cyl trans drv cty hwy
## <chr> <chr> <dbl> <int> <int> <chr> <chr> <int> <int>
## 1 pontiac grand prix 5.3 2008 8 auto(s4) f 16 25
## 2 toyota toyota tacoma 4wd 4 2008 6 auto(l5) 4 16 20
## 3 toyota 4runner 4wd 4.7 2008 8 auto(l5) 4 14 17
## fl class
## <chr> <chr>
## 1 p midsize
## 2 r pickup
## 3 r suvThe most important variables for our purpose are following:
- class, car class, such as SUV, compact, minivan
- displ, engine size (liters)
- cyl, number of cylinders
- hwy, mileage on highway, miles per gallon
- manufacturer, producer of the car, e.g. Volkswagen, Toyota
15.2.2 Our first ggplot
In order to create a plot, you call the ggplot() function, specifying the data that you wish to plot. You then add new layers that are geometric objects which will show up on the plot:
# plot the `mpg` data set, with highway mileage on the x axis and
# engine displacement (power) on the y axis:
ggplot(data = mpg) +
geom_point(mapping = aes(x = displ, y = hwy))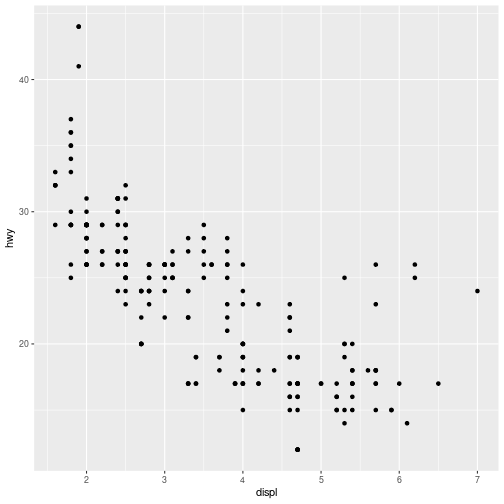
plot of chunk basic_mpg
To walk through the above code:
The
ggplot()function is passed the data frame to plot as thedataargument.You specify a geometric object (
geom) by calling one of the manygeomfunctions, which are all namedgeom_followed by the name of the kind of geometry you wish to create. For example,geom_point()will create a layer with “point” (dot) elements as the geometry. There are a large number of these functions; see below for more details.For each
geomyou must specify the aesthetic mappings, which is how data from the data frame will be mapped to the visual aspects of the geometry. These mappings are defined using theaes()function. Theaes()function takes a set of arguments (like a list), where the argument name is the visual property to map to, and the argument value is the data property to map from.Finally, you add
geomlayers to the plot by using the addition (+) operator.
Thus, basic simple plots can be created simply by specifying a data set, a geom, and a set of aesthetic mappings.
- Note that
ggplot2library does include aqplot()function for creating “quick plots”, which acts as a convenient shortcut for making simple, “default”-like plots. While this is a nice starting place, the strength ofggplot2is in it’s customizability, so read on!
15.2.3 Aesthetic Mappings
The aesthetic mapping is a central concept of every data visualization. This means setting up the correspondence between aesthetics, the visual properties (visual channels) of the plot, such as position, color, size, or shape, and certain properties of the data, typically numeric values of certain variables. Aesthetics are the representations that you want to drive with your data properties, rather than fix in code for all markers. Each visual channel can therefore encode an aspect of the data and be used to express underlying patterns.
The aesthetics mapping is specified in the aes() function call in the geom layer. Above we used mapping aes(x=displ, y=hwy). This means to map variable displ in the mpg data (engine size) to the horizontal position (x-coordinate) on the plot, and variable hwy (highway mileage) to the vertical position (y coordinate). We did not specify any other visual properties, such as color, point size or point shape, so by default the geom_point layer produced a set of equal size black dots, positioned according to the date. Let’s now color the points according to the class of the car. This amounts to taking an additional aesthetic, color, and mapping it to the variable class in data as color=class. As we want this to happen in the same layer, we must add this to the aes() function as an additional named argument:
# color the data by car type
ggplot(data = mpg) +
geom_point(mapping = aes(x = displ, y = hwy, color = class))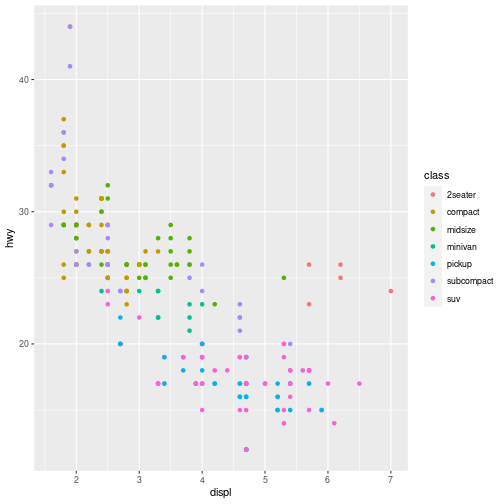
plot of chunk aes_color
(ggplot2 will even create a legend for you!)
Note that using the aes() function will cause the visual channel to be based on the data specified in the argument. For example, using aes(color = "blue") won’t cause the geometry’s color to be “blue”, but will instead cause the visual channel to be mapped from the vector c("blue")—as if you only had a single type of engine that happened to be called “blue”:
ggplot(data = mpg) + # note where parentheses are closed
geom_point(mapping = aes(x = displ, y = hwy, color = "blue"))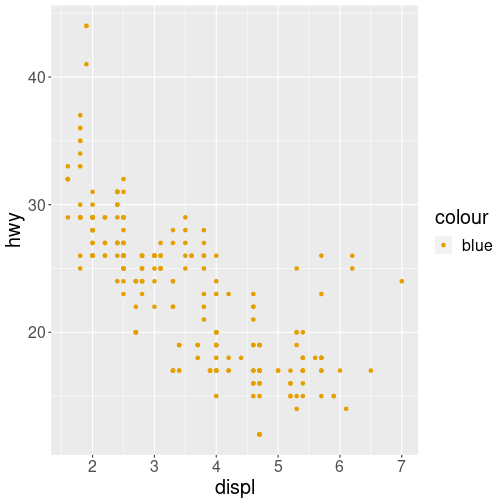
plot of chunk wrong_blue
This looks confusing (note the weird legend!) and is most likely not what you want.
If you wish to specify a given aesthetic, you should set that property as an argument to the geom method, outside of the aes() call:
ggplot(data = mpg) + # note where parentheses are closed
geom_point(mapping = aes(x = displ, y = hwy), color = "blue") # blue points!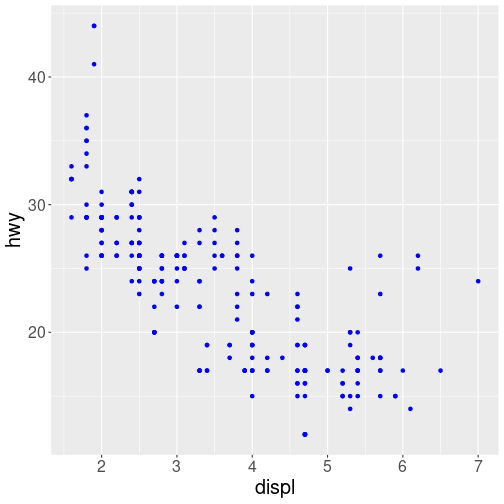
plot of chunk color_blue
15.2.4 Specifying Geometry
The most obvious distinction between plots is what geometric objects (geoms) they include. ggplot2 supports a number of different types of geoms, including:
geom_pointfor drawing individual points (e.g., a scatter plot)geom_linefor drawing lines (e.g., for a line charts)geom_smoothfor drawing smoothed lines (e.g., for simple trends or approximations)geom_barfor drawing bars (e.g., for bar charts)geom_polygonfor drawing arbitrary shapes (e.g., for drawing an area in a coordinate plane)geom_mapfor drawing polygons in the shape of a map! (You can access the data to use for these maps by using themap_data()function).
Each of these geometries will need to include a set of aesthetic mappings (using the aes() function and assigned to the mapping argument), though the specific visual properties that the data will map to will vary. For example, you can map data to the shape of a geom_point (e.g., if they should be circles or squares), or you can map data to the linetype of a geom_line (e.g., if it is solid or dotted), but not vice versa.
- Almost all
geomsrequire anxandymapping at the bare minimum.
# line chart of mileage by engine power
ggplot(data = mpg) +
geom_line(mapping = aes(x = displ, y = hwy))
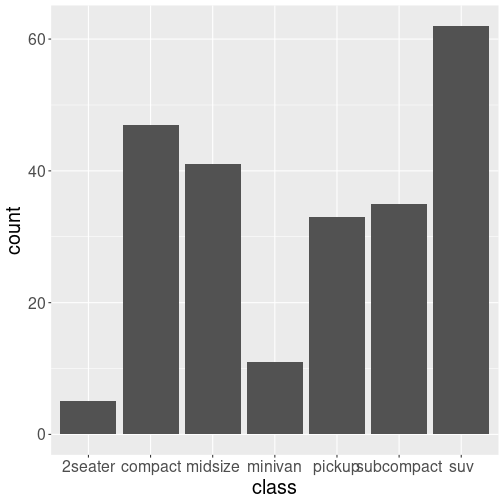
# bar chart of car type
ggplot(data = mpg) +
geom_bar(mapping = aes(x = class)) # no y mapping needed!
What makes this really powerful is that you can add multiple geometries to a plot, thus allowing you to create complex graphics showing multiple aspects of your data
# plot with both points and smoothed line
ggplot(data = mpg) +
geom_point(mapping = aes(x = displ, y = hwy)) +
geom_smooth(mapping = aes(x = displ, y = hwy))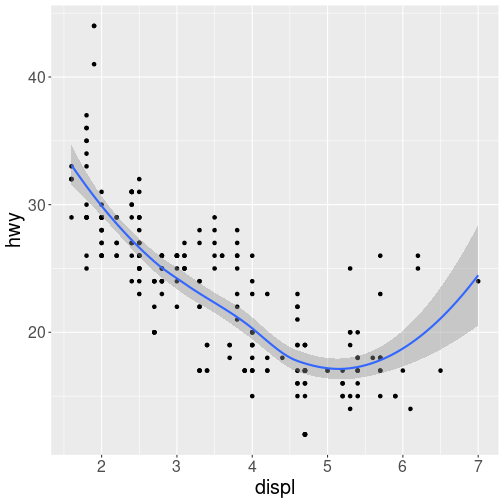
plot of chunk multi_geom
Of course the aesthetics for each geom can be different, so you could show multiple lines on the same plot (or with different colors, styles, etc). It’s also possible to give each geom a different data argument, so that you can show multiple data sets in the same plot.
- If you want multiple
geomsto utilize the same data or aesthetics, you can pass those values as arguments to theggplot()function itself; anygeomsadded to that plot will use the values declared for the whole plot unless overridden by individual specifications.
15.3 Most important plot types
15.3.1 Scatterplot
On of the most widely used plot type is scatterplots, plots of point clouds.
An example scatterplot of random data.
Scatterplots are good to visualize continuous data–it is best if the variable you put both on the horizontal and vertical axis are continuous. This includes values like income and age, usage percentage and versus reliability, and GDP and child mortality.
Second, it the objects you put on the plot should be distinct, and that should not be a transition path from one to another. So different humans, hard disks or countries are good examples–one human does not transform into another, and neither do hard disks. Even for countries, such transitions are very rare.
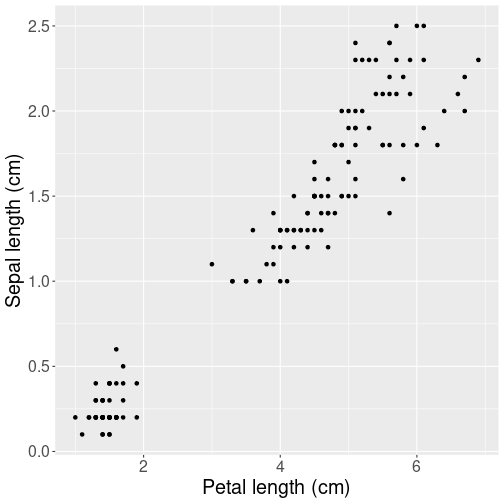
Petal length versus width for iris flowers.
Here is an example scatterplot of real data–of the R built-in iris dataset:
The plot depicts the relationship between length and width of petals of iris flowers. Scatterplot is a good choice here because each unit (observation) in data depics a separate flower. Obviously, flowers do not transition to each other, so it would be misleading (and very ugly) to connect the dots. We prefer a scatterplot.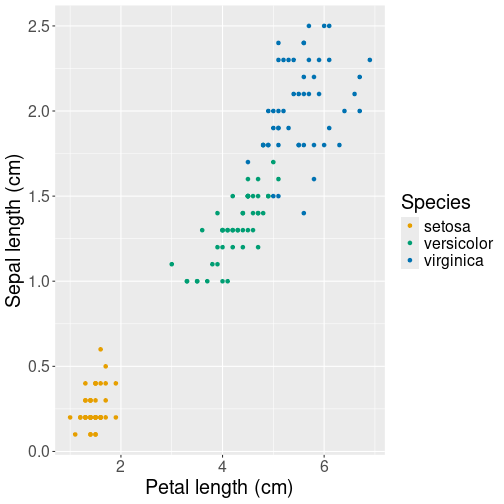
Petal length versus width for iris flowers, this time marking different species with different colors.
However, there are three different species included in the dataset. If we want to convey the difference of their petal size, we can use another aesthetic, for instance color, to represent species:
Additional aesthetics allow to represent more information, besides of the relationship we can also see that setosa flowers tend to be small and virginica flowers large.15.3.2 Line plot
Line plot is another very popular way of presenting information. It is similar to scatterplot in a sense that it is well-suited for plotting continuous data. However, connecting points with lines is useful mainly if there is a clear transition from one observation to the next one. This is commonly the case with time series data–time flows continuously, and usually the features we measure at different point of time are also continuously changing.
We demonstrate line plot using Scandinavian COVID-19 data:
covS <- read_delim("data/covid-scandinavia.csv.bz2") %>%
select(country, date, type, count) %>%
filter(date > "2020-03-01",
date < "2020-07-01")
# select a 4-month date range only
covS %>%
sample_n(5)## # A tibble: 5 × 4
## country date type count
## <chr> <date> <chr> <dbl>
## 1 Sweden 2020-03-30 Deaths 332
## 2 Finland 2020-04-21 Deaths 141
## 3 Finland 2020-04-04 Deaths 25
## 4 Finland 2020-06-18 Confirmed 7119
## 5 Sweden 2020-06-18 Deaths 5270The dataset includes the cumulative number of deaths and confirmed cases in four Scandinavian countries, Norway, Sweden Denmark and Finland. Note the structure of the dataset: an observation is country-date-type combination. For each country and each date, there are types of counts: Deaths and Confirmed. Below, we filter deaths only.
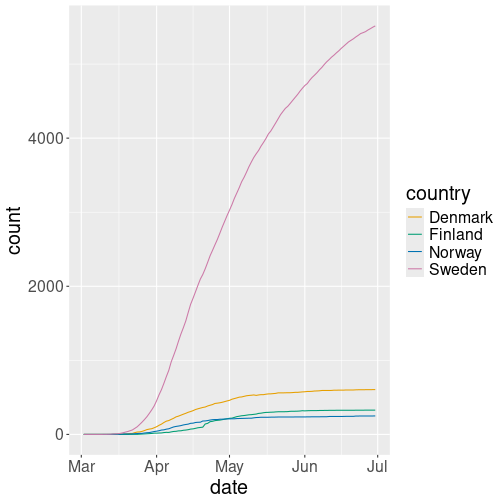
Line plot of total COVID-19 deaths. Different countries are depicted by different color.
As the data contains four different countries, it is a natural way to
distinguish between countries using lines of different color: we pick
the color aesthetic and map it to variable country: col = country:
covS %>%
filter(type=="Deaths") %>%
# look at deaths only
ggplot(aes(date, count,
# date vs death count
color=country)) +
# distinguish countries by color
geom_line() +
theme(text = element_text(size=15))
# make text largerThe data shows that there was a rapid growth in COVID-19–related deaths in spring 2020. We can also see that there were many more deaths in Sweden than elsewhere.
Why is line plot a good choice here? Because the counts are based on dates, and time flows continuously from one day to another. One can imagine replacing the lines by dots (scatterplot), and sometimes it is useful. But here lines stress that observations–the dots–are actually connected. As time flows, yesterday turns into today, and yesterday’s counts turn into today’s counts.
Denoting different countries with similar lines.
Sometimes we may not want to use different colors or linestyles to denote different countries (or other groups of observations). In that case one can use the group aesthetic–it simply tells which observations should be grouped together. Visual representation, however, is unaffected:
covS %>%
filter(type=="Deaths") %>%
ggplot(aes(date, count,
group=country)) +
# denote different countries by different lines
# of same color and type
geom_line(col="gray") +
theme(text = element_text(size=15))The plot is less attractive, and, in particular, we cannot tell which line represents which country. But this may be sometimes desirable, for instance, if there are too many groups to color them individually. We may want to plot everything with the same gray color, and add a selected few with marked colors on top of it.
Unsuccessful attempt to do ungrouped line plot.
However, if you leave out group or color attribute alltogether, then the result may be hard to interpret:
covS %>%
filter(type=="Deaths") %>%
ggplot(aes(date, count)) +
geom_line() +
theme(text = element_text(size=15))What happens here is that ggplot orders the observations along the date-axis, and then uses line to connect previous count to the next count. However, for every day we have four different counts–one for each country. So it ends up connecting all countries vertically for each date, and so we get an interesting shape made of densely packed lines here.
15.3.3 Barplot
Barplots are suitable to display data where one variable is categorical and the other one is numerical. We demonstrate the barplot using the average size of orange trees (see Section 11.2):
avg <- Orange %>%
group_by(Tree) %>%
summarize(size = mean(circumference))
avg # average size of 5 orange trees## # A tibble: 5 × 2
## Tree size
## <ord> <dbl>
## 1 3 94
## 2 1 99.6
## 3 5 111.
## 4 2 135.
## 5 4 139.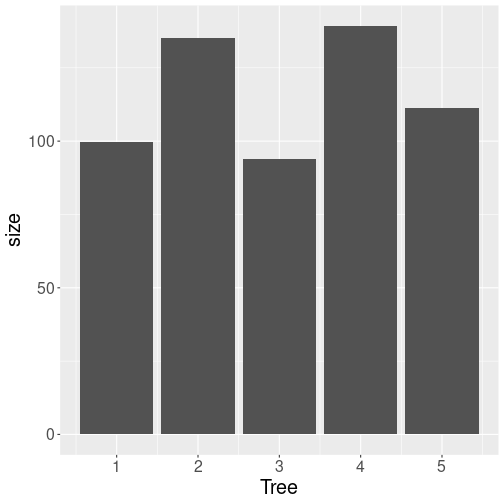
Barplot using default options.
For instance, we can plot
Barplots can be created with geom_col() (there is also geom_bar()
but that creates histograms by default!)
The default options of geom_col() create
a rather dull figure of gray bars, but it conveys all the
necessary information.
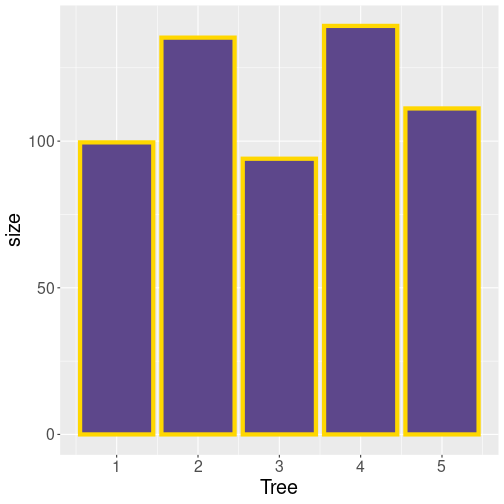
Adjusting colors of barplot. Remember that fill is the fill color and col is the border color. size here is the width of the outline.
The gray color may be exactly what you want if you intend to print it on b/w printer. But if you want to show it on a color-aware device, you may want to specify colors:
Why is barplot a good plot type for such tasks? This is because the horizontal position of bars is rather arbitrary (often based on alphabetic ordering, here based on the average size of trees). Bars are just next to each other, they are typically also of equal width, and the fact that tree “3” is after tree “2” does not typically mean these trees are “close” in any meaningful sense. The discrete bars stress that there is no natural smooth connection between trees, they are separate discrete .
Exercise 15.1 Color each bar of different color by making the fill aesthetic to depend on the tree id. Do you like the result?
See the solution
15.4 Most important plot proporties
It is important to know how to produce the desired plots on computer. But it is perhaps even more important to know what kind of plots to produce. Here we discuss some of the most important properties you should try to achieve.
15.4.1 Linear and log scale
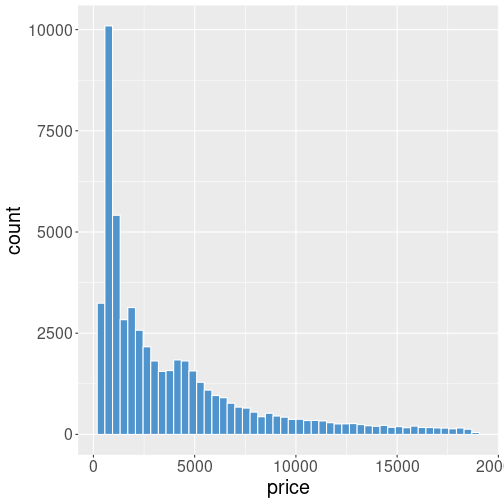
Diamonds’ price. Both the horizontal and vertical axes are in linear scale.
Many datasets contain a lot of small values and not so many large values. For instance, the histogram of diamond’s price will look like
This may be exactly what you want–it shows that there are many cheap diamonds (in a few thousand dollar price range), and not that many expensive ones with a price over $10,000. But this plot also has it’s downsides–only a small portion of the figure is devoted to the most common price range, while over a half of it is almost empty, and confirming what we may know anyway–there are not that many expensive gems.
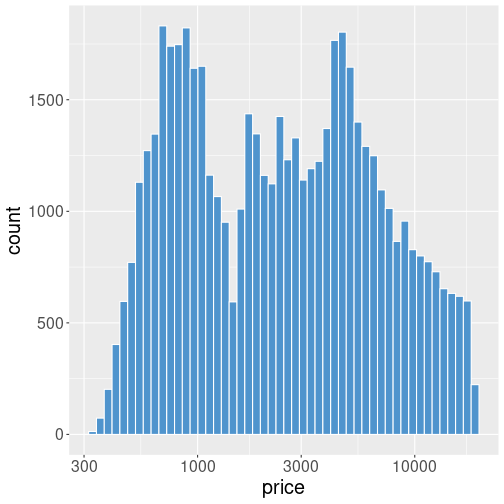
Diamonds’ price. The vertical axis is still linear, but the horizontal is now in log scale. It is a log-linear plot.
Let’s repeat the above example using log scale:
ggplot(diamonds, aes(price)) +
geom_histogram(bins=50,
fill="steelblue3",
col="white") +
scale_x_log10()Code-wise, we just add + scale_x_log10() to the previous example,
this forces the x-axis to be logarithmic.
(See Section 15.5.4 for more about scales).
Now the plot looks very different. The bars are of broadly equal
height and a problem with the previous plot–a lot of empty space–is
gone.
15.5 Tuning Your Plots
As you noticed, ggplot2 can be used to build a large variety of
plots. ggplot will also supply meaningful labels, and pick
appropriate colors, so you immediately have something that looks
reasonable so you can present it right away.
But unfortunately, even if reasonable, the resulting plot may not be good enough. Sometimes you are happy with the fonts and colors and want just to adjust the labels, but other times the colors are completely misleading and the plot looks like an incomprehensible mish-mash. There is no way around to tuning the plots.
15.5.1 Adjusting colors
One of the most common things we want to adjust are colors. We
discussed above how you can specify colors manually (e.g. as
geom_point(col = "black")), or through aesthetic mapping (e.g. as
geom_point(aes(col = elevation)).
It is often possible to specify each color manually, but first let’s
look how to do it using color scales.
The general way of tuning colors is by using scales. While aesthetic mapping tells which visual properties will be mapped to which data variable, scales tell how this mapping should be done. For instance, when we map color to elevation, then we can choose high elevation to be displayed as white, and negative values are deep blue. But we can also pick a different color scheme, e.g. high elevations as yellow and low as red. Such choices–which colors represent which values in data–are done through scales.
15.5.1.1 Discrete colors
Consider a simple task: you are political analyst in India and you want to produce a plot of election results–the number of seats in Lok Sabha (the lower house) won by the three largest parties, BJP (Bharatiya Janata Party), INC (Indian National Congress) and AITC (All India Trinamool Congress). You have a data frame that looks like:
## party seats
## 1 BJP 303
## 2 INC 52
## 3 AITC 23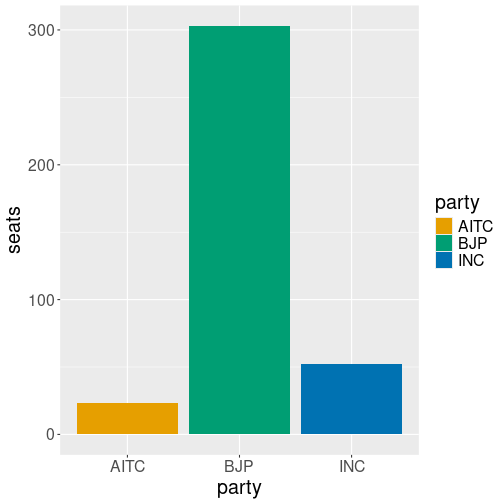
Seats by political parties using default colors.
It is easy to visualize the results with colored bars:
But we have a problem–the political parties traditionally are represented with colors, but just not with these colors. BJP is usually saffron (orange), INC is sky blue, and AITC is light green. The colors here are just misleading.
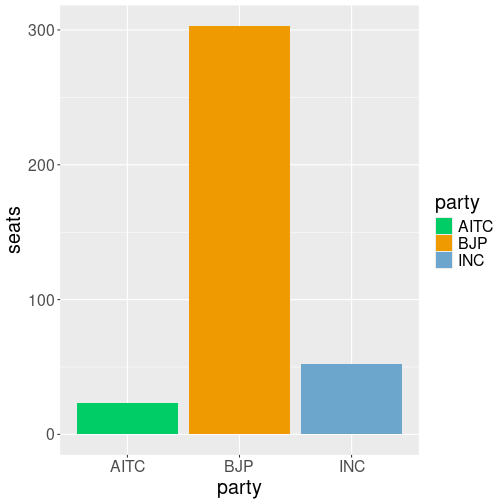
Seats by political parties represented by custom colors.
Fortunately, the solution is easy. We need to add a color scale,
that tells which party name should correspond to which color. This
can be achieved by scale_fill_manual(values = c(BJP="orange2", ...)):
ggplot(data,
aes(party, seats, fill=party)) +
geom_col() +
scale_fill_manual(
values = c(BJP="orange2",
INC="skyblue3",
AITC="springgreen3")
)This results in the desired colors for each political party.
Note the syntax of setting colors:
scale_fill_manual takes argument values, and that is a named
vector where names correspond to the discrete values of the variable
(here party) and the vector components are the corresponding color
values. Obviously, one can also use different color codes, such as
c(BJP="#FF9933", INC="#19AAED", AITC="#20C646") for somewhat more
customary colors for these parties.
Exercise 15.2 What happens if you use scale_fill_manual() but do not specify the
color for one of the discrete value? Do you get an error, a default
color, or something else? Try it with the political party plot!
But now we need to talk a few more words about scale_fill_manual().
What exactly does it do and when should you use it?
fillinscale_fill_manualmeans you manually specify individual colors for the fill aesthetic. If you usecol = partyinstead offill = party, then you need to use its sibling function,scale_color_manual()instead.manualmeans that you can only specify colors for discrete values. Normally there should not be that many different values–from two till maybe 10 are reasonable, although in principle, there are no limits–if you have dozens of different color codes for different values, then you can specify those.If the data variable is not discrete, e.g. you want to specify colors for different years, but year is a continuous number, then
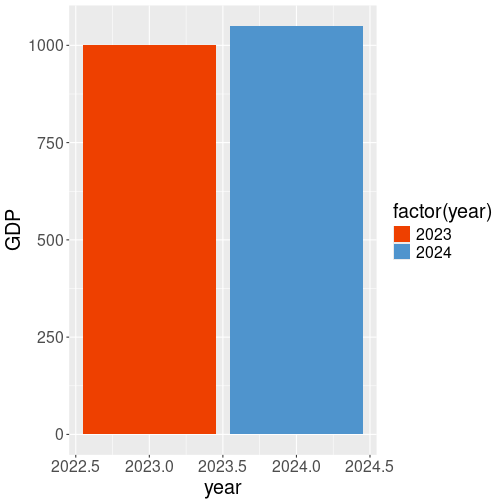
scale_fill_manual()will not work. You get an errordata.frame(GDP=c(1000, 1050), year=c(2023, 2024)) %>% ggplot(aes(year, GDP, fill=year)) + geom_col() + scale_fill_manual( values = c("2023"="orangered2", "2024" = "steelblue3") )## Error: Continuous value supplied to discrete scale The error tells you exactly what it is–a continuous value (here
year) is supplied to a discrete scale (here
The error tells you exactly what it is–a continuous value (here
year) is supplied to a discrete scale (here
scale_fill_manual()).If different discrete colors for different years is what you want, then you have to force year to be discrete by wrapping it in
factor():data.frame(GDP=c(1000, 1050), year=c(2023, 2024)) %>% ggplot(aes(year, GDP, fill=factor(year))) + geom_col() + scale_fill_manual( values = c("2023"="orangered2", "2024" = "steelblue3") )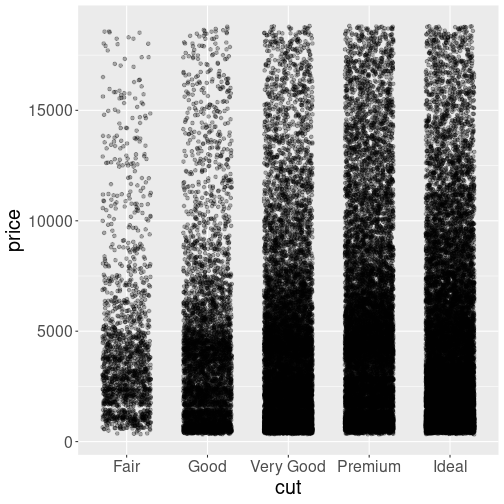 (See more in Section 10.7.)
(See more in Section 10.7.)
15.5.1.2 Continuous colors
To specify individual colors manually is a good choice when there is only a small number of discrete data values. But often we have data where the count of possible values is essentially unlimited. This includes many physical measurements, such as height, weight, temperature, elevation and light intensity. Also many economic measures, in particular those that involve money belong here–income, wealth, price and GDP, but also inflation and unemployment are such values. In such a case there is no way that we can specify the colors manually. We need a continuous scale for continuous variables.
Below, we use Icecream dataset from Ecdat package (see Section 6.5 for how to install and load packages). This is a small dataset of ice cream consumption in the U.S. in the early 1950s, a sample of data looks like:
## cons income price temp
## 20 0.342 86 0.277 60
## 8 0.288 79 0.267 47
## 3 0.393 81 0.277 63
## 4 0.425 80 0.280 68
## 30 0.548 90 0.260 71here cons is ice cream consumption (per person in pints), income is average family income (USD per week), price is USD per pint, and temperature is in °F.
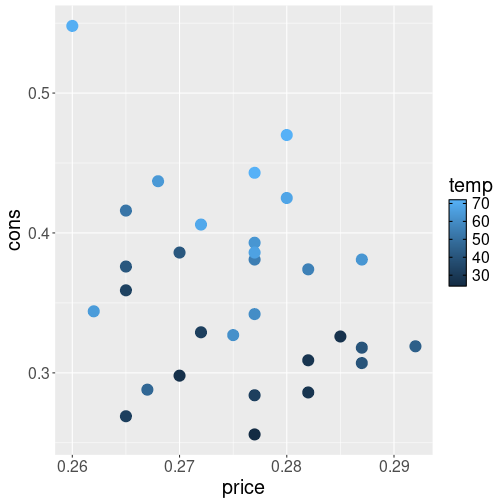
We can make a simple plot about how consumption depends on price and temperature as
ggplot(Ecdat::Icecream,
aes(price, cons, col=temp)) +
geom_point(size=5) +
theme(text = element_text(size=16))The picture suggests that there is little relationship between price and consumption (the dots are arranged fairly randomly). However, the relationship between weather and consumption is strongly related–as you see the light blue colors, denoting warmer weather, tend to be associated with more consumption.
In terms of colors, ggplot will pick a scale from dark blue (low values) to light blue (high values) to represent the various temperature values. This is a continuous color scale, a color gradient, and it can represent unlimited number of colors, corresponding to unlimited number of potential temperature values.
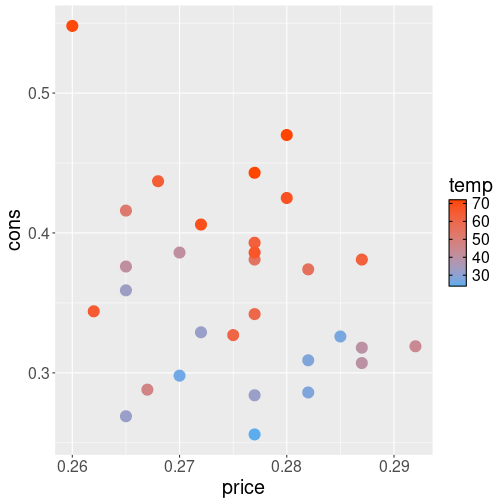
But in case of cold and hot weather, we may want to show the
temperature not just in shades of blue, but use, e.g. reds to
represent hot and blue to represent cold weather. If this is what we
want, we need to supply our own custom color gradient values. This
can be done with scale_color_gradient(low="blue", high="red"). This
will make a similar color gradient from blue, representing the lowest
value in data, to red that represent the highest value in data:
ggplot(Ecdat::Icecream,
aes(price, cons, col=temp)) +
geom_point(size=5) +
scale_color_gradient(
low="steelblue2",
high="orangered2"
) +
theme(text = element_text(size=16))The message from the image is similar but the choice of colors is a more conventional one when representing temperatures.
Please note that scale_color_gradient() is the right scale to use if
you use the color aesthetic. If you use fill instead, then you
should pick scale_fill_gradient().
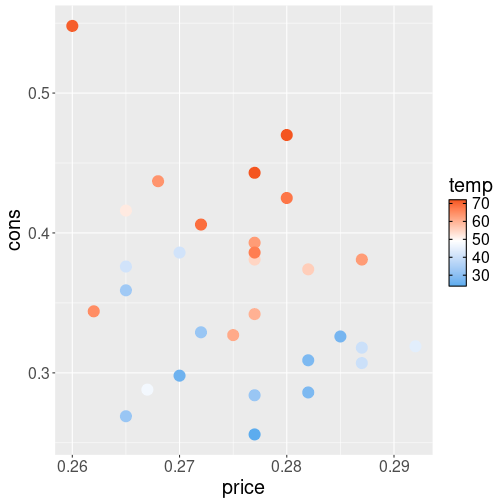
There are more ways to create gradients. For instance, if you want
the blues not to turn into reds directly, but first into white, and
thereafter into red, then you can use use scale_color_gradient2().
That one takes three color values: low, mid and high, it also
requires the midpoint value midpoint–what is the middle temperature value that
should be represented as the middle color:
midpoint <- mean(Ecdat::Icecream$temp)
ggplot(Ecdat::Icecream,
aes(price, cons, col=temp)) +
geom_point(size=5) +
scale_color_gradient2(
low = "steelblue2",
mid = "white",
high = "orangered2",
midpoint = midpoint
) +
theme(text = element_text(size=16))Here we picked the middle point value to be mean temperature in the data.
If just two gradients with a middle point is still too little for you
then check out scale_color_gradientn() and pre-defined
palettes below.
In a similar fashion like the discrete manual scale (see Section 15.5.1.1), continuous scale fails if fed with discrete data. If we try to use color gradient with the political parties example above in Section 15.5.1.1, we get:
partySeats <- data.frame(party = c("BJP", "INC", "AITC"),
seats = c(303, 52, 23))
ggplot(partySeats,
aes(party, seats, fill=party)) +
geom_col() +
scale_fill_gradient()## Error: Discrete value supplied to continuous scaleThis means that the scale is expecting all kinds of numbers, put it
was fed with fill=party, and party only contains discrete values.
15.5.1.3 Pre-defined palettes
It is fairly easy to pick two-three colors that fit nicely together
and get a professional-looking plot in this manner. But if you want
to pick a larger number of colors, then it will rapidly become
tricky. The task gets even more complex if you intend your figures to
be readable for people with different types of color-blindness, or
when printed on a paper in just black and white. Fortunately, you are
not the first one who stumbles upon this problem. R includes a number
of pre-defined color palettes. These include
heat.colors(), terrain.colors(),
topo.colors() and others. These functions return a number of color
codes, e.g.
## [1] "#FF0000" "#FF8000" "#FFFF00" "#FFFF80"returns four color codes on red-yellow scale that may be good to represent “heat”.
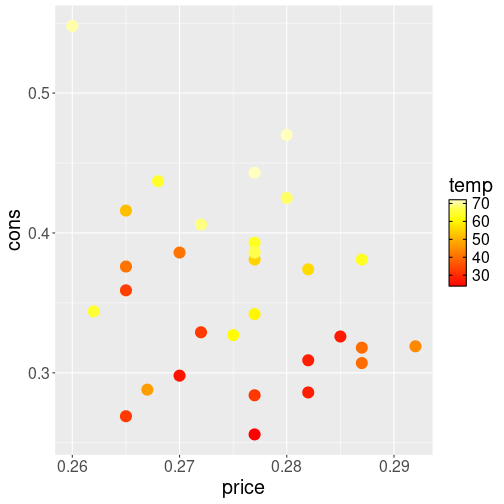
Icecream consumption versus price. Outside temperature marked using
heat.colors().
If we
want to use such palettes for ggplot gradients then we can just feed
a number of color from the palette to scale_color_gradientn():
ggplot(Ecdat::Icecream,
aes(price, cons, col=temp)) +
geom_point(size=5) +
scale_color_gradientn(
colors=heat.colors(10)
) +
theme(text = element_text(size=16))The result looks like different levels of heat, although the color codes may be more about melting steel and less about weather…
These palettes above are designed with a continuous data in mind, like the smooth transition of color with temperature above. If you are displaying discrete values, then you may prefer colors that are the opposite–not blending smoothly into each other but easy to distinguish instead. ggplot2 includes such a palette, e.g. the default colors for election results in Section 15.5.1.1 are selected from the ggplot’s built-in palette.
Another popular choice
is to use a pre-defined palette from
colorbrewer.org. Color brewer
palettes have been designed to look good and to be viewable both for
people with normal vision and also with certain forms of color
blindness. Colorbrewer’ color palettes are incorporated into R’s
RColorBrewer package, one can see all the palettes with
RColorBrewer::display.brewer.all()14
(but remember to install
RColorBrewer() first).
You can also get the palette and it’s color codes
colorbrewer website by looking at the
scheme query parameter in the URL.
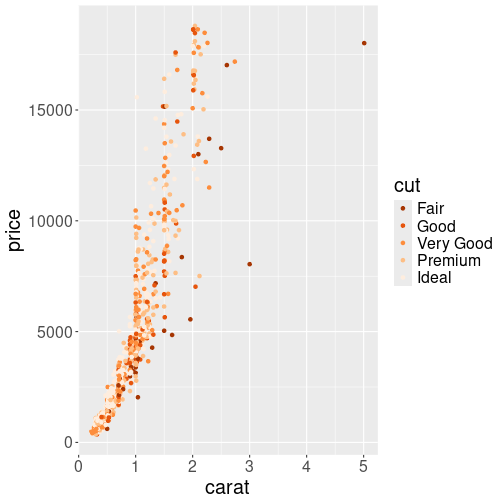
1000 random diamonds’ size versus price, with cut denoted by different oranges.
These palettes can be used with scale_color_brewer() function,
passing the palette as an argument. For instance, let’s plot the
diamonds price using “Accent” palette:
diamonds %>%
sample_n(1000) %>%
ggplot(aes(carat, price, col=cut)) +
geom_point() +
scale_color_brewer(palette = "Oranges",
direction = -1)The last argument, direction = -1, reverses the scale, so “Fair”
fill be dark and “Ideal” light orange.
Note that ColorBrewer’s palettes are discrete–even the
continuous–looking scales, like “YlOrRd” (yellow-orange-red) or
“Blues” (light blues to dark blues) are discrete scales with only a
limited number of possible values. This is because the human eye
cannot easily distinguish between a large number of similar tones, and
hence, if we want to make different continuous levels distinguishable,
we need to use fewer colors. If you want a true continuous scale, you
can always feed a color brewer palette into scale_color_gradientn,
for instance.
15.5.2 Statistical Transformations
If you look at the above bar chart, you’ll notice that the the y axis was defined for you as the count of elements that have the particular type. This count isn’t part of the data set (it’s not a column in mpg), but is instead a statistical transformation that the geom_bar automatically applies to the data. In particular, it applies the stat_count transformation, simply summing the number of rows each class appeared in the dataset.
ggplot2 supports many different statistical transformations. For example, the “identity” transformation will leave the data “as is”. You can specify which statistical transformation a geom uses by passing it as the stat argument:
# bar chart of make and model vs. mileage
# quickly (lazily) filter the dataset to a sample of the cars: one of each make/model
new_cars <- mpg %>%
mutate(car = paste(manufacturer, model)) %>% # combine make + model
distinct(car, .keep_all = TRUE) %>% # select one of each cars -- lazy filtering!
slice(1:20) # only keep 20 cars
# create the plot (you need the `y` mapping since it is not implied by the stat transform of geom_bar)
ggplot(new_cars) +
geom_bar(mapping = aes(x = car, y = hwy), stat = "identity") +
coord_flip() # horizontal bar chart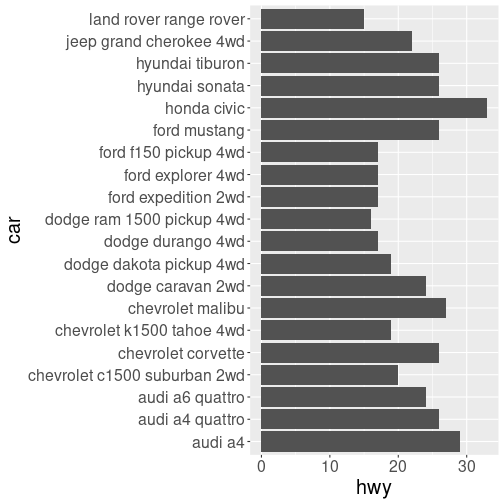
plot of chunk bar_chart
Additionally, ggplot2 contains stat_ functions (e.g., stat_identity for the “identity” transformation) that can be used to specify a layer in the same way a geom does:
# generate a "binned" (grouped) display of highway mileage
ggplot(data = mpg) +
stat_bin(aes(x = hwy, color = hwy), binwidth = 4) # binned into groups of 4 units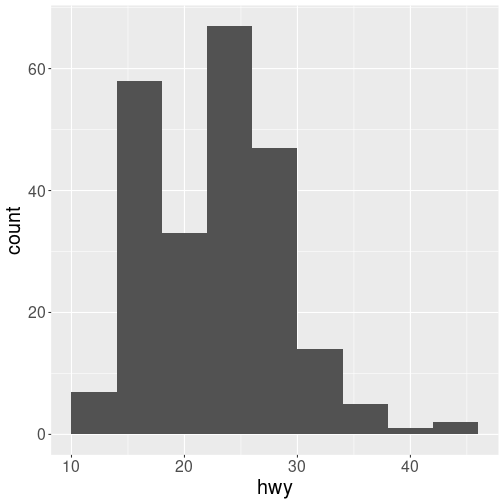
plot of chunk stat_summary
Notice the above chart is actually a histogram! Indeed, almost every stat transformation corresponds to a particular geom (and vice versa) by default. Thus they can often be used interchangeably, depending on how you want to emphasize your layer creation when writing the code.
15.5.3 Position Adjustments
In addition to a default statistical transformation, each geom also
has a default position adjustment which specifies a set of “rules”
as to how different components should be positioned relative to each
other.
One of the plot type where the position adjustment is used quite often
is geom_col() and geom_histogram().
This allows you to show different sides of the same
data. Below we demonstrate four different histograms of diamond size
depending on cut. Each of these histograms stresses a different side
of data.
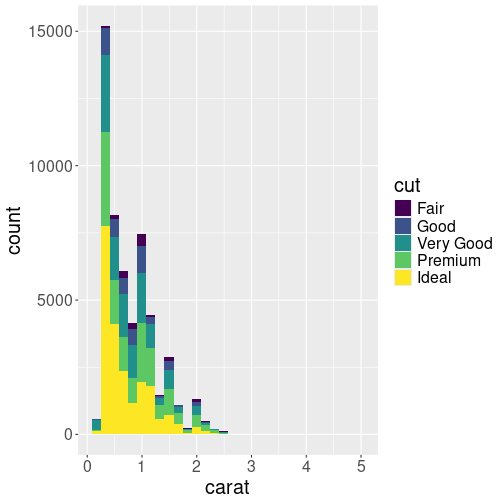
When we color fill the diamond histogram by cut, then by default the bars are stacked on top of each other:
Let’s show this by plotting the histogram of diamonds’ mass (carat), by coloring the bars different according to cut:
This shows the histogram–count by binned carat values. The counts are done separately for different cut-s, and the corresponding bars are stacked on top of each other. This plot is good to show the overall distribution of diamonds, and show what kind of role do gems of different cut play there. We see that by far the most diamonds are small, less than 0.5 ct. But there are secondary peaks at 1ct, 1.5ct and 2ct. We can also see that there are many “ideal” diamonds, although the number differ in different bins.
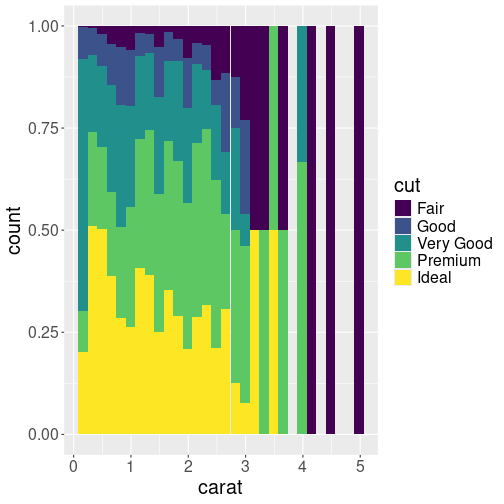
Another histogram of carat, split into five different groups by cut. Now all the bars are of the same height, stressing the proportion of different cuts.
But the previous plot is not very informative if we are interested in
comparing the share of different cuts. The bars are of different
lenbth, and in particular the shorter ones, it is hard to see what
proportion of ideal and other diamonds are there. But we can make the
proportion visible by making the bars of equal height with pos = "fill" argument:
In this form, the histogram shows that ideal cut is more common for small diamonds, and larger diamonds tend to be of less valuable cut.
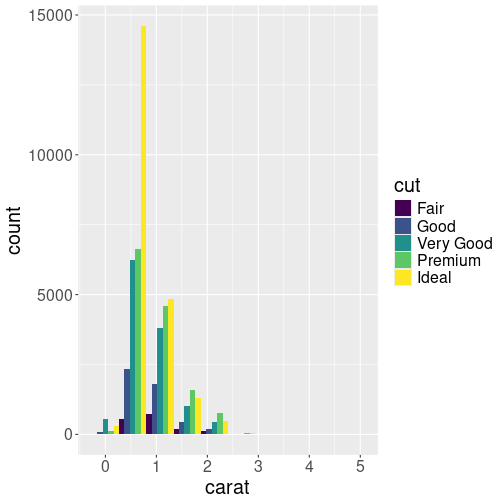
Third similar histogram. Now the bars are located next to each other, allowing a comparison of the mass distribution for differently cut diamonds. We only show 10 bins to make the bars easier to read.
But if we want to compare how the differently cut diamonds are
distributed, neither of the plots above are good. We may want to put
the bars next to each other with position = "dodge" instead:
(We only show 10 bins to make the bars easier to read.) This plot
gives a somewhat similar messages as the one above (position = "fill"). This time, however, we can also see that diamonds between
0.5 to 2.5ct are the most common ones of every cut,
diamonds larger than 3ct are
extremely rare, no matter which cut you are looking at.
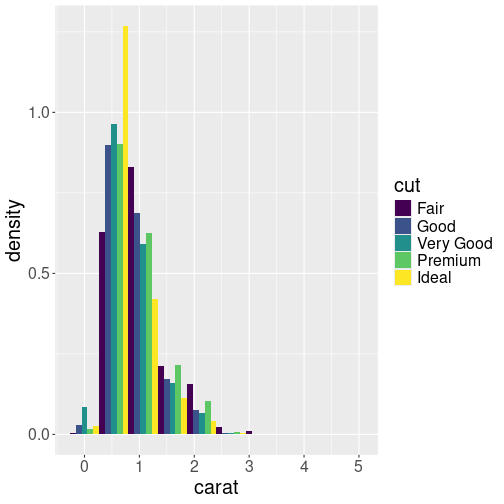
Plotting density instead of counts. This is a better way to see what kind of diamonds are more or less common for a given cut.
Finally, if we are not interested in the distribution of different
cuts given the diamond size, we can compare the densities by setting
y = ..density.. (see Sectino 15.3.4)
in the aesthetics mapping:
Here we can see that most common ideal-cut diamonds are around 0.5ct, but the most common fair-cut diamonds are of 1ct.
As you can see from these examples, there is a variety of ways to display the same data. Each of these sends a different message, and which one you want to use, depends on which side you want to stress.
15.5.4 Styling with Scales
Whenever you specify an aesthetic mapping, ggplot maps the
corresponding data variables values to those aesthetic properties.
But how exactly this mapping happens, is determined through scales.
We discussed color scales in Section 15.5.1
above, now we discuss the other scales.
15.5.4.1 Size, type, linestyle, and alpha
Besides color, there is a number of related attributes:
- size determines either the point size, the line width, or width of the outline of area objects, such as bars.
- alpha determines the transparency of objects with “1” being completely oblique, and “0” being completely transparent (invisible).
- shape selects from different point shapes.
- linestyle selects from different line styles, such as solid, dotted or dashed.
Out of these, size and alpha can have any value and hence they can display continuous values. However, point shapes and line styles can only display a limited set of discrete values and give an error if fed with continuous data.
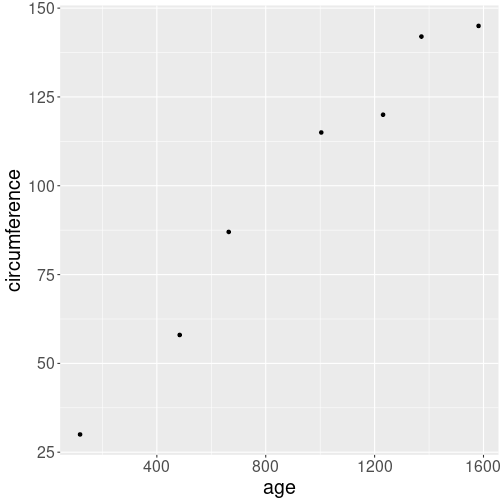
Below, we demonstrate the usage of linestyle and point shape scales with orange tree data (see Section 11.2):
## # A tibble: 2 × 3
## Tree age circumference
## <dbl> <dbl> <dbl>
## 1 4 1582 214
## 2 3 118 30This dataset shows growth of the circumference of five different orange trees through almost 5 years.
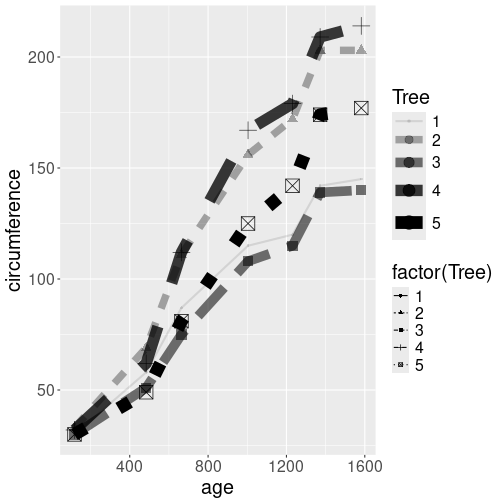
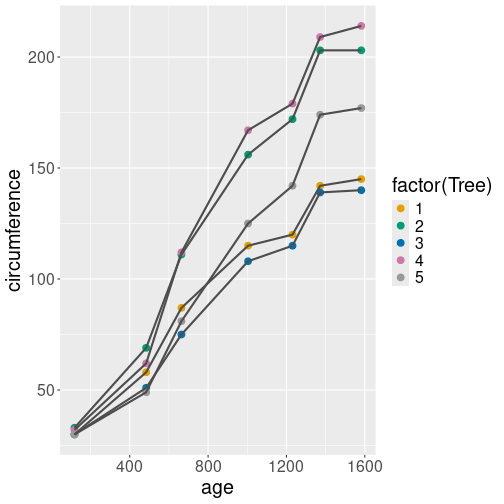
Growth of orange trees. Point size and shape, line width and style, and transparency, all differ by the tree.
We start by transforming the continuous variable Tree into a
discrete discrete with mutate(tree = factor(Tree)). This is because
we cannot map continuous values to a discrete scale (point shape and
line style), see Section 15.5.1.1.
Thereafter we make the plot, and map the tree number to
all four above-mentioned aesthetics:
orange %>%
mutate(tree = factor(Tree)) %>%
ggplot(aes(age, circumference,
shape = tree,
linetype = tree,
alpha = tree,
size = tree)) +
geom_line() +
geom_point()The plot, using the default scales, is not very good. All the trees are marked with black color, but as the black lines are at least somewhat transparent, they appear as different shades of gray. Also, the line styles are hard to comprehend, notably a very wide dashed line resembles a series of dots instead. Finally, we also get warnings advising us not to use continuous scales (alpha and size) for discrete values–we transformed “tree” to be a categorical variable.
aes(shape = factor(Tree), size = Tree).
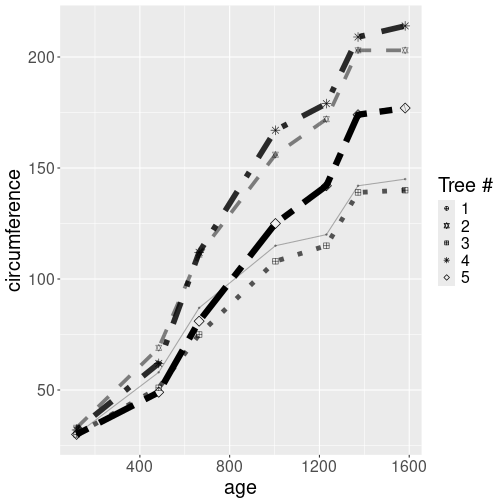
The same plot as above, just this time using manually designed scales.
orange %>%
ggplot(aes(age, circumference,
shape = factor(Tree),
linetype = factor(Tree),
alpha = Tree,
size = Tree)) +
geom_line() +
geom_point() +
scale_shape_manual(
values = c("1" = 10, "2" = 11,
"3" = 12, "4" = 8,
"5" = 5)) +
scale_linetype_manual(
values = c("1" = "solid", "2" = "dashed",
"3" = "dotted", "4" = "dotdash",
"5" = "twodash")) +
scale_size_continuous(range=c(0.5,3)) +
scale_alpha_continuous(range=c(0.3,1)) +
guides(linetype = "none",
size = "none",
alpha = "none") +
labs(shape = "Tree #")First, we hand-pick the values for two discrete scales. Each tree
will have it’s own dedicated line type and point shape.
For the continuous scales, we do not pick the individual values but
adjust the ranges instead. For line widths we choose values
between
0.5 and 3 (range = c(0.5, 3)) to make the lines of more equal width, and for alpha we
do a similar conversion forcing the lines to
be a bit more oblique. Finally, we tell that we do not want to see
the linetype, size, and alpha legends on the figure; and adjust the
legend label.
15.5.4.2 x and y
# mileage relationship, ordered in reverse
ggplot(data = mpg) +
geom_point(mapping = aes(x = cty, y = hwy)) +
scale_x_reverse()Similarly, you can use scale_x_log10() to plot on a logarithmic scale.
You can also use scales to specify the range of values on a axis by passing in a limits argument. This is useful for making sure that multiple graphs share scales or formats.
# subset data by class
suv <- mpg %>% filter(class == "suv") # suvs
compact <- mpg %>% filter(class == "compact") # compact cars
# scales
x_scale <- scale_x_continuous(limits = range(mpg$displ))
y_scale <- scale_y_continuous(limits = range(mpg$hwy))
col_scale <- scale_colour_discrete(limits = unique(mpg$drv))
ggplot(data = suv) +
geom_point(mapping = aes(x = displ, y = hwy, color = drv)) +
x_scale + y_scale + col_scale
ggplot(data = compact) +
geom_point(mapping = aes(x = displ, y = hwy, color = drv)) +
x_scale + y_scale + col_scale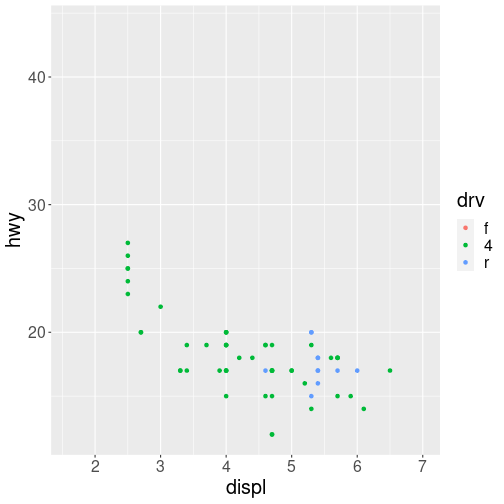
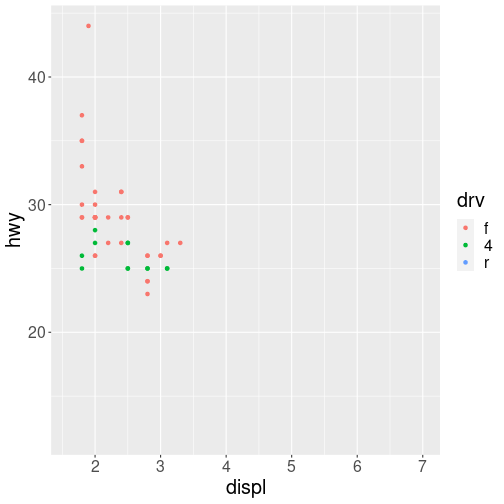
Notice how it is easy to compare the two data sets to each other because the axes and colors match!
These scales can also be used to specify the “tick” marks and labels; see the resources at the end of the chapter for details. And for further ways specifying where the data appears on the graph, see the Coordinate Systems section below.
15.5.5 Coordinate Systems
The next term from the Grammar of Graphics that can be specified is the coordinate system. As with scales, coordinate systems are specified with functions (that all start with coord_) and are added to a ggplot. There are a number of different possible coordinate systems to use, including:
coord_cartesianthe default cartesian coordinate system, where you specifyxandyvalues.coord_flipa cartesian system with thexandyflippedcoord_fixeda cartesian system with a “fixed” aspect ratio (e.g., 1.78 for a “widescreen” plot)coord_polara plot using polar coordinatescoord_quickmapa coordinate system that approximates a good aspect ratio for maps. See the documentation for more details.
Most of these system support the xlim and ylim arguments, which specify the limits for the coordinate system.
15.5.6 Facets
Facets are ways of grouping a data plot into multiple different pieces (subplots). This allows you to view a separate plot for each value in a categorical variable. Conceptually, breaking a plot up into facets is similar to using the group_by() verb in dplyr, with each facet acting like a level in an R factor.
You can construct a plot with multiple facets by using the facet_wrap() function. This will produce a “row” of subplots, one for each categorical variable (the number of rows can be specified with an additional argument):
# a plot with facets based on vehicle type.
# similar to what we did with `suv` and `compact`!
ggplot(data = mpg) +
geom_point(mapping = aes(x = displ, y = hwy)) +
facet_wrap(~class)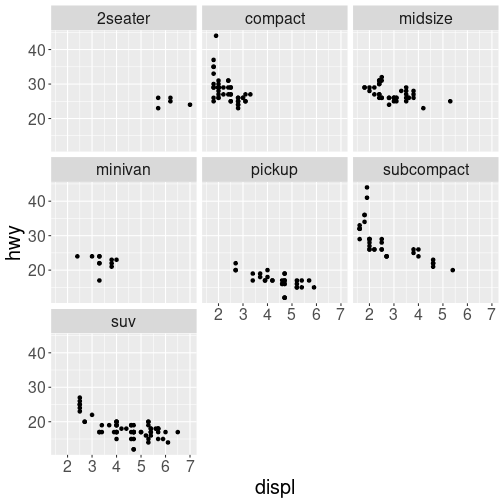
plot of chunk facets
Note that the argument to facet_wrap() function is written with a tilde (~) in front of it. This specifies that the column name should be treated as a formula. A formula is a bit like an “equation” in mathematics; it’s like a string representing what set of operations you want to perform (putting the column name in a string also works in this simple case). Formulas are in fact the same structure used with standard evaluation in dplyr; putting a ~ in front of an expression (such as ~ desc(colname)) allows SE to work.
- In short: put a
~in front of the column name you want to “group” by.
15.5.7 Labels & Annotations
Textual labels and annotations (on the plot, axes, geometry, and legend) are an important part of making a plot understandable and communicating information. Although not an explicit part of the Grammar of Graphics (they would be considered a form of geometry), ggplot makes it easy to add such annotations.
You can add titles and axis labels to a chart using the labs() function (not labels, which is a different R function!):
ggplot(data = mpg) +
geom_point(mapping = aes(x = displ, y = hwy, color = class)) +
labs(
title = "Fuel Efficiency by Engine Power, 1999-2008", # plot title
x = "Engine power (litres displacement)", # x-axis label (with units!)
y = "Fuel Efficiency (miles per gallon)", # y-axis label (with units!)
color = "Car Type"
) # legend label for the "color" property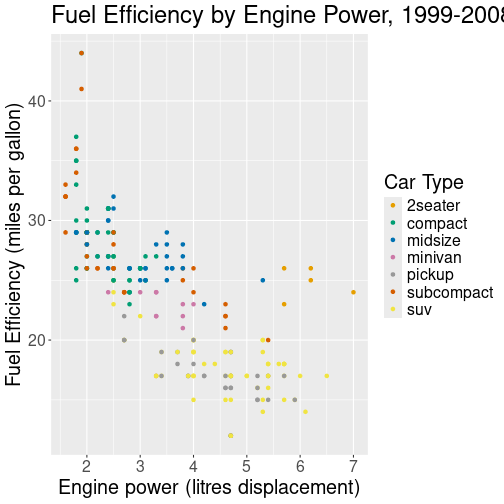
plot of chunk labels
It is possible to add labels into the plot itself (e.g., to label each point or line) by adding a new geom_text or geom_label to the plot; effectively, you’re plotting an extra set of data which happen to be the variable names:
# a data table of each car that has best efficiency of its type
best_in_class <- mpg %>%
group_by(class) %>%
filter(row_number(desc(hwy)) == 1)
ggplot(data = mpg, mapping = aes(x = displ, y = hwy)) + # same mapping for all geoms
geom_point(mapping = aes(color = class)) +
geom_label(data = best_in_class, mapping = aes(label = model), alpha = 0.5)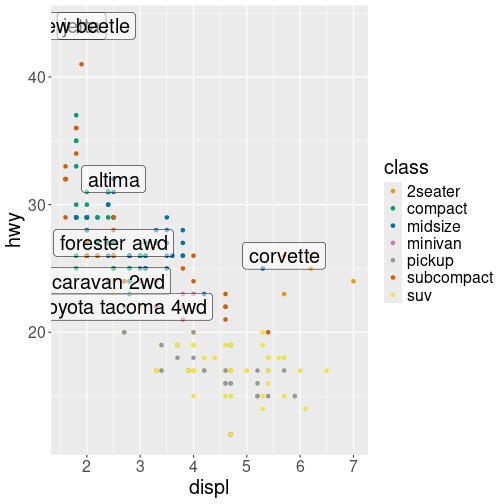
plot of chunk annotations
R for Data Science (linked in the resources below) recommends using the ggrepel package to help position labels.
15.6 Creating Maps
ggplot’s functionality can be easily applied to create maps. Maps are largely polygons filled with certain colors (e.g. administrative units or lakes), and amended with various line segments (e.g. rivers), dots (e.g. cities) and text. ggplot possesses all these tools.
15.6.1 How maps are made: a hand carved example
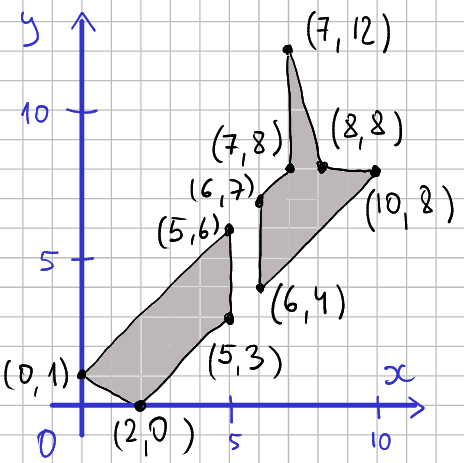
The map is made of lines that connect vertices. We have put the lines on a 2-D plane and marked the coordinate pairs for each vertex, e.g. in the lower-left corner there is a line that connects point (0,1) to (2,0). The two islands (South Island and North Island) are filled with gray.
If we want to plot this data as a map we should just draw the black lines that connect the vertices. There are a few details we have to ensure we get right:
- We must be careful to only connect the
lines that correspond to the coastline of each island, we should not
draw a line across the sea from one coastline to the other.
- We must connect the points in the correct order, not in a criss-cross manner.
- And finally, we have to ensure that the polygons are closed, i.e. the last vertex is connected to the first one.
Next, let’s create this map. We start with creating a data frame of the vertices. This is a little tedious process as data frames expect x and y to be given separately while for us it is easier to thing of those as pairs. So you may consider doing such data entry in a spreadsheet instead.
nz <- data.frame(x = c(0, 2, 5, 5, # south island
6, 10, 8, 7, 7, 6), # north island
y = c(1, 0, 3, 6, # south island
4, 8, 8, 12, 8, 7)) # north islandTo demonstrate the polygon plotting, let’s make a plot of the map vertices we entered:
plot of chunk unnamed-chunk-34
We ask the outline to be drawn in black, and the polygons not to be
filled (fill = NA).
The result has a number of problems, in particular it connects both
the islands. This is not surprising as we did not tell ggplot in
any way which points form separate islands. Note that geom_polygon
connects the last and first vertex automatically, and as we entered
the vertices in a correct order, we got a nice coastline plot.
As the next step,
let’s add a group id, and id for each separate polygon. This is
typically called group and consists of a numeric id. However, we
can give it also a more descriptive id, e.g. “south” and “north” for
south and north island respectively. Thereafter we tell ggplot that
each group is a separate polygon by using group aesthetic:
nz$group <- c("south", "south", "south", "south",
"north", "north", "north", "north", "north", "north")
ggplot(nz, aes(x, y, group=group)) +
geom_polygon(col="black", fill=NA)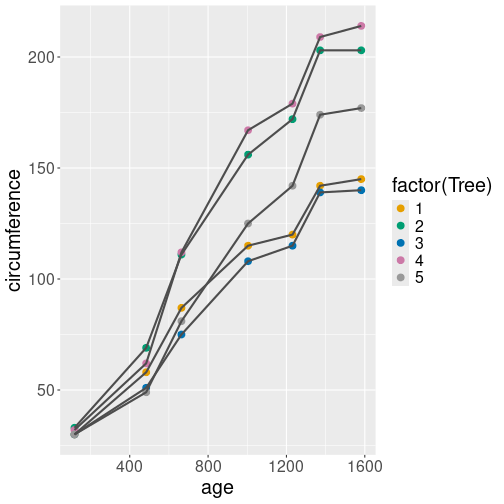
plot of chunk unnamed-chunk-35
Indeed, we got the two islands separated.
Finally, in order to avoid distorted coordinates, we use
coord_quickmap to ensure that the lengths correspond to the real map
lengths. We also fill the islands green:
nz$group <- c("south", "south", "south", "south",
"north", "north", "north", "north", "north", "north")
ggplot(nz, aes(x, y, group=group)) +
geom_polygon(col="black", fill="seagreen3") +
coord_quickmap()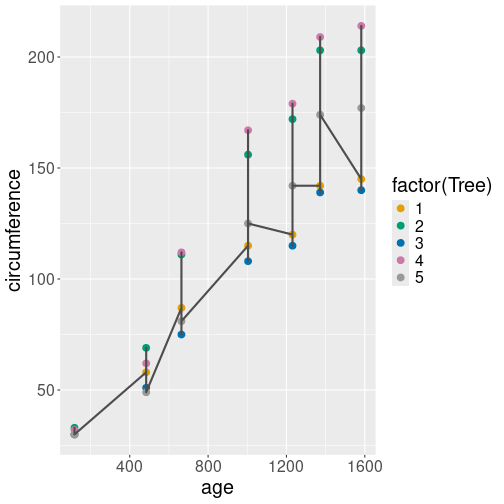
plot of chunk unnamed-chunk-36
The result is fairly similar to real maps, except that our manually designed coastline is far too simplistic. But now we have all the tools we need to plot real maps given we get the suitable data.
15.6.2 Bonus maps: map_data()
Fortunately we do not have to create maps manually. ggplot includes a few common maps, and there are straightforward tools to load standard map data, such as what you can dowload from the websites.
ggplot can directly access maps in the package maps using function
map_data(). First you need to install that package, or you’ll see
an error message
Error in
map_data(): ! The package “maps” is required formap_data()
(See Section 6.5 for how to install packages.) For instance, the world map can be accessed with
## long lat group order region subregion
## 1 -69.89912 12.45200 1 1 Aruba <NA>
## 2 -69.89571 12.42300 1 2 Aruba <NA>
## 3 -69.94219 12.43853 1 3 Aruba <NA>
## 4 -70.00415 12.50049 1 4 Aruba <NA>
## 5 -70.06612 12.54697 1 5 Aruba <NA>
## 6 -70.05088 12.59707 1 6 Aruba <NA>This dataset is very similar to what we constructed for New Zealand above. The variables long and lat denote longitude and latitude (we used x and y above), and group is of the same name. There are a few differences though. Most importantly, order denotes the order by which the points must be connected. In case of the NZ map above, we created the vertices in the correct order. The same is true here–the vertices are in correct order, but the order may be violated after certain operations. If this is the case, then we can use the order variable to restore the order (but remember to group by group—the order is valid within each group!). Besides the order, we have region–the country name, and subregion that contains the name of e.g. the corresponding U.S. states (Aruba does not have any subregions).
We can plot the map as
ggplot(world, aes(long, lat, group=group)) +
geom_polygon(fill="seagreen", col="black", size=0.3) +
coord_quickmap()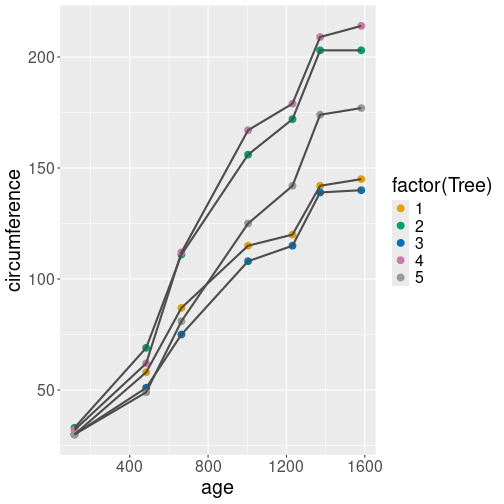
A quick world map with ggplot.
This map contains the continents and country boundaries. But it is more interesting if we, instead, color the countries based on some kind of data. Let’s demonstrate this using concept similarity data. This is a dataset that computes the similarity between country names and a set of different words, and it is calculated based on texts that were scraped from internet around 2015. The dataset looks like
## # A tibble: 2 × 12
## country terrorism nuclear trade battery regime volcano palm fir
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 aruba 0.0891 -0.011 0.0504 -0.01 -0.0356 0.166 0.293 0.0965
## 2 afghanistan 0.447 0.220 0.109 0.0578 0.180 0.129 0.116 0.129
## flood drought mountain
## <dbl> <dbl> <dbl>
## 1 0.0158 0.0581 0.107
## 2 0.159 0.160 0.161One can see that “Afghanistan” and “terrorism” are much more similar (similarity 0.447) than e.g. “Afghanistan” and “trade” (similarity 0.109). We do not go into details here about how the similarity is measured, but broadly, it means how frequently are these words used in a similar context.
Before we can plot the similarity data on a map, we have to merge to map data with similarity data. But note that that the map data is much larger (99338 rows) than similarity data (252 rows). This is because the map data contains one data point for each turn of the coastline and boundary, while the similarity data only contains a single value for each country. Hence we want to merge the map data in a way that we keep all world data points, and assign the same similarity value for each map datapoint that describes the same country. Also note that the merge key–the information that connects the map and similarities–is the country name. We also need to ensure that the country names have the same case, here we need to convert the world map country names to lower case. We can achieve this with (See section 11.7 for more about merging data):
similarityMap <- world %>%
mutate(country = tolower(region)) %>%
merge(similarity, by = "country", all.x = TRUE) %>%
group_by(group) %>% # re-order as merge may change the order
arrange(order)
similarityMap %>%
head(2)## # A tibble: 2 × 18
## # Groups: group [1]
## country long lat group order region subregion terrorism nuclear trade
## <chr> <dbl> <dbl> <dbl> <int> <chr> <chr> <dbl> <dbl> <dbl>
## 1 aruba -69.9 12.5 1 1 Aruba <NA> 0.0891 -0.011 0.0504
## 2 aruba -69.9 12.4 1 2 Aruba <NA> 0.0891 -0.011 0.0504
## battery regime volcano palm fir flood drought mountain
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 -0.01 -0.0356 0.166 0.293 0.0965 0.0158 0.0581 0.107
## 2 -0.01 -0.0356 0.166 0.293 0.0965 0.0158 0.0581 0.107The result is just what it is supposed to be–a combination of the map data and word similarity data. Note that we re-ordered the vertices by group as the order may change when merging.
Finally, we can make a plot as we did above, but this time filling the polygons by a given word, e.g. by "trade:
ggplot(similarityMap, aes(long, lat, group=group, fill=trade)) +
geom_polygon(col="black", size=0.3) +
coord_quickmap()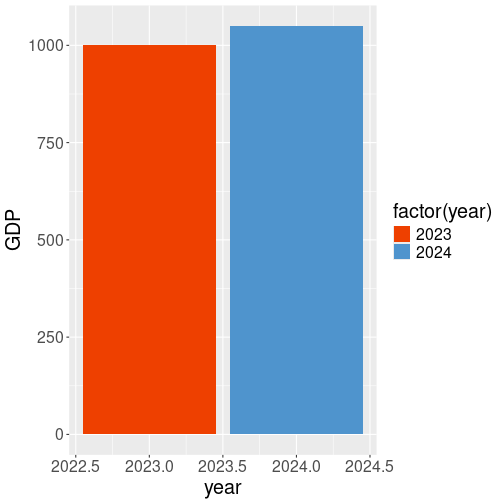
A world map where countries are colored according data, here according to how similar are the corresponding country names to the word “trade”.
We can see that the country name “China” is most often used in a similar context as “trade”, while the countries in central Asia and in Africa are not.
Exercise 15.3 Merge data but leave out re-ordering. What happens?
Exercise 15.4 Make similar plots but this time use words “fir” and “palm”. Do you see how geographic location is associated with trees?
15.7 Programming with ggplot2
ggplot is well suited to be incorporated into code. So far, we have been focusing on the interactive usage, or usage in small code snippets. When you run the code in a more extensive program, there are a number of issues you may run into. Here we discuss some of these.
15.7.1 Outputting plots
The typical usage of ggplot in short code snippets is something like
When you run this code, you’ll see the plot popping up in the plot
window. This may make you to think that the ggplot() function that
itself draws the image on screen. But this is not true!
A call to ggplot() just creates a ggplot-object, a data structure
that contains data and all other necessary details for creating the
plot. But it does not create the image.
The image is created instead by the print-method. This is analogous
with all other R expression on the console–if you just type an
expression, then R evaluates and prints the result.
This is why we can use it as a manual calculator for simple math, such as 2 + 2. The same is true for ggplot: it returns a ggplot-object, and given you don’t store it into a variable, it is printed, and the print method of ggplot-object actually makes the image. This is why we can immediately see the images when we work with ggplot on console.
Things may be different, however, if we do this in a script. When you execute a script, the returned objects are not printed, even if you do not save those in a variable. For instance, the script
will not produce any output when sourced as a single script (Source-d, not sourced with echo, and not run line-by-line). If this is the problem you run into, then you may want to store the plot into a variable and afterward print it explicitly:
As an additional bonus, now you have stored your plot in a variable and you can also add additional layers to it (see Section 15.7.2).
Note that this also applies to other contexts where ggplot is used, e.g. when making plots in shiny (see Section 18).
In scripts we often want the code not to produce image on screen, but store it in a file instead. This can be achieved in a variety of ways, for instance through redirecting graphical output to a pdf device with the command pdf():
data <- diamonds %>%
sample_n(1000)
p <- ggplot(data) +
geom_point(aes(carat, price)) # store here
pdf(file="diamonds.pdf", width=10, height=8)
# redirect to a pdf file
print(p) # print here
dev.off() # remember to close the fileAfter redirecting the output, all plots will be written to the pdf file (as separate pages if you create more than one plot). Note you have to close the file with dev.off(), otherwise it will be broken. There are other output options besides pdf, you may want to check jpeg and png image outputs. Finally, ggplot also has a dedicated way to save individual plots to file using ggsave.
15.7.2 Re-using your code: adding layers with +
You frequently need to make multiple rather similar plot. You want the plots to be rather similar but not exactly the same. This means most of the plotting commands are the same, but a few are different. A good way to achieve this in ggplot is to store the parts of your plot you want to re-use into variables. For instance, let’s do two plots of diamonds, one in linear-linear, and the other in log-log scale.
Two similar plots, done by re-using the same code.
First, we select a subsample of diamonds and make a simple scatterplot:
This scatterplot is saved as p, and we can create the plot by just printing it as
As we did not specify any special scale, the plot will be in linear-linear scale. The other plot is created from the same variable p by adding the log-log scales:
As we do not store this into a new variable, the result will just be printed (plotted).
Note how we just add more layers to p, in a similar fashion as one
can add numbers to a numberic variable. The + sign understands that
these are ggplot objects and combines the appropriate layers instead.
15.7.3 Indirect variable names
Another common task when programming is to use indirect variable names (see Section 10.3.1).
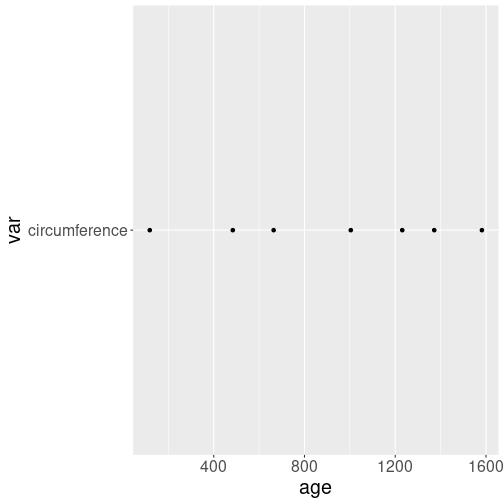
Indirect variable name used in a wrong way. ggplot assumes that the vertical position is given through the workspace variable “var”, and it’s value is “circumference”. That’s why every signle dot is at level “circumference”.
It is not immediately obvious how to do it–a naive attempt with
data <- Orange %>%
filter(Tree == 1)
var <- "circumference"
ggplot(data, aes(age, var)) +
geom_point()will result in a weird plot that is almost certainly not what you want.
an error where ggplot complains about “var” not found. The problem is similar as with dollar versus double bracket notation in case of data frames–ggplot expects “var” to be the data variable name, and complains that it cannot find it.
Indirect variable names can be used with aes_string(). Note that
“age” must be quoted too.
Fortunately, there is an easy remedy. aes_string(), instead of
aes() will expect the arguments to be strings, not unqoted variable
names. And one can easily pass string values indirectly:
data <- Orange %>%
filter(Tree == 1)
var <- "circumference"
ggplot(data, aes_string("age", var)) +
geom_point()Note that all variable names must be passed as character to
aes_string(), so you must write aes_string("age", var), not
aes_string(age, var). “Var” must be left unquoted as it is a
workspace variable, but “age” is the name of a data variable.
15.8 More geoms and plot types
Let’s do this using ice extent data. The dataset originates from NSIDC (National Snow & Ice Data Center) and looks like
## year month data.type region extent area time
## 1059 2022 12 NRTSI-G N 11.92 10.23 2022.958
## 1060 2022 12 NRTSI-G S 8.69 5.12 2022.958
## 1061 2023 1 NRTSI-G N 13.35 11.83 2023.042
## 1062 2023 1 NRTSI-G S 3.23 1.95 2023.042The relevant variables here are
- time: fractional year in the mid-month (\(\mathit{time} = \mathit{year} + \mathit{month}/12 - 1/24\)).
- extent: sea ice extent, M \(km^2\). Sea ice extent is sea area where ice concentration is over 15%. This is a measure of sea ice that is less error prone that sea ice area, area where sea is completely frozen over.
- region: “N”/“S” for Northern or Southern hemisphere.
Section 15.3 introduced geoms, and demonstrated how to use those to create line plots and scatterplots. Here we discuss a selection of other plot types, and other tasks that can be achieved with different geoms. Here we discuss other plot types and additional elements one can add to the plots using different geoms.
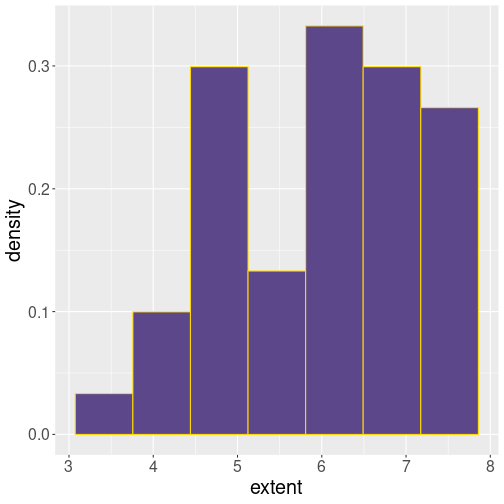
Histogram of September ice extent for the sample period.
The histogram of the corresponding data looks like (see Section 15.3.4 for more about the histograms):
ggplot(septemberData,
aes(extent)) +
geom_histogram(
aes(y = ..density..),
bins=10,
fill="deepskyblue", col="black"
)We see that the smallest extent values are less than 3 (M km\(^2\)), and the largest values are close to 8.
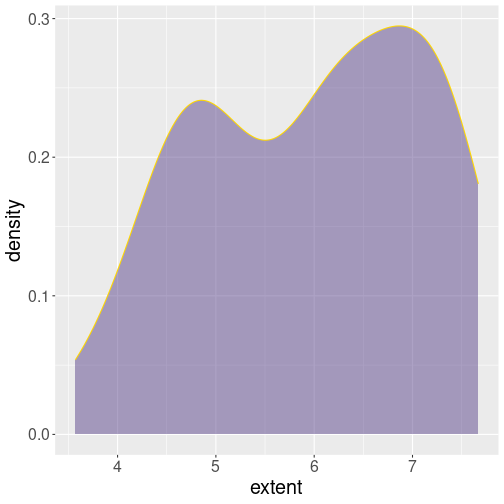
Smooth density curve (black), filled from below with semi-transparent blue.
Unfortunately, histograms may be sensitive to the number and location
of bins, and hence it may be useful to show data in a “smoothed
histogram” version. This can be done with geom_density():
Alone, geom_density() just draws the smooth black curve, when
specifying fill =, it fills the area under the curve. Here we also
set alpha = 0.5, making the fill color semi-transparent to make the
underlying coordinate lines somewhat visible.
There are also a number of geoms which’ primary purpose is not to
display data but to mark certain values on the figure. This includes
geom_vline() for vertical lines, geom_hline() for horizontal
lines, and geom_abline() for diagonal lines. These geoms can be
used to display data, but the result is often not particularly useful.
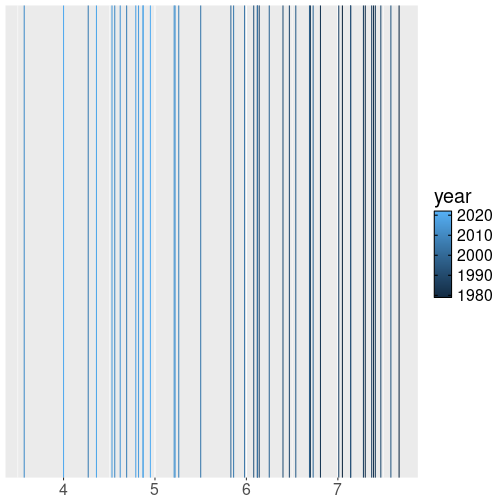
All September ice extents, displayed as vertical lines.
For instance, we can plot all the ice extent using vertical lines while coloring those according to year:
ggplot(septemberData) +
geom_vline(
## have to specify 'xintercept' here,
## not in ggplot()!
aes(xintercept = extent, col=year)
) +
viridis::scale_color_viridis()The figure is somewhat useful (it is a form of rugplot), but alone, it is usually not the best way to visualize data. Nevertheless, when colored like this, it indicates that the largest September ice extent in data occured in 1980-s, 2010-s tend to be at the low end.
ggplot(septemberData, aes(extent)) +
geom_density() +
geom_vline(
xintercept=c(
mean(septemberData$extent),
median(septemberData$extent)
),
col = c("orangered1", # mean is red
"seagreen4") # median is green
)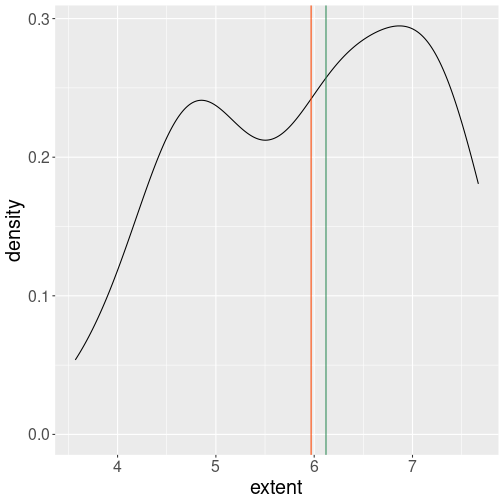
The period average and median ice extent marked as vertical lines of different color.
Instead, the lines are typically used to display certain values on the figure. For instance, we can add the sample mean and median to the density plot as vertical lines of different color:
ggplot(septemberData, aes(extent)) +
geom_density() +
geom_vline(
xintercept=c(
mean(septemberData$extent),
median(septemberData$extent)
),
col = c("orangered1", # mean is red
"seagreen4") # median is green
)Note that while aes() accepts the data variables names directly, the
xintercept = inside geom_vline() does look for workspace variables
only. One has to use dollar notation or something similar to extract
data variables from the data frame.
15.9 Other Visualization Libraries
ggplot2 is easily the most popular library for producing data visualizations in R. That said, ggplot2 is used to produce static visualizations: unchanging “pictures” of plots. Static plots are great for for explanatory visualizations: visualizations that are used to communicate some information—or more commonly, an argument about that information. All of the above visualizations have been ways to explain and demonstrate an argument about the data (e.g., the relationship between car engines and fuel efficiency).
Data visualizations can also be highly effective for exploratory analysis, in which the visualization is used as a way to ask and answer questions about the data (rather than to convey an answer or argument). While it is perfectly feasible to do such exploration on a static visualization, many explorations can be better served with interactive visualizations in which the user can select and change the view and presentation of that data in order to understand it.
While ggplot2 does not directly support interactive visualizations, there are a number of additional R libraries that provide this functionality, including:
ggvisis a library that uses the Grammar of Graphics (similar toggplot), but for interactive visualizations. The interactivity is provided through theshinylibrary, which is introduced in a later chapter.Bokeh is an open-source library for developing interactive visualizations. It automatically provides a number of “standard” interactions (pop-up labels, drag to pan, select to zoom, etc) automatically. It is similar to
ggplot2, in that you create a figure and then and then add layers representing different geometries (points, lines etc). It has detailed and readable documentation, and is also available to other programming languages (such as Python).Plotly is another library similar to Bokeh, in that it automatically provided standard interactions. It is also possible to take a
ggplot2plot and wrap it in Plotly in order to make it interactive. Plotly has many examples to learn from, though a less effective set of documentation than other libraries.rChartsprovides a way to utilize a number of JavaScript interactive visualization libraries. JavaScript is the programming language used to create interactive websites (HTML files), and so is highly specialized for creating interactive experiences.
There are many other libraries as well; searching around for a specific feature you need may lead you to a useful tool!
Resources
- gglot2 Documentation (particularly the function reference)
- ggplot2 Cheat Sheet (see also here)
- Data Visualization (R4DS) - tutorial using
ggplot2 - Graphics for Communication (R4DS) - “part 2” of tutorial using
ggplot - Graphics with ggplot2 - explanation of
qplot() - Telling stories with the grammar of graphics
- A Layered Grammar of Graphics (Wickham)
RColorBrewer::display.brewer.all() calls the function display.brewer.all() from the RColorBrewer package, without loading it first. It is mostly equivalent to two separate commands,
library(RColorBrewer)anddisplay.brewer.all().↩