Chapter 6 Preliminary data analysis
This section describes the first steps we usually take when starting working with a new dataset. The main message here is: understand your data.
6.1 Different variable types
We discussed the different kind of data in Section 3.2. That discussion was focused on data and how we understand it. Now we continue this discussion looking at computers and how computers represent it. Obviously, computer representation reflects of our understanding, but the details differ. For working with data on computers, it is important to understand the “computer’s mind”.
6.1.3 Categorical variables
Quite an important category are categorical variables, variables that represent values that are not numbers. In computer memory, these can be represented both as text, or as numbers.
If the numbers are represented as text, then all is well–R understands that text is not numbers, hence it is categorical. But when the categories are numbers, you may run into a trouble. The problem here is that R has no way of knowing if numbers are numbers (i.e. they can be added and averaged), or if they are categories (that cannot be added or averaged). For instance, in Titanic data (see Section B.7), the passenger class is coded as “1”, “2” or “3”. These are not numbers! These are categories. You cannot do mathematics like “first class + second class = third class”. This does not make any sense! However, they are stored in memory as numbers, and hence R, by default, treats these as any other numbers, and is happy to make all sorts of computations with these.
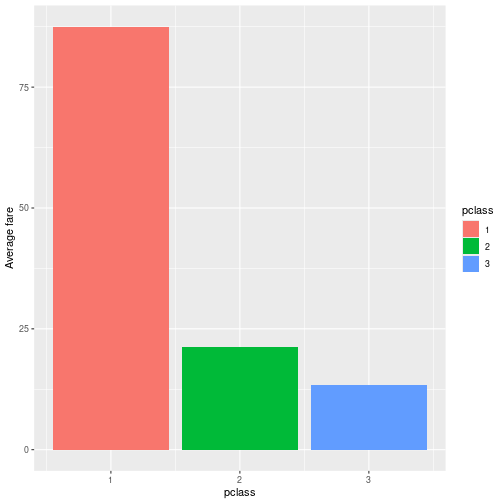
This causes problems when using certain functionality, e.g. plotting, where data handling depends on the data type. For instance, in case of categorical variables, we may want to color the different classes in clear distinct colors. The image here display the average fare on Titanic by passenger class. The classes are clearly distinct, depicted with very different colors.
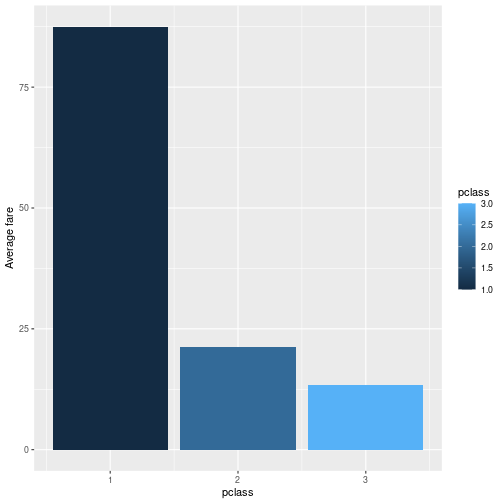
However, when R thinks that pclass is a number, it may display the colors on the same continuous scale instead. You can also see that the color key has middle values, such as 2.5 and 1.5. This is usually not what we want.
In such cases, one should convert the numbers to categoricals using
the factor() function. So instead of plotting average fare versus
pclass, you should plot average fare versus factor(pclass). See
more in Section 10.2.5.
6.2 Preliminary data analysis
While the preliminary analysis may feel a bit boring and too simplistic, it is an extremely important step. You should do it every time when you encounter a new dataset. There are good reasons to analyze it even if the dataset is well documented and originates from a very credible source. For instance, did you download the correct file? Did you open it correctly? Also, there are plenty of examples where high-quality documentation does not quite correspond to the actual dataset. At the end, we need to know what is in data, we are not much concerned about what is in the documentation.
This section primarily concerns about the aspects of data quality and variable coding, the preliminary statistical analysis is discussed in Section 7.2.
Through this section we use Titanic data, see Section B.7. We load it as
For beginners, it may be advantageous to use RStudio’s graphical data viewer (See Section 3.7) in order to get the very basic idea about the dataset. But here we discuss how to achieve the same functionality using commands. This is in part because the viewer only offers a limited functionality, but also because in that way we can learn the much more flexible command approach.
6.2.1 Is this a reasonable dataset?
The first step, before we begin any serious analysis, is to take a look to see what the dataset actually contains.
A good first step is to just look at what is there in data. The first few lines of a dataset can be printed as
## # A tibble: 6 × 14
## pclass survived name sex age sibsp parch ticket fare
## <dbl> <dbl> <chr> <chr> <dbl> <dbl> <dbl> <chr> <dbl>
## 1 1 1 Allen, Miss. Elisabeth Walton female 29 0 0 24160 211.
## 2 1 1 Allison, Master. Hudson Trevor male 0.917 1 2 113781 152.
## 3 1 0 Allison, Miss. Helen Loraine female 2 1 2 113781 152.
## 4 1 0 Allison, Mr. Hudson Joshua Creighton male 30 1 2 113781 152.
## 5 1 0 Allison, Mrs. Hudson J C (Bessie Waldo Daniels) female 25 1 2 113781 152.
## 6 1 1 Anderson, Mr. Harry male 48 0 0 19952 26.6
## cabin embarked boat body home.dest
## <chr> <chr> <chr> <dbl> <chr>
## 1 B5 S 2 NA St Louis, MO
## 2 C22 C26 S 11 NA Montreal, PQ / Chesterville, ON
## 3 C22 C26 S <NA> NA Montreal, PQ / Chesterville, ON
## 4 C22 C26 S <NA> 135 Montreal, PQ / Chesterville, ON
## 5 C22 C26 S <NA> NA Montreal, PQ / Chesterville, ON
## 6 E12 S 3 NA New York, NYDoes the result look like data? Yes, it does. It is a data frame (see Section 3.6). More precisely, the command prints the only the first six lines of it, and it also does not show all the variables12 We can see data, both numbers and text, in columns, and these things seem to make sense.
Next, we should know how many rows (how many observations) are there in the dataset. This is a critical information–if the number is too small, we probably cannot do any analysis, if it is too large, our computer may give up.
The corresponding function in R is nrow (number of rows).
We show it in the tidyverse way
## [1] 1309The tidyverse-way of doing things will be more intuitive and easier to read when working with more complex analysis. Hence we mostly use the tidyverse style below. It can be understood as “take the titanic data, compute the number of rows”.
But whatever way we chose to issue the command, we find that the dataset contains data about 1309 passengers. This is good news–we expect the number of passengers on a big ocean liner to be in thousands. Had it been just a handful, or in millions, then something must have been wrong.
Another important question is the number of variables (columns)
we have in
data. This can be achieved with a very similar function ncol()
(number of columns):
## [1] 14So we have 14 columns (variables). Typical datasets contain between a handful till a few hundred variables, and usually we have at least some guidance of the dataset size. Here, if the number had been in thousands, it might have been suspicious. What kind of information could have been recorded about passengers so that it fills thousands of columns? After all, in 1912 all this must have been handwritten… But 14 columns is definitely feasible.
We may also want to know the names of the variables.
This can be done with the function names():
## [1] "pclass" "survived" "name" "sex" "age" "sibsp" "parch" "ticket"
## [9] "fare" "cabin" "embarked" "boat" "body" "home.dest"One can see that the variables include a few fairly obvious ones, such as “pclass”, “survived” and “age”. But there are also names that are not clear, such as “sibsp” and “parch”.
So far, everything looks good. But there is one more thing we should
check. Namely, sometimes the dataset is only correctly filled near
the beginning, while further down everything is either empty or
otherwise wrong. So we may also want to
check how the last few lines look like. This can be done with
tail(), for instance, we can print the last two lines as
## # A tibble: 2 × 14
## pclass survived name sex age sibsp parch ticket fare cabin embarked boat body
## <dbl> <dbl> <chr> <chr> <dbl> <dbl> <dbl> <chr> <dbl> <chr> <chr> <chr> <dbl>
## 1 3 0 Zakarian, Mr. Ortin male 27 0 0 2670 7.22 <NA> C <NA> NA
## 2 3 0 Zimmerman, Mr. Leo male 29 0 0 315082 7.88 <NA> S <NA> NA
## home.dest
## <chr>
## 1 <NA>
## 2 <NA>The two last lines also look convincing. These lines are printed in a
similar manner as the first lines, leaving out some variables, and
cutting short names. But what if the
beginning and end of the dataset are good, and all the problems are
somewhere in the middle? We may take a random sample of
observations in the hope that this will spot the problems. The
function sample_n() achieves this, for a random sample of 4 lines we
can do
## # A tibble: 4 × 14
## pclass survived name sex age sibsp parch ticket fare cabin embarked boat
## <dbl> <dbl> <chr> <chr> <dbl> <dbl> <dbl> <chr> <dbl> <chr> <chr> <chr>
## 1 2 0 Lahtinen, Rev. William male 30 1 1 250651 26 <NA> S <NA>
## 2 3 0 Assaf, Mr. Gerios male 21 0 0 2692 7.22 <NA> C <NA>
## 3 3 0 Wiklund, Mr. Karl Johan male 21 1 0 3101266 6.50 <NA> S <NA>
## 4 2 0 Sjostedt, Mr. Ernst Adolf male 59 0 0 237442 13.5 <NA> S <NA>
## body home.dest
## <dbl> <chr>
## 1 NA Minneapolis, MN
## 2 NA Ottawa, ON
## 3 NA <NA>
## 4 NA Sault St Marie, ONHere all looks good as well.
Note that the printout also includes variable types, these are the
<dbl> and <chr> markers underneath the column names. The most
important types are
<dbl>: number (double precision number)<int>: number (integer)<chr>: text (character) or categorical value<date>: for dates
Exercise 6.1 Load the titanic dataset using a wrong separator, <tab> instead of
comma as follows:
Display the first few lines and find the number of rows, columns and variable names.
See the solution
6.2.2 Are the relevant variables good?
Obviously, we do not need to check all variables in this way. If our analysis only focuses on age and survival, we can ignore all the other ones. It is also clear the we will not discover all the problems in this way, e.g. we will not spot negative age if it is rare enough.
A good starting point is often to just narrow the dataset down to just the variables we care about. But before we even get there we need to have an understanding about what it is we care about. So we should start with either a problem or a question that we try to address. For instance, when using the Titanic dataset we did above, we might consider the following questions:
Was survival related to passengers’ age, gender, class and home location?
Now we only need variables that are actually related to these characteristics.
In practice, though, it is also common to work in the other way–first you look what is in data, and based on what you find there you come up with interesting question. This seems somewhat a reverse process, but it is not quite true. In order to derive a question from data you need to know enough about potentially interesting questions. It is more like you have your personal “question bank”, and when you see a promising dataset, then you check if any of those questions can be addressed but the data.
Before we select relevant variables we need to get an idea what variables are there. First you should consult documentation (if such exists), but in any case there is no way around from just checking all the variables in data. This is because whatever is stated in the documentation may not quite correspond to the reality. We checked the variable names above, but let’s do it here again:
## [1] "pclass" "survived" "name" "sex" "age" "sibsp" "parch" "ticket"
## [9] "fare" "cabin" "embarked" "boat" "body" "home.dest"The variables that are relevant to answer the question above are survived, age, sex, pclass and home.dest. We can discuss others (e.g. embarked), or if passengers’ name tells us something relevant. But let’s focus on these five variables first.
Let us first scale the dataset down to just these five variables.
This can be done with select function:
The anatomy of the command is:
- take titanic data (
titanic) - select the listed variables (
select(survived, age, sex, pclass, home.dest)) - and store these as a new dataset called survival (
survival <-).
So now we have a new dataset called survival. A sample of it looks like
## # A tibble: 5 × 5
## survived age sex pclass home.dest
## <dbl> <dbl> <chr> <dbl> <chr>
## 1 1 39 female 1 Duluth, MN
## 2 1 38 female 1 New York, NY
## 3 0 40.5 male 3 <NA>
## 4 1 30 female 3 Union Hill, NJ
## 5 0 NA male 1 <NA>One can see that this dataset only contains these selected variables.
Note that here we created a new dataset survival. We could also have overwritten the original titanic data using command as
But this is often not a good idea–in case we want to go back to the original dataset and maybe include additional variables, we cannot do it easily. We have to go all the way up and re-load data. So we prefer to create a new dataset while also preserving the original one.
If we want to check a single variable only, then we can extract just
that one with pull:
## [1] 7.8958 15.5000 12.2875 7.8958 7.7500 7.5208 25.9292 26.0000 14.5000 13.5000What we did here was to first sample 10 random lines from the dataset
(otherwise it would print 1309 numbers). Thereafter we
extract the variable “fare” from the sample. R automatically prints
the numbers. Note that unlike select that returns a data frame,
pull returns just the numbers (a vector of numbers), not a data
frame. You can see this from how it prints it. For many functions,
such as mean, min, or range,
the plain numbers is what we need, data frame will not work.
But just looking for numbers is only a good strategy if the dataset is small. It is hard to find e.g. maximum or minimum values in even the Titanic datast (1309 observations), not to speak of datasets with millions of rows. Instead, we may use the built-in functions to do some basic analysis. For instance, let’s find the largest number of passenger class, “pclass”:
## [1] 3Here we extracted the variable “pclass” (just as a numeric vector, not data frame), and used the function “max” that returns the maximum value. So the larges class (lowest class) is 3rd class.
Exercise 6.2 Find the uppermost class (smallest class number). Use function min.
Exercise 6.3 What is the average survival rate? Use variable “survived” and
function mean.
Exercise 6.4 Find the age of the oldest passenger (variable “age”). What do you find?
6.3 Missing values
A pervasive problem with almost all datasets are missing values. It means some information is missing, it is just not there. There is a variety of reasons why some information may be missing–either it was not collected (maybe it was just not available), maybe it is not applicable, maybe it was forgotten at data entry… But in all those cases we end up with a dataset that does not contain all the information we may think it contains.
Missing values may complicate the analysis in a number of ways. First, although data documentation may state that data contains certain information (variables), a closer look may reveal that most of the values are actually missing. This usually means we cannot easily use those variables for any meaningful analysis.
Second, there may be a hidden pattern (selectivity) in missingness. For instance, when we conduct an income survey, who are the people who are most likely not to reveal their income? Although anyone may refuse to reveal this bit of personal data, it is more often the case for those who experience irregular income (e.g. entrepreneurs and farmers). In certain months or years they may earn a lot, other time very little. The may simply be unable to answer the question about their yearly income. And when we want to compute some figures, for instance the average income, then we just do not know if the number we found is close to the actual one. We may miss a particularly low, or maybe a particularly high income earners.
Missing values may be coded in different ways. R has a special value,
NA to denote missing (Not Available)13
R also has a number of methods to find and handle NA-s. But not all
missing values are coded as NA. For instance, it is common to just
denote missing categorical data by empty strings. In sociology, it is
common to code missing values as “9” or “99” or something similar,
given such values are clearly out of range. Alternatively, missings
can be coded as negative values. In those cases one has to consult
the codebook, and remove the missing values using appropriate
filters–missing values coded as ordinary numbers would otherwise
clearly invalidate the analysis.
Because missing values make most result invalid, one has to be careful
when doing calculations with data that contains missings. R enforces
this with many functions return NA if the input contains a missing.
Consider a tiny data frame
| age | income |
|---|---|
| 20 | 50 |
| 30 | 100 |
| 40 | NA |
This data frame contains two variables: age and income. All values for age are valid, but income has a missing value. We can easily compute mean age:
## [1] 30However, if we attempt to do the same with income, we’ll get
## [1] NAR tells us that it cannot compute average income as not all the values are known. If, instead, we want to compute average of known incomes, we have to tell it explicitly as
## [1] 75na.rm=TRUE mean to remove NA-s before computing the mean. This is a
“safety device” to ensure that the user is aware of missing values in
data. Admittedly though, it is somewhat inconvenient way to work with
data.
Obviously, this only works if missings are coded as “NA”. If they are coded as something else (e.g. missing income may be coded as “-1” or “999999”), then the safety guardrail does not work. It is extremely important to identify missing values, and adjust the analysis accordingly.
6.4 How good are the variables?
Before we even want to handle missing values somehow, we should have an idea how many missing values, or otherwise incorrect values do we have in data. If only a handful of values out of 1000 are missing, then this is probably not a big deal (but depends on what are we doing). If only handful of values out of 1000 are there and all other are missing–then the data is probably useless.
You get an idea of missingness when you just explore the dataset in the data viewer. But it is not always that easy–if the dataset contains thousands of lines, and missing values are clustered somewhere in the middle of it, then you may easily miss those. It is good to let R to tell the exact answer.
One handy way to do this is by using summary function. For
instance, let’s check how good is the age variable in data:
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## 0.1667 21.0000 28.0000 29.8811 39.0000 80.0000 263The summary tells us various useful numbers, in particular the last one: the variable age contains 263 missing values. So we do not know age of 263 passengers, out of 1309 in total (about 20%). Is this a problem? Perhaps it is not a big problem here (but depends on what exactly we do). Some other variables, however, do not contain any missings. For instance,
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.000 0.000 0.000 0.382 1.000 1.000The provided summary does not mention any missings–hence data here does not contain any unknown survival status.
If we do not want to get the full summary, we can do this by
## [1] 263The anatomy of the command is the following: we pull the variable
age out of the data frame. is.na() tells for every value there if
it is missing or not, and sum() adds up all the missing cases.
Exercise 6.5 Repeat the example here with survived. Do you get “0”?
But missingness in a sense of the variable being NA is not the only
problem we encounter. Sometimes missing values are encoded in a
different way, and sometimes they just contain implausible values,
such as negative price or age of 200 years (see Section
@ref(#r-preliminary-missings)).
For numeric variables, we
can always compute the minimum and maximum values and see if those are
in a plausible range. For instance, the minimum and maximum values of
age are:
## [1] 0.1667## [1] 80Exercise 6.6 What does the na.rm=TRUE do in the commands above? See Section
6.3 above.
The minimum 0.167 years (2 months) and maximum 80 years, are
definitely plausible for passengers. So apparently all the
non-missing age values are good because these must be inbetween of the
extrema we just calculated. If computing both minimum and maximum,
then we can also use a handy function range() instead the displays
both of these. Let’s compute the range of fare:
## [1] 0.0000 512.3292It displays two numbers, “0.0000” and “512.3292”. While the maximum, 512 pounds, is plausible, the minimum, 0, seems suspicious. Were there really passengers on board who did not pay any money for their trip? Unfortunately we cannot tell. Perhaps “0” means that they traveled for free as some sort of promotion trip? Or perhaps their ticket price data was not available for the data collectors? Or maybe they just forgot to enter it? It remains everyones guess.
But what if the variable is not numeric? For instance, sex or
boat are not numeric, and we cannot compute the corresponding
minimum and maximum value. What we can do instead is to make a table
of all values there, and see if all possible values look reasonable.
This can be done with the function table(). For sex we have
## .
## female male
## 466 843There are only two values, “male” and “female”, both of which look perfectly reasonable.
Exercise 6.7 Why may it not be advisable to use table for numeric variables? Try
it with fare. What do you see?
Besides the basic analysis we did here, we should also look at the distribution of the values (see Section 10.2.1) before we actually use these for an actual analysis.
6.5 What is not in data
Data analysis is often conveniently focusing on what is in data, and forgetting about what is not in data. Indeed, it is hard to analyze something that is not there. But this is often a crucial part of information.
Consider the following case: you are a data analyst, attached to the allied air force during WW2. Your task is to analyze the damage that to the bombers after their missions, and make recommendations about which parts of planes to add armor. As armor is heavy, you cannot just armor everything but it is feasible to add armor to certain important parts. You see there is a lot of damage in the fuselage and wings, but you do not see much damage in engines and the cockpit. Where would you place armor?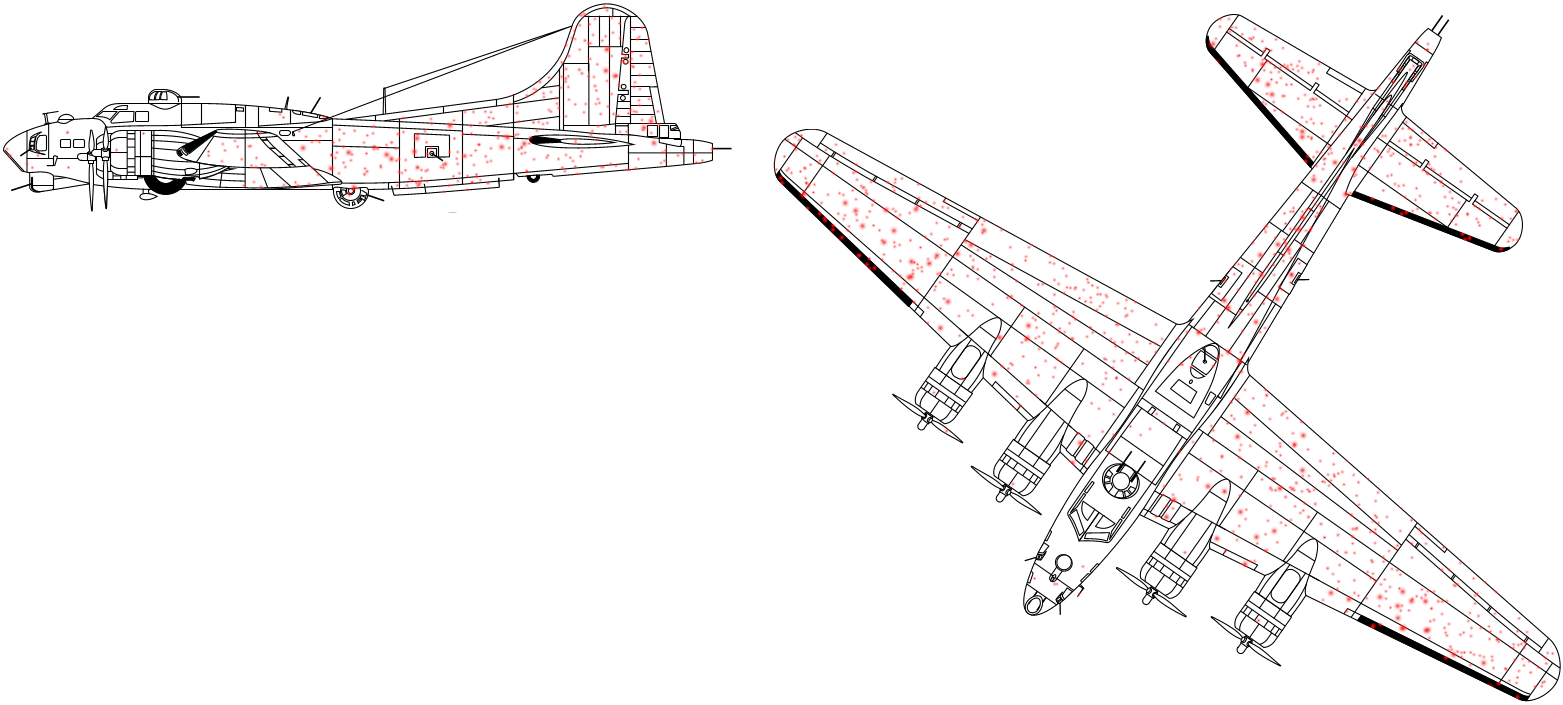
Damage on allied bombers (damage of all planes marked here by red dots on a single plane). There is a lot of damage in the fuselage and wings, but not much in the engines and cockpit.
What is missing in these data? A good way to start looking for what is missing is to ask how was data collected (how it was sampled). So how did we learn about damage to our bombers? Well, obviously be looking at the damage on the planes that returned from the mission. We collected the data by analyzing planes that returned, but we ignored the planes that did not return. (Obviously, there are good reasons for that.) But as a result, our data is not a representative sample of what we want to analyze. It may still be a sample of what may happens to the future planes that return from the mission. And if our task is to make the planes that return to look nice, then we should armor their fuselage and wings.
But if our task is to make more planes to return, then the conclusion is the opposite–planes that get damage in the engines or cockpit are not returning. So we should place armor there. Understanding of sampling completely reverses the conclusion.
6.6 Sampling, documentation
The previous example–what is not in data–is a more general case of sampling (See Section 3.4). It is easy to answer questions about a particular dataset. In the bomber example above, the answer involves the planes that returned. But most of the more relevant questions are not about any particular dataset but about a more general problem, such as about all planes or about other similar people. For instance, if you learn that an average data scientist in a particular dataset earns, say, $100,000 then it is somewhat interesting number in itself. But what does this number tell about all data scientists? What does it tell about you if you will choose to become one?14
In order to use data, a sample, for analyzing the more general problems (the population), we need to know how is the sample related to the population. We need to know how it is sampled. Note that we never can collect data about everything–even if we sample 100% of what we have (e.g. damage in all planes, including those that do not return), what we want is to improve the survivability of future missions. And we cannot collect data about the future. Instead, we have to assume that data we collected about the past tells us something about the future.
The sampling scheme that is easiest to work with is random sampling, i.e. where each case is equally likely to land in the sample, in our dataset. Well established statistical procedures exist to find the relationship between what we see in the sample, and how to total population will look like in that case. It is also fairly straightforward to work with cases where the sampling is not random, but the deviations are well documented and easy to understand. Such cases include, for instance, surveys where certain populations are oversampled. For instance, we survey 0.1% of total population, but because we are in particular interested in immigrants, we will sample 1% of immigrants. Now we have many more immigrants in the sample than we would otherwise have and hence we can get much better information about that group. But now we are working with a biased sample. Fortunately, it is very easy to correct for the bias (given we know who is immigrant).
But in many cases the sampling scheme is much less clear-cut. Consider, for instance, a poll of voters. Typically the pollsters call about 1000 voters and ask about their political preferences and voting intentions. This sample of 1000 is then used to tell something about all voter, i.e. we want to answer the question _who will win the elections?
What is the sampling scheme here? This is a subset of potential voters who the pollster can reach (they have the phone numbers), and who are willing to answer the question. How is this group related to all voters? We do not know well. We can guess that there are voters who do not have phones, or who have phones that pollster does not know. Or who refuse to answer. Or maybe they answer but do not reveal their actual intentions. Besides of that, people can change their minds, e.g. they only go to vote if it is not raining. All this is rather hard to take into account even if we mostly understand what are the problems. And hence we can see that different polls do not agree, and many pollsters may get their predictions utterly wrong.
But things get only more complicated when we start looking at “big data”. Some of big datasets are sampled using a well understood and simple scheme, e.g. science datasets like a census of all stars brighter than a certain magnitude. Data about humans, unfortunately, tends to be much much more messy. For instance, when predicting popular opinion based on twitter tweets we do not know well who are twitter users, how are those who tweet actually selected (most twitter users hardly ever tweet), and whether they actually express their true opinion. We just do not know. Hence conclusions based on twitter data always have the caveat that they are about “twitter users”, not about the general population.
In the best case the sampling is at least documented. For instance, when collecting twitter data, the documentation may explain how are the users and tweets sampled, even if we do not know how are they related to the general population. But there are plenty of datasets that lack any documentation whatsoever. You may get reasonable results, or maybe weird results, but as long as you do not know anything about the sampling, you should not use the results based on such datasets to make claims about the actual world.
This is what the “6 more variables: fare
, cabin , embarked , boat , body , home.dest ” below tells you↩ This is somewhat similar, but not the same as
NaN(Not a Number). NaN denotes not missingness, but a result of illegal mathematical operation, such as0/0.↩This is essentially the same as difference between descriptive statistics and inferential statistics. See Section 7.1.↩