A Introduction to Machine Learning
A.3 Overfitting

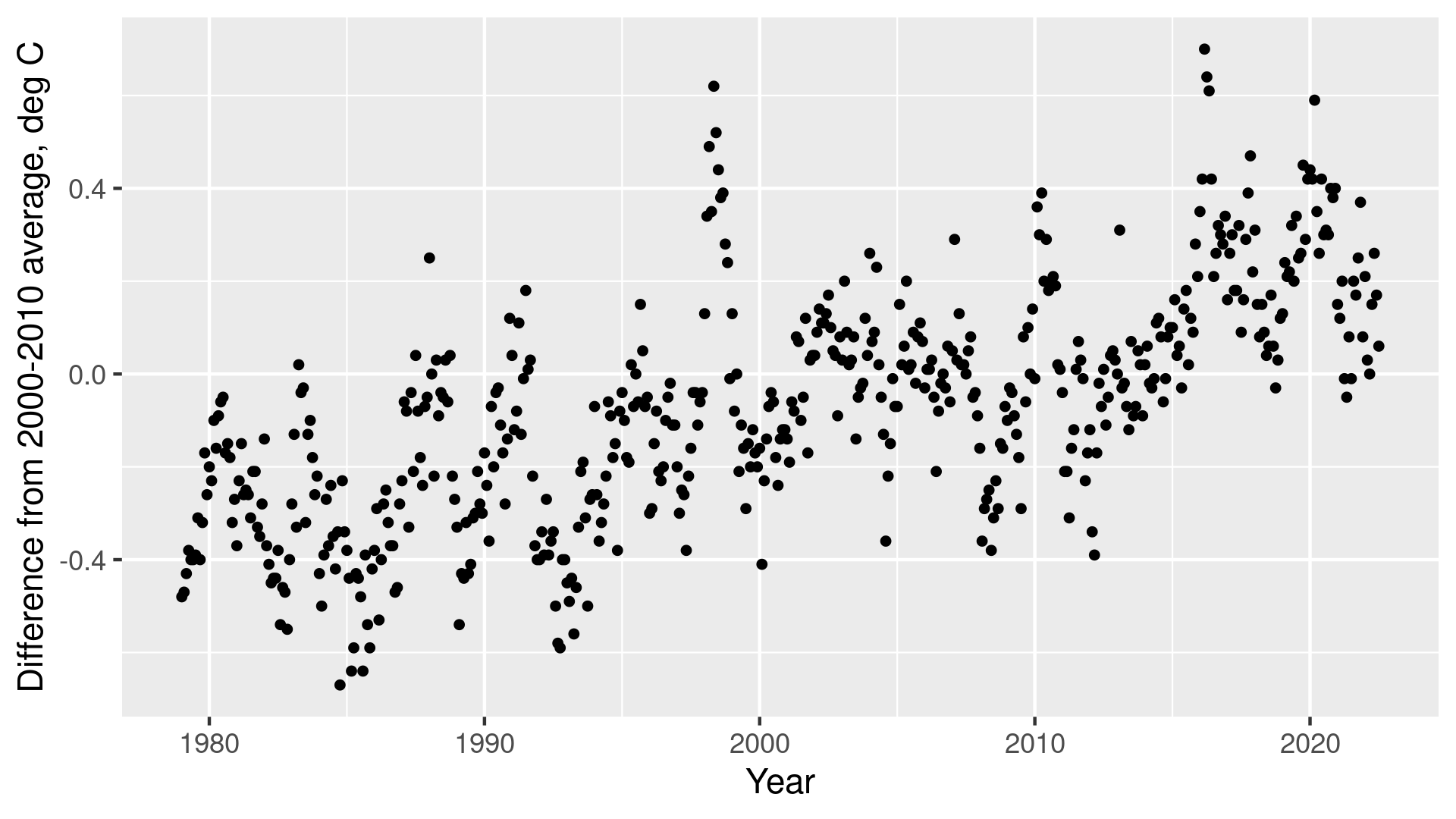
An example dataset.
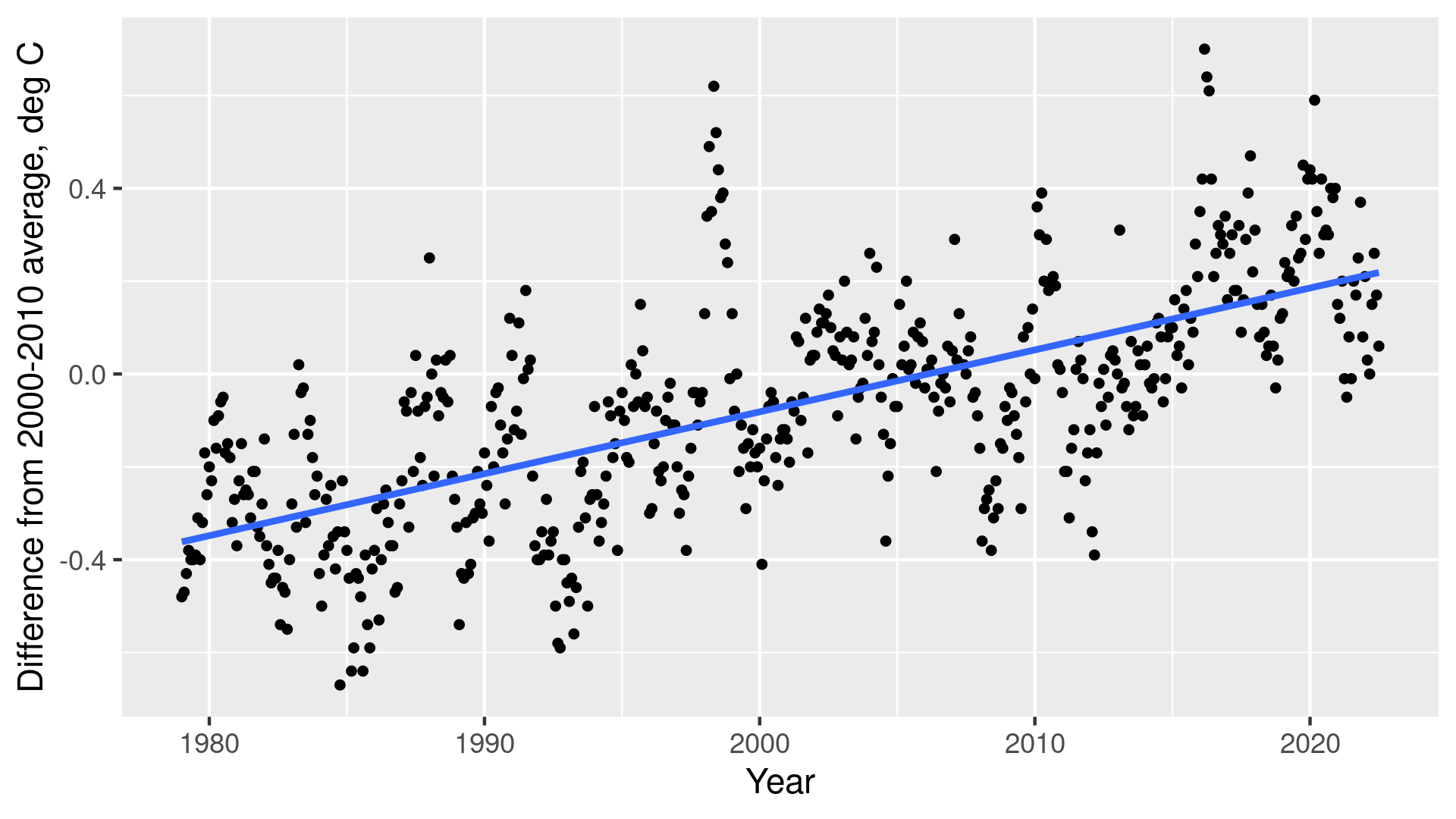
Consider data on the figure here. What might be a good model to describe the relationship between \(x\) and \(y\)? Without knowing much more, one may assume that a linear regression will do–the points seem to broadly follow an increasing linear trend. Obviously, if we model data using linear regression then we do not get exact results as data do not follow the trend very closely.
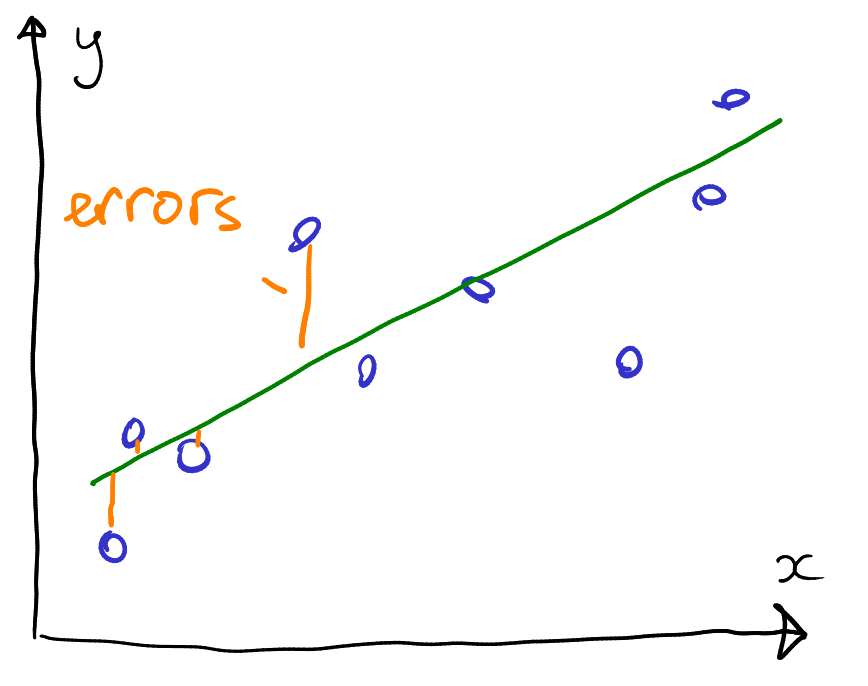
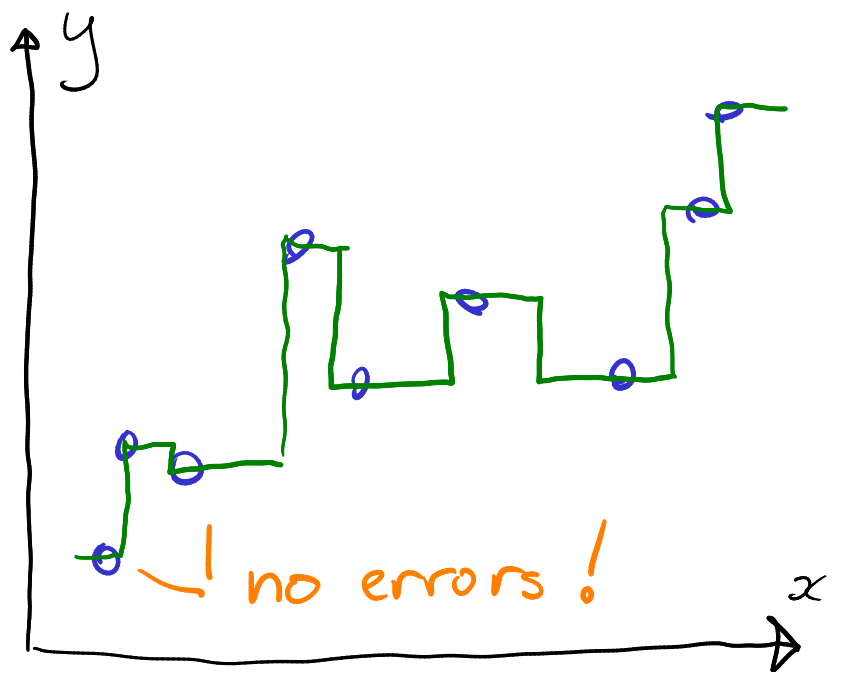
Modeling the same data with linear regression (left) and regression trees (right). While linear regression results in substantial prediction errors, trees can capture each datapoint perfectly. But are trees any better?
While trees may look like a superior method here, it is not that simple. The problem is related to what we want to use this model for. Indeed, if we know the values anyway, like what we see in these figures, then why do we need a predictive model in the first place? We make such models to predict values that we do not know, not those we already know. And it turns out that if that is what we want, then the excellent results of regression trees above may be wildly misleading.
Such behaviour–excellent results on known data–are often an indication of overfitting. Models may look super good on the dataset that was used for training, but on unknown data their performance may be very bad instead. This phenomenon is known as overfitting. It is a pervasive problem when using flexible models, such as trees, for doing predictive modeling. It is related to the models’ flexibility–too flexible models may pick up all kinds of patterns, not only those we are interested in. In this example, the tree did not just pick up the upward trend, but it figured out how to make a separate “step” for every single datapoint. It learned a too elaborate pattern.34 We need to test the model behavior on unknown data instead.
But how can we test how well does the model perform on unknown data? After all, these are the values we do not know, and hence we cannot say how well does the model predict those? Fortunately, there is an easy way around. Namely, the “unknown” datapoints should be unknown for the model, but they do not have to be unknown for us.
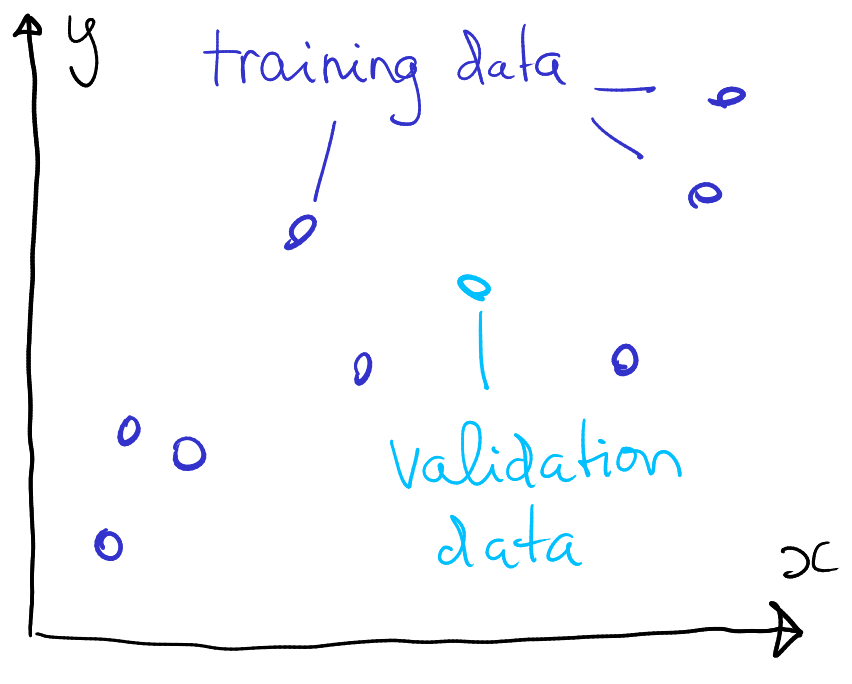
The same dataset, but now split into training (dark blue) and validation (light blue) chunks.
Consider the same data as above. But now we have decided that we will keep one of the points, the light blue “validation data”, unknown for the model. So the model will be trained with no information that there is, in fact, a value in this place. It will still do its best to fit all data points as well as possible, but now it cannot adjust itself for the validation data.
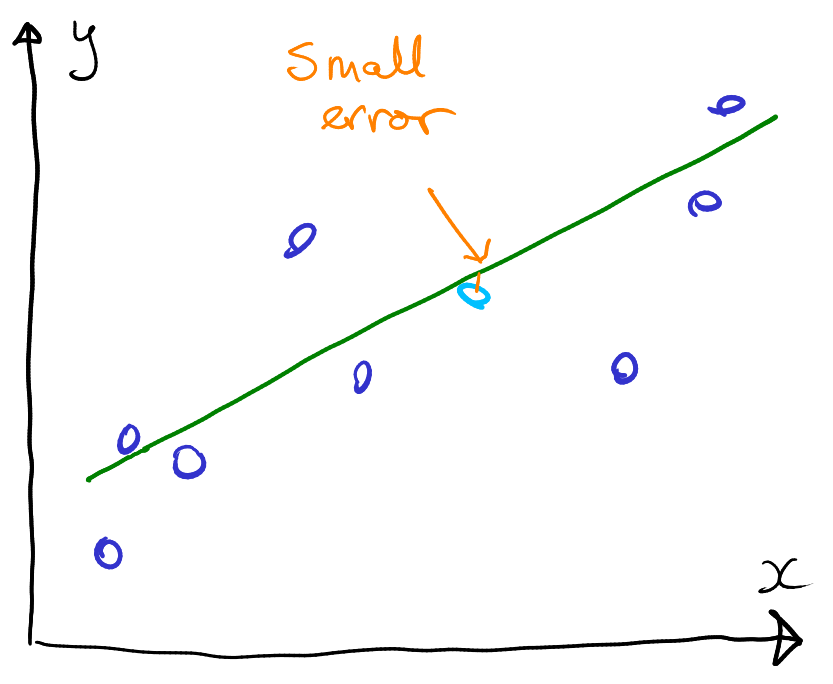
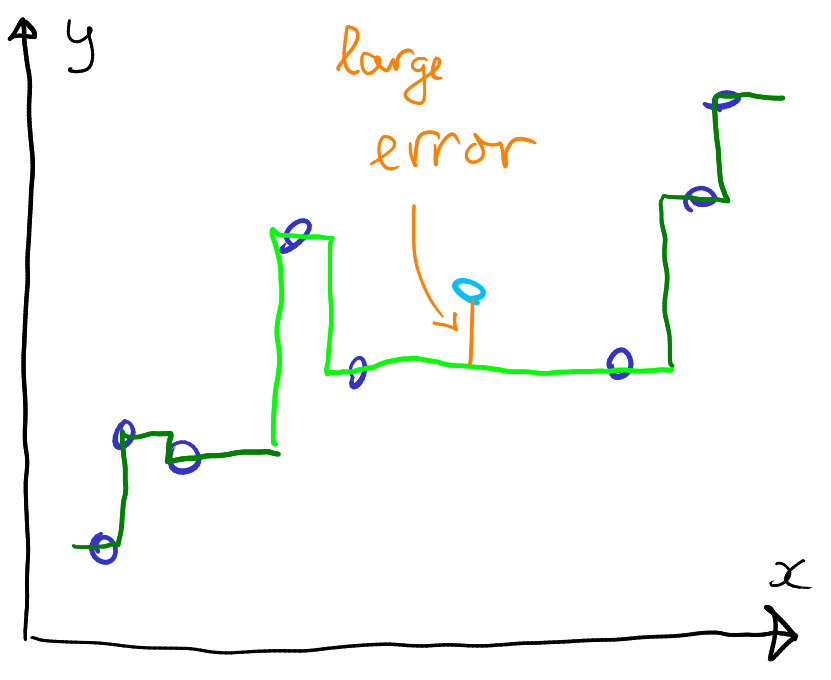
Separating data into regression and validation chunks. Validation data are data that are not “shown” to the model and only used afterward to test its performance. On these figures, validation error is larger for the tree.
This is a brief introduction to the idea of model validation, and using dedicated validation data for it. The main message is straightforward–if we care about the model performance on unknown data then we should measure it on unknown data.
Overfitting is typically not a problem with linear and logistic regression, as those are much more “rigid” models.↩︎