Key LPL model parameters In the LPL model (Curtis 1986), four key parameters determine the survival response of cells exposed to ionizing radiation. The four parameters are: - Initial DSB yield Gy-1 cell-1. Specify using the DSB={value} keyword.
- Initial yield of unrepairable (and thus fatal) lesions Gy-1 cell-1. Specify using the FL={value} keyword.
- 1st order DSB rejoining rate. Specify using the LAM={value} keyword or RHT={value} keyword. The LAM and RHT parameters are related by LAM = LN(2)/RHT.
- Rate of pairwise damage interaction (2nd order DSB rejoining rate). Specify using the ETA={value} keyword.
In addition to these four key radiosensitivity parameters, several other parameters can be adjusted to better reflect the biological properties of a particular type of cell, such as the DNA, NC, A0 (or B0), and GAM parameters. Refer to the Biophysical Parameters section of the manual for a complete list biological parameters and their definitions.
Tip: The widely used LQ survival formula, S = exp{-D(a + bGD)}, is a low dose and dose rate approximation for the LPL model. Here, D is the absorbed dose, G is the dose protraction factor that accounts for dose-rate and dose-fractionation effects, and a and b characterize intrinsic radiosensitivity. Estimates of LQ radiosensitivity parameters (a and b) derived from the LPL radiosensitivity parameters are reported in the VC output file.
Exercise 1 - Paste the contents of LPL sample file #1 into a new ASCII input file called lpl1.inp (see Getting Started on the Tutorial for help with this step).
- Modify lpl1.inp to generate several single-dose exposure scenarios. Setup scenarios to delivery absorbed doses from 0 to 10 G and deliver the doses at 1,000 Gy/hour).
- Generate survival curves for repair half-times (RHT parameter) of 0.25 h, 0.5 h, 1 h, 2 h, 4 h. Plot surviving fraction (y-axis, log scale) vs. absorbed dose (x-axis, linear scale). The plot should look similar to Figure 1.
Questions- Does the surviving fraction tend to increase, decrease or stay the same as the repair half-time increases?
- Does the LQ radiosensitivity parameter a change as the repair half-time changes (see VC output file for value of a)? If so, does a increase or decrease as the repair half-time increases?
- Does a/b ratio change as the repair half-time changes? If so, does a/b increase or decrease as the repair half-time increases?
Increase the DSB yield by a factor of two (DSB parameter). Does a increase, decrease or stay the same? Does a/b increase, decrease or stay the same? Identify a formula to relate changes in a and a/b to changes in the initial DSB yield.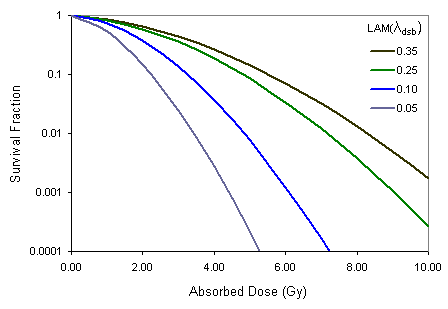 Figure 1. Effects of the DSB rejoining rate parameter LAM on cell survival.
Exercise 2- Create a copy of the lpl1.inp file (Exercise 1); rename the file to lpl2.inp.
- Change the dose rate from 1,000 Gy/hour to 0.01 Gy/hour.
- Set the half-time for DSB rejoining to 4 h. Plot surviving fraction (y-axis, log scale) vs. absorbed dose (x-axis, linear scale).
Questions - Re-run the simulation with repair half-times of 0.1 h, 0.5 h, and 2 h. Is the survival response of this cell sensitive to the value of RHT (and hence LAM) under low dose rate exposure conditions?
- Set the repair half-time to 2 h and then re-run the simulation with values of ETA equal to 10-5 h-1 and 10-
3 h-1. Is the survival response of this cell sensitive to the value of ETA under low dose rate exposure conditions?Increase the initial yield of fatal lesions by a factor of 2 (FL parameter). Is the survival response of this cells sensitive to the value of the FL parameter?Determine a formula to estimate FL from the surviving fraction S for low dose rate exposure conditions. Hint: The LQ protraction factor, G, approaches zero for very low dose rates so that S ~ exp{-aD}. Solve for a (which is related to the FL parameter). Will estimates of FL be too high or too low if a survival fraction for an acute exposure (high dose rate) is used instead of survival data for a low dose rate exposure conditions?
Exercise 3- Create a copy of the lpl1.inp file (Exercise 1); rename the file lpl3.inp.
- Set the dose rate to 25 Gy/h.
- Set the repair half-time equal to 0.25 h (RHT=0.25). Then set ETA = LN(2)/(RHT*1000). Plot surviving fraction (y-axis, log scale) vs. absorbed dose (x-axis, linear scale).
- Repeat step 3 for repair half-times of 0.75 h, 2 h, and 4 h, i.e., compute ETA for each repair half-time using the formula ETA = LN(2)/(RHT*1000), run the simulation and then add the survival curve to the plot. Upon completing step 4, the plot should have four curves (one for each combination of RHT, ETA).
Questions- Compute the ratio of LAM/ETA for each of the repair half-times (compare to value reported in VC output file). Does this ratio increase, decrease or stay the same as the repair half-time increases (this is not meant to be a trick question; the answer is readily apparent if you think about the method used to compute ETA from the RHT)?
- Does the value of a increase, decrease or stay the same as the repair half-time increases?
- Does the value of a/b increase, decrease or stay the same as the repair half-time increases?
- Are changes in a and a/b proportional to the repair half-time or the ratio LAM/ETA?
|
