29.1 Aquatic Dynamics
29.1.1 Equations
Here, we start with the equation for adult ecology from before, leaving out parasite transmission dynamics. We modify the basic slightly by adding one extra term that describes delayed maturation, a different response to crowding [89]. The mosquito maturation rate, \(\psi e^{-\sigma L}\) defines the average time from egg to emergence, and we add one parameter that slows down larval development in response to crowding. The per-capita mortality rate, \(\psi + \theta L\), has two parts: a density independent term \(\psi\) and a response to mean crowding \(\theta L\). We assume that adults lay \(\chi\) eggs per feeding cycle.
\[\begin{equation} \begin{array}{rl} \frac{dM}{dt} &= \Lambda - g M\\ \\ \hline \frac{dL}{dt} &= \eta - (\psi e^{-\sigma L} + \phi + \theta L) L \\ \Lambda &= \frac{1}{2} \psi L e^{-\sigma L}\\ \eta &= \chi f M \\ \end{array} \end{equation}\]
29.1.3 Regulation
This code solves the equations:
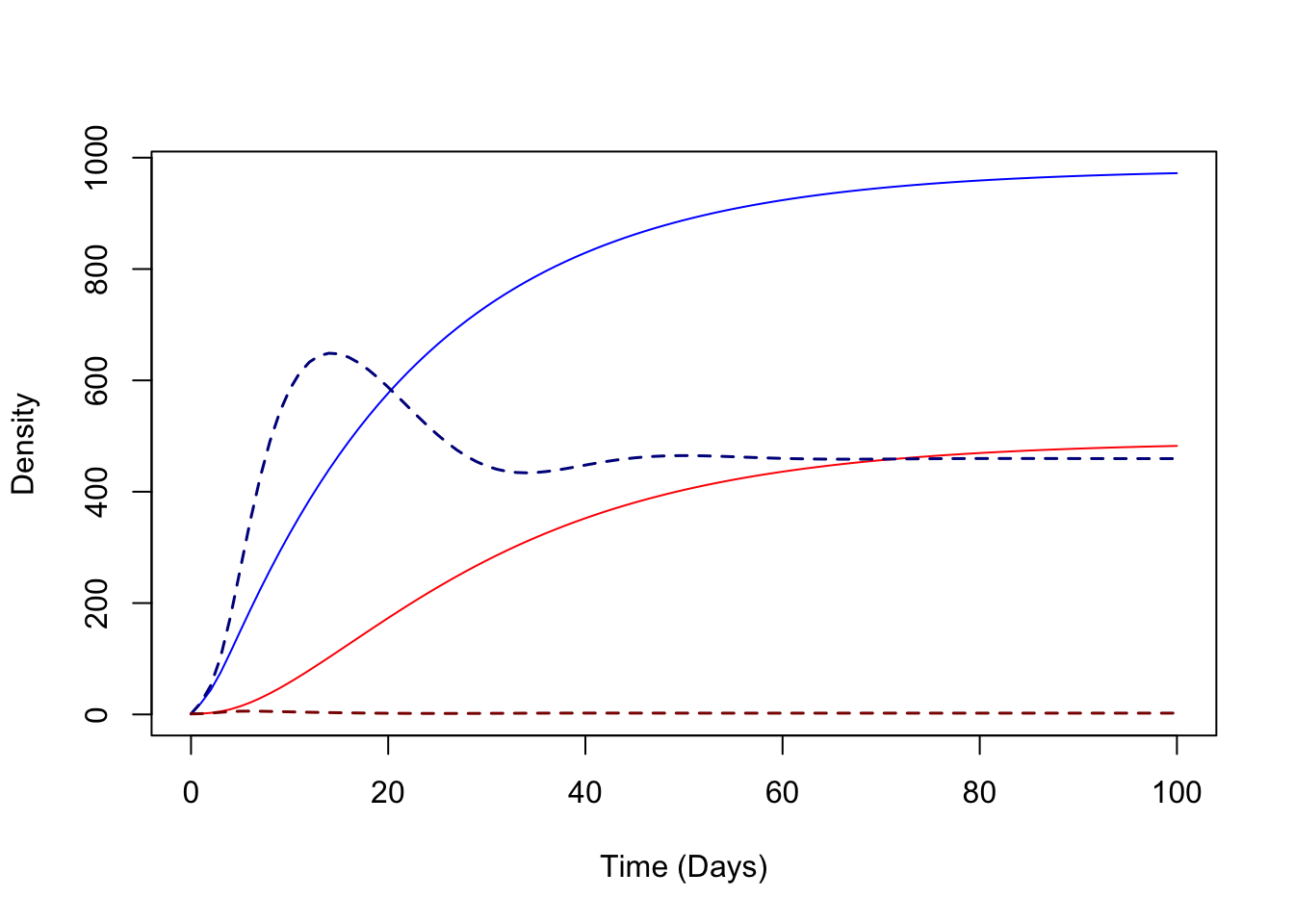
The first thing to point out is that changing the dynamics take some time to approach equilibrium – a couple of months, in this model. The second is that increasing mortality rates for mosquitoes in aquatic habitats by a factor of 10 affects the mosquito densities in minor ways.

The third is that increasing the response to mean crowding has a very strong effect on the population dynamics.
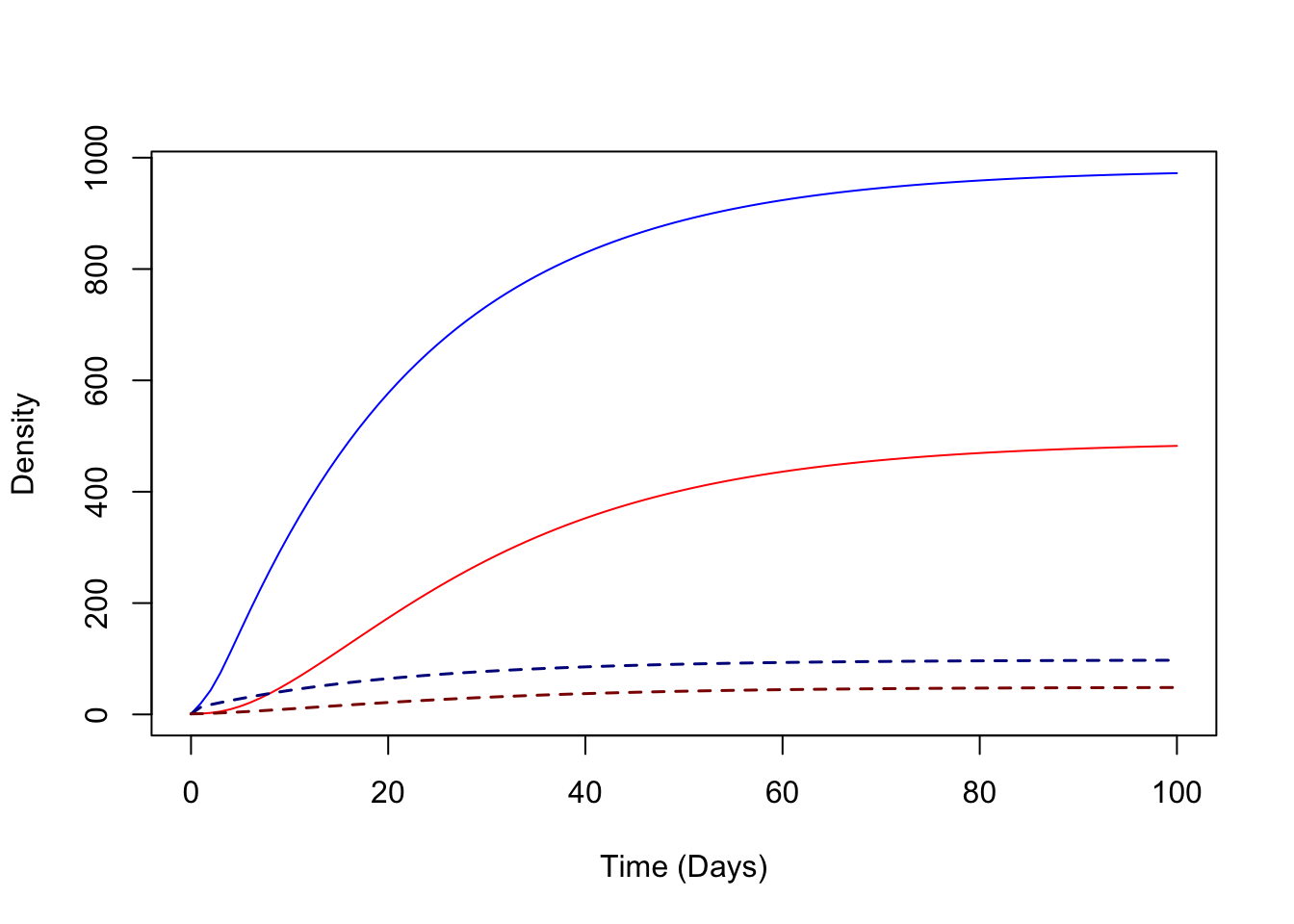
The third point is that density dependent responses to mean crowding cause much larger changes to this system than density-dependent mortality. Aquatic dynamics have a strong tendency to oscillate, but more critically, delayed maturation strongly affects the ratio of adult mosquitoes to adults.