10.1 Emergence
10.1.1 Variables
Aron & May, 1982
We define the following variables:
\(M\) is the density of mosquitoes.
\(Y\) is the density of infected mosquitoes.
\(Z\) is the density of infectious mosquitoes.
\(X\) is the density of infected humans.
In dynamical systems, we ask how the variables (i.e. \(M\), \(Y\), \(Z\), and \(X\)) change over time. In the following, we describe the changes on variable about a time.
For our first equation, we start with adult, female mosquito populations. (It is tiresome to repeat adult, female each time, and we’re ignoring male mosquitoes at this point anyway, so mosquito hereafter means adult, female mosquito, unless we say otherwise.) The number of mosquitoes is changing as new adults emerge from aquatic habitats or die.
To model changes in \(M\), we assume the following:
mosquitoes emerge from aquatic habitats at the rate of \(\Lambda(t)\) adults, per day;
mosquitoes die at a constant rate, \(g\). This is equivalent to assuming that the mosquito lifespan is exponentially distributed with a mean \(1/g\). The fraction surviving one day is \(e^{-g}\).
Our first equation describes changes in the number of mosquitoes:
\[\begin{equation} \frac{dM}{dt} = \Lambda(t) - g M \end{equation}\]
10.1.2 Blood Fed Mosquitoes
At this point, we will take a detour and define a variable describing the density of mosquitoes that have blood fed at least once, \(V\). After blood feeding, a mosquito is either gravid or parous, meaning its ovaries are distended from laying an egg batch. We do this, in part, because the fraction of mosquitoes that are parous is routinely collected, and because it gives us a chance to focus on blood feeding.
To describe blood feeding, we assume the following:
mosquitoes blood feed at the rate \(f\), per mosquito, per day; in this model, this implies that the waiting time to a blood meal is \(1/f\) days.
a fraction of all mosquito blood meals, \(q\), is taken on humans; we call this the human fraction
the human blood feeding rate is the product of these two parameters, \(fq\), which is defined as the number of human blood meals, per mosquito, per day.
The number of human blood meals by a population of vector mosquitoes, per person, per day is called the human biting rate (HBR). In this model, HBR is given by a formula:
\[\mbox{HBR} = \frac{fqM}{H}\]
Later, we discuss the correspondence between the HBR in models and data.
\[\begin{equation} \frac{dY}{dt} = f q (M-Y) - g V \end{equation}\]
We won’t use \(V\) to describe the dynamics of infection, but we might find it useful to understand how parity changes in mosquito populations.
10.1.3 Infected Mosquitoes
Mosquitoes become infected after blood feeding on an infectious human. To model changes in \(Y\), we extend the model of blood feeding to include infection. We need to know what fraction of blood meals end up infecting a mosquito that has not already been infected.
To model changes in \(Y\), we need to describe infection rates. We assume the following:
- a fraction of human blood meals, infects mosquitoes. We call this quantity net infectiousness (NI) and (for reasons that we will discuss in a moment), we give it a name, \(\kappa\):
\[\begin{equation} \kappa(t) = c \frac{X(t)}{H} \tag{10.1} \end{equation}\]
- infected mosquitoes die at the same rate as uninfected mosquitoes.
We can now write down our second equation describing changes in the number of infected mosquitoes:
\[\begin{equation} \frac{dY}{dt} = f q \kappa (M-Y) -g Y \end{equation}\]
10.1.4 Infectious Mosquitoes
To become infectious, a mosquito has to become infected and then survive through the extrinsic incubation period (EIP). We assume:
mosquitoes become infectious after a fixed delay, \(\tau\) days, called the EIP. The fraction of mosquitoes that survive through the EIP is \(e^{-g \tau}\).
infectious mosquitoes die at the same rate as other mosquitoes.
For a mosquito to become infectious, it must have become infected \(\tau\) days ago and survived through \(\tau\) days with probability \(e^{-g\tau}\). To write this in equations, we use a subscripted \(\tau\) to denote the value of a variable (\(M\), \(Y\) or \(X\)) or term (\(\kappa\)) at time \(t-\tau\). For example \(X_\tau\) is the number of people who were infected and infecious at time \(t-\tau\), and \(M_\tau\) is the number of mosquitoes at time \(t-\tau\).
The number of infectious mosquitoes that are added to the population at a point in time includes all the mosquitoes that became infected at time \(t-\tau\) and survived the EIP. This is our third equation describing changes in the number of infectious mosquitoes:
\[\begin{equation} \frac{dZ}{dt} = f q \kappa_\tau (M_\tau-Y_\tau) e^{-g\tau} -g Z \end{equation}\]
Here, \(Z\) represents the number of mosquitoes with sporozoites in their salivary glands. The fraction of mosquitoes with sporozoites in their salivary glands has been called the sporozoite rate (SR), which in our notation is
\[ z = \frac{Z}{M}\]
The number of bites by vector mosquitoes, per person, per day is called the entomological inoculation rate (EIR). It is defined as the product of the HBR and the SR:
\[\mbox{EIR} = \mbox{SR} \times \mbox{HBR}\]
In our notation, the EIR is:
\[\mbox{EIR} = z \frac{fqM}{H} = \frac{fqZ}{H}\] As with the HBR, we would like to know how to connect estiamted values of the EIR to our formulas. Since that’s really complicated, we’ve spent a lot of time in the following sections discussing it.
10.1.5 Infected Humans
Humans become infected after being bitten by an infectious mosquito. We assume the following:
A fraction \(b\) of all bites by infectious mosquitoes cause an infection.
The hazard rate for infection, also called the force of infection (FoI) and denoted \(h\) is \(b \times\) EIR: \[h = fqb \frac{Z}{H}\]
Infections clear at the rate \(r\), per infection, per day (the average time to clear is \(1/r\) days), and after clearing an infection a person becomes susceptible to infection again.
We can now write down our fourth equation describing changes in the number of infected humans:
\[\begin{equation} \frac{dX}{dt} = h (H-X) - r X \end{equation}\]
10.1.6 …as a System
While we presented these equations one at a time, they work as a system. To see it all at once, we write it here as a system with four equations and two terms:
\[\begin{equation} \begin{array}{rl} \frac{dM}{dt} &= \Lambda(t) - g M \\ \frac{dY}{dt} &= fq\kappa(M-Y) - g Y \\ \frac{dZ}{dt} &= fq\kappa_\tau(M_\tau-Y_\tau)e^{-g\tau} - g Z \\ \frac{dX}{dt} &= h (H-X) - rX \\ \\ \hline \\ \kappa &= c \frac{X(t)}{H} \\ h &= b fq \frac{Z(t)}{H} \\ \end{array} \end{equation}\]
![A diagram of the a version of the Ross-Macdonald model, using equations from Aron and May [59]](Figures/AronMay.png)
These equations describe processes in three domains (Figure 2.1):
adult mosquito ecology (\(M\), and perhaps \(V\));
parasite infection dynamics in mosquito populations (\(Y\) and \(Z\));
parasite infection dynamics in human populations (\(X\)).
The equations describing parasite infections in mosquito populations also include the variable \(M\), so the mosquito infection dynamics are coupled to the mosquito population dynamics. The way we’ve written the equations, each compartment has an input term (i.e., \(\Lambda\), \(\kappa\), or \(h\)) that depends on something else. We’ve passed \(\Lambda\) as a parameter. For the infection dynamics, the terms \(\kappa\) and \(h\) couple two separate systems. For adult mosquito dynamics, emergence is passed to the model as a parameters.
There are, of course, more compact ways of writing these equations. We have written the equations this way to emphasize a few things. First, the terms make it clear exactly how the equations in one domain are connected to another. Second, if we wanted to start changing some of the assumptions, these terms help to isolate the parts we might like to change. By writing the equations in this modularized form, we can start to understand how we might be able to write software that would allow us to represent mosquito infection dynamics with different systems of equations.
The next step is to find solutions.
NOTE: We don’t introduce exDE or MicroMoB until Modularity and Software.
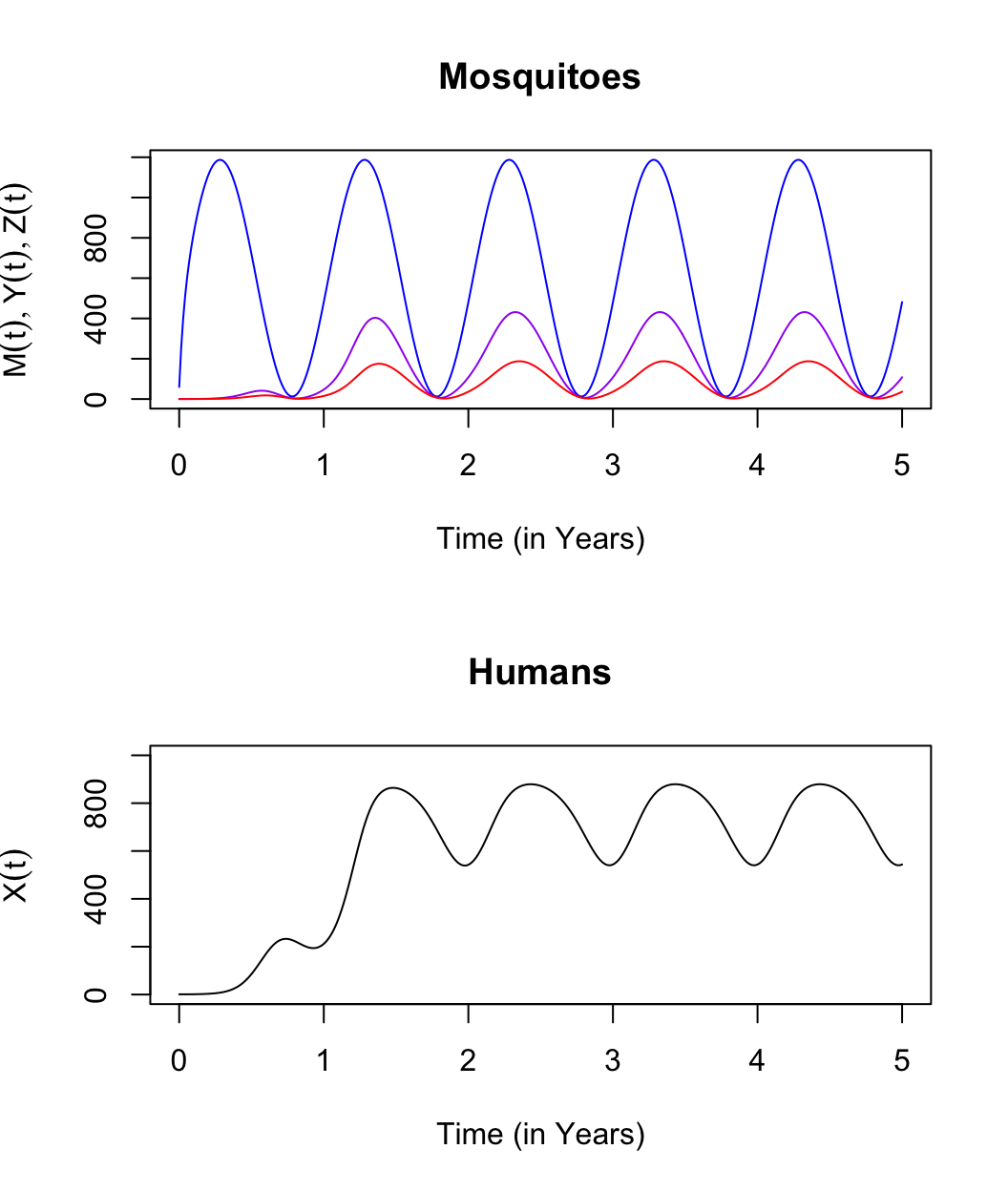
10.1.7 Solutions
What does a solution to these equations look like?
Solutions to these equations are values of the variables over time \(\left( M(t), Y(t), Z(t), X(t) \right)\) that satisfy the system of four equations described above. We call these solutions orbits. To put it another way, if we took the derivatives of the orbits for any variable at any point in time using the basic definition \[\lim_{h\rightarrow 0} \frac{x(t+h)-x(t)}{h},\] and then we used the values of the variables at time \(t\) to compute \(dM/dt\), \(dY/dt\), \(dZ/dt\), and \(dX/dt\) (i.e., using the formulas), we would get the same values.
It is important that these orbits are unique: after specifying the initial values of the variables, there is one and only one set of orbits that solves the equations. When we solve the equations, we usually produce solutions from a starting point into a future, but the orbits are defined for all time – \(i.e.\) the process implies the existence of solutions far back into the past. These are deterministic equations, after all.
As written, the equations do not define a model. Instead, the equations define a process or a model family. A model is something that can produce orbits. A model is defined only after assigning specific values to the parameters. Informally, we will often slip and use the “model” to describe a model family. It’s easy to slip up, and sometimes we can get by with being sloppy, but we need to remember the distinction. When we say that the software is modular, we mean that it is easy to swap out one model family for another.
To find solutions of equations we use an R software package called deSolve. Because of the delay for the EIP, these are called delay differential equations, which are handled using a function called dede. An important step in solving delay differential equations is a function lagvalue() that computes and returns the values of variables at a time lag, \(\ell\). In these equations, the lag is set by the EIP, \(\tau\), so we must evaluate
lagvalue(t-tau).
In solving ordinary differential equations, we must pass initial conditions. To solve a delay differential equations with a maximum lag \(\ell\), we must specify the initial conditions for the interval \([-\ell, t_0)\), where \(t_0\) is the point in time when we start computing solutions. In these equations, since the equation for \(dZ/dt\) looks back \(\tau\) units, we must specify values of \(M(t)\), \(Y(t)\), and \(X(t)\) for all values of \(t \in [-\tau, t_0)\). This forces an awkward choice, since we don’t know the solutions backwards in time, but would need to know those solutions to use them. What is typically done – and we’ve done it here – is to specify a constant set of initial values and moving on.
Doing this introduces a little numerical slop. By slop, we mean that these values are not what we would get if we ran the equations backwards in time. In these equations, it won’t affect our analysis most of the time, so we’re happy to acknowledge this little problem and find ways around it. It’s a little thing, but we should never forget it, because we might find that it is affecting our analysis at some point.
With deSolve, solving differential equations is not difficult – it just involves following a few steps. In the following, we walk through these steps:
Write a function that computes the derivatives;
Define initial conditions;
Define the values of the parameters;
Define a mesh on time;
Call a function that solves the equations, such as
dedefor delay differential equations.
Many users will find that reading this code is like learning how to compute \(\sqrt{2}\). If so, feel free to learn it once and then skip it.
10.1.7.1 Derivatives
The first step is to write down the equations to compute the derivatives. The solver expects a function with three required arguments (in this order):
tis timeyis the list of variablesparamsis a set of parameters
The derivatives are computed and returned in the same order as ‘y’ in a list. To make code that is easy to read, we make params as a list with parameter names (see below), so that inside the function with(params,{...}), the parameter names are visible.
10.1.8 Initial Values
To run the model, we must supply initial values. If you were writing code yourself, it would be important to remember that the initial values and the return value for the derivatives must occur in the same order.
A useful convention in {R} is to pass the initial values as a named list. Later, we can turn the outputs into a data frame, and then we can retrieve the variables by name.
The object y0 is a named list – the names are attached but invisible.
## M Y Z X
## 60 0 0 1When we turn it into a list, with as.list, the names are attached to the values:
## [1] 60If we use with, we create an environment where we can simply use the names:
## [1] 6010.1.9 Parameter Values
We pass the parameters as a list. It might seem like overkill, but we have written a function makeParams() that takes default values and generates a list. This makes it easy to generate a new set of parameter values with alternative values, and it also helps us to write and pass function \(\Lambda(t)\) with parameters we like. By passing the parameter as a list, the parameter values are available to the function dAronMay when we use with(params, {}).
Note that we have also attached the initial values of the variables as a parameter set, which are the return values for lagvalue(t) when t<0.
To make it absolutely clear, we are assuming:
\(g=1/12\): mosquitoes live about \(12\) days, on average
\(f=1/2.5\): mosquitoes feed every 2.5 days, on average
\(q=0.95\): the human fraction is 95%; mosquitoes feed on humans 95% of the time
\(c=0.15\): about 15% of bites on infectious humans infect a mosquito
\(b=0.55\): about 55% of bites by infective mosquitoes cause an infection
\(r=1/200\): human infections last about \(200\) days, on average
\(H=1000\): we’re simulating transmission in a population of a thousand humans
\(\tau=10\): the extrinsic incubation period is about 10 days
For emergence, we tune the average value using \(m\) and it is scaled to \(H\):
The parameter \(m\) in the function above has been set to \(0.05\) by default.
The parameter \(ss\) affects the amplitude of the fluctuations. We force it to take on values between 0 and 1.
Emergence is modeled as a sinusoidal function with a yearly cycle.
\[\Lambda(t) = m H \left(1 + \sin \left(\frac{2\pi t}{365}\right)\right)\]