2.2 Deterministic, Discrete-Time
The parts of a model: variables, parameters, initial conditions.
In this section, we present the basic, deterministic, discrete-time model for a mosquito-transmitted pathogen. Because it is the first model in the book, we’ll take the time to explain some background material in detail. We’ll discuss the parts of a model, and we walk through the process of solving models.
2.2.1 Model
We will present the parts of the model first, and write down the equations last. The parts of a model are called parameters and variables. To solve the model, we will need initial conditions for the variables. As we go, we will also write R code that implements the model and that solves it. In writing the code, we will adopt some conventions that we can use to help us write good code.
Variables are quantities that describe the state of a system. One variable in this model is time, denoted \(t.\) The dependent variables are the quantities that we want to compute, and they are computed at various time points. Time is marching forward, unaffected by the dependent variables, so we call it the independent variable.
In this model, there are two dependent variables: the proportion of humans and mosquitoes that are infected at each point in time. Since it is a discrete time system, the values of the variables are defined only at integer values of \(t.\) We define the variables as follows:
let \(t\) represent time, in days;
let \(x_t\) be the fraction of people who are infected at time \(t,\) and \(0 \leq x_t \leq 1;\)
let \(y_t\) be the fraction of mosquitoes who are infected at time \(t,\) \(0 \leq y_t \leq 1.\)
Another term for the fraction of a population that infected with parasites is prevalence.
Initial Conditions are the values of the variables at one point in time. Since the values of our variables in the next time step (at time \(t+1\)) depend on their values now (at time \(t\)), we can’t really compute anything specific unless we specify the values of the variables at one point in time. Having set one set of values, we can use the equations to compute the rest.
The initial conditions specify the values of all our variables at the beginning of the simulation. By convention, this is usually at time \(t=0,\) but we could also specify their values at any other point in time.
We can now begin to write R code to set up the objects so we can compute them. We set these initial values to be small:
## t x y
## 0.000 0.010 0.001In R, this object xy is called a named vector. The names that appear above the numbrers are carried along but they don’t affect the values of any computation done with xy. It is also useful that the names often get inherited (but not always). The names can be used as names using the function as.list() or data.frame().
## [1] 0.01When combined with the with() function, we can create a context where we can call them by name:
## [1] 0.01This code has adopted the convention of using named vectors so that we can write functions in a way that is easy to read. It also makes it easier to deal with the model outputs.
Parameters are quantities – rates, numbers, or probabilities – that describe some part of the process. Unlike variables, parameter values are chosen outside of a model and passed to it. In ross_diffs_1, these parameters are constant. Since they are constant, we call this an autonomous system of equations. In other models, we could have parameter values that changes over time, so the system would be called non-autonomous.
The parameters in this model define changes in prevalence: the fraction of humans that clear an infection each day; the fraction of infected mosquitoes that die; and blood feeding and infection.
Let \(s\) denote the fraction of people who clear infections after one day; \(0 < s < 1.\)
Let \(u\) denote the fraction of mosquitoes who die in one day; \(0 < u < 1.\)
Let \(a\) denote the fraction of mosquitoes who blood feed on a human in a day; \(0 < a < 1.\)
Let \(m\) denote the number of mosquitoes per human; \(m \geq 0.\)
# INPUTS
# s - The fraction of infections that clear each day
# u - The fraction of mosquitoes that die each day
# a - The fraction of mosquitoes that blood feed on a human each day
# m - The number of mosquitoes per human
#
# OUTPUTS
# a list with the parameter values by name
ross_dts_makepars = function(
s = 1/200,
u = 1/10,
a = 1/4,
m = 2
){
list(s=s, u=u, a=a, m=m)
}Equations describe dynamic changes in the variables over time. In this case, the process is described by a system of coupled difference equations.
Finally, we put all this together into a mathematical statement that has translated the description of a process, that are describe the process.
\[\begin{equation} \begin{array}{rl} x_{t+1} &= x_t - s x_t + m a y_t (1-x_t) \\ y_{t+1} &= y_t - u y_t + a x_t (1 - y_t) \\ \end{array} \tag{2.3} \end{equation}\]
We could rewrite the equations to make it easier to interpret them.
\[\begin{equation} \begin{array}{rl} x_{t+1} - x_t &= - s x_t + m a y_t (1-x_t) \\ y_{t+1} - y_t &= - u y_t + a x_t (1 - y_t) \\ \end{array} \tag{2.4} \end{equation}\]
In this alternative way of writing down the equations, the left hand side is interpreted as the daily change, and the terms on the right hand side describes those changes. The RHS has four terms:
\(- s x_t\) – is a decrease in the prevalence of human malaria infections caused by clearance of human infections: the fraction of humans who are infected is \(x_t\); a fraction \(s\) clears infections each day.
\(+ may_t (1-x_t)\) – is an increase in the prevalence of human malaria infections caused by the bites of infectious mosquitoes: the fraction of humans who are not infected is \(1-x_t\); a fraction \(m a y_t\) gets infected.
\(-u y_t\) – is a decrease in the prevalence of mosquito malaria infections caused by mosquito mortality: the fraction of mosquitoes who are infected is \(y_t\); a fraction \(u\) die.
\(+ a x_t (1-y_t)\) – is an increase in the prevalence of mosquito malaria infections caused blood feeding on an infected human: the fraction of mosquitoes who are not infected is \(1-y_t\); a fraction \(a x_t\) blood feeds on an infected human and gets infected.
To foreshadow something we will address in sub-section 2.4.2, if \(may_t >1,\) then it is not a proportion, and the equations don’t make sense.
To update the variables, we write a function in R. Since we will be developing a lot of functions and models, we adopt a simple naming convention: since it was developed by Ross, we attach the stem ross; since this is a discrete time system, we attach the suffix dts; we might want to generate other variants, so we append a number. The function is thus called ross_diffs_1.
# INPUTS
# xy - current variables, as a named vector
# params - the parameters, as a list
#
# OUTPUTS
# the updated values of the variables, as a named vector
ross_diffs_1 = function(xy, params){
with(as.list(xy),
with(params,{
xn = x - s*x + m*a*y*(1-x)
yn = y - u*y + a*x*(1-y)
return(c(t=t+1, x=xn, y=yn))
})
)
}2.2.2 Solutions
With the R code we developed, we can solve the equations, which involves computing the values of the variables iteratively. Since the values of the variables change, we create another object xy_t that we can use to store the values of computed variables over time.
## t x y
## 0.000 0.010 0.001We iterate in two steps. First, we compute the values.
Since we initialized the system at time \(t=0,\) the following computes the values of the parameters at time \(t=1.\) We can take a peak at the values we computed:
## t x y
## 1.0000000 0.0104450 0.0033975Next, we store the values using rbind
We can take a peak:
## t x y
## xy_t 0 0.010000 0.0010000
## xy 1 0.010445 0.0033975We can iterate over many time steps, each time storing the values:
# Iterate to compute the values as they change over time
for(t in 2:40){
xy = ross_diffs_1(xy, ross_dts_par)
xy_t = rbind(xy_t, xy)
} We can look at the last few values, the values of \(t,\) \(x\) and \(y\) are stored in columns:
## t x y
## xy 38 0.9857389 0.7104755
## xy 39 0.9858763 0.7107768
## xy 40 0.9859663 0.7109837As we can see, the values are changing a little at the end.
Notice that after 40 days, the values of \(x\) and \(y\) appear to be approaching some value asymptotically. This is an important feature of these systems, one that we would like to understand and explore a bit more in the following sections.
The discrete time model ross_diffs_1 can be implemented in a spreadsheet. We did one as a Google Sheet.
2.2.3 Analysis
2.2.3.1 Steady States
The fact that our variables asymptotically approach some values over time is an important feature of dynamical systems, so we would like to do some analysis to understand it better. If we look at Eq. (2.4), we can understand why. In this model, there is no change when the proportion of humans becoming infected is equal to the proportion clearing infections; and the proportion of mosquitoes becoming infected is equal to the proportion dying.
In the following, we compute how much the system is changing over time. We can simply iterate once and compare the differences. After iterating 40 times, the differences are very small:
# The last value is still stored as xy; the [-1] omits t
xy[-1] - ross_diffs_1(xy, ross_dts_par)[-1]## x y
## -5.903348e-05 -1.417083e-04If we iterate another hundred days and check again, the differences have gotten even smaller:
for(i in 41:140){
xy = ross_diffs_1(xy, ross_dts_par)
xy_t = rbind(xy_t, xy)
}
xy[-1] - ross_diffs_1(xy, ross_dts_par)[-1]## x y
## 0 0After simulating, the variables reach a steady state, where asymptotically \(x_{t+1} = x_t\) and \(y_{t+1} = y_t\).
A steady state occurs when there is no daily change, so \(x_{t+1} - x_t = 0\) and \(y_{t+1} - y_t = 0.\) We can figure out the steady state values are by substituting \(x_{t+1} = x_t = x\) and \(y_{t+1} = y_t = y\) into Eq.(2.4) and then solving for \(x\) and \(y\). After cancelling and rearranging, we get:
\[\begin{equation} \begin{array}{rl} m a y (1-x) &= s x \\ a x (1 - y) &= u y\\ \end{array} \tag{2.5} \end{equation}\]
Equations (2.5) say: the proportion of humans becoming infected is equal to the proportion clearing infections; and the proportion of mosquitoes becoming infected is equal to the proportion dying.
The most obvious solution to these equations is \(x=y=0,\) when there is no malaria. We call it the disease-free steady state. A disease-free equilibrium makes sense, since if we start with no infected mosquitoes or infected humans in this deterministic model, there can never be any.
There is another solution where malaria is present. We solve the second equation first:
\[y = a x / (u + a x).\]
Next, we substitute this for the \(y\) term that is in the first equation, and we get:
\[m a^2 (1-x) = s (u+ax)\]
and now we solve for \(x\)
\[x = \frac{\textstyle{ma^2 - su}}{\textstyle{ma^2 + sa}}\] We can write a function to compute this steady state:
# INPUTS
# params - the parameters, as a list
#
# OUTPUTS
# the steady state values of x and y
ross_dts_steady_0 = function(params){with(params,{
xx = (m*a^2 - s*u)/ (m*a^2 + s*a)
yy = a*xx/(u+a*xx)
c(x=xx,y=yy)
})}## x y
## 0.9861386 0.71142862.2.3.2 Thresholds
All our analysis worked out well for the parameter values that we chose, but what if we had picked different parameters?
There must be some very low level of mosquitoes, for example, where malaria parasites can’t be sustained in a population. If we reduce \(m\) to \(0.005\) and evaluate the expression at the steady state, we get negative values for \(x\) and \(y\).
## x y
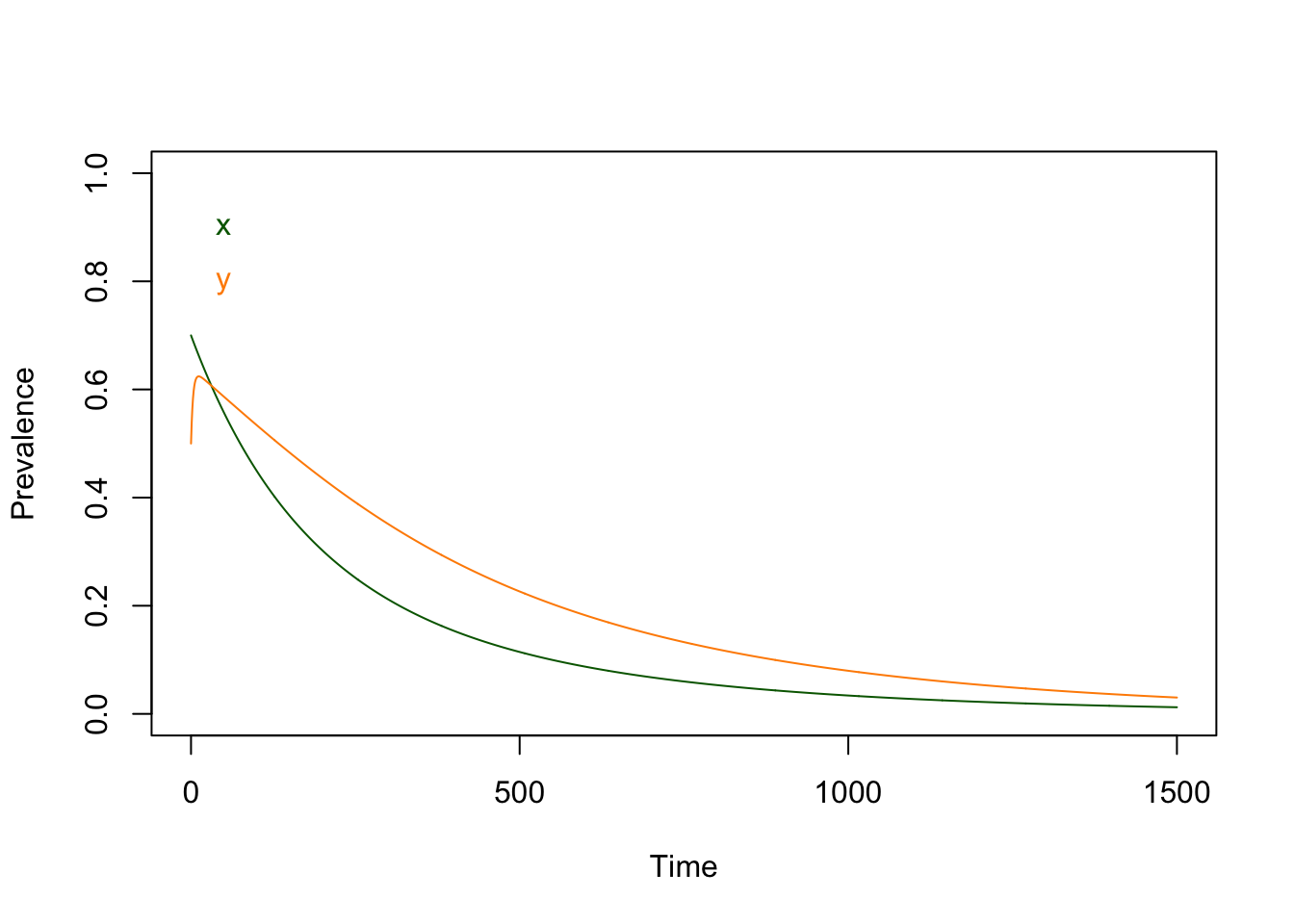
## -0.1200000 -0.4285714What happens if we simulate this? (Let’s set the initial conditions to reasonably high values)
# Set initial conditions
xy = c(t=0, x=0.7, y=0.5)
xy_t = xy
# Solve
for(t in 1:1500){
xy = ross_diffs_1(xy, ross_dts_par1)
xy_t = rbind(xy_t, xy)
}
# Plot
with(as.data.frame(xy_t), {
plot(t, x, "n", ylim = range(0, 1), ylab = "Prevalence", xlab = "Time")
lines(t, x, col = "darkgreen", pch =15)
lines(t, y, col = "darkorange", pch =19)
text(10, 0.9, "x", col = "darkgreen", pos=4)
text(10, 0.8, "y", col = "darkorange", pos=4)
})
Our function ross_dts_steady_0 gives us a negative number.
## x y
## -0.1200000 -0.4285714If we look at the equations, it’s easy enough to spot the problem. Since \(x\) and \(y\) must be positive, then it must be true that \[m a^2 > su.\] We call this a threshold condition.
## [1] 0.008If we check, we find that this gives us the disease free equilibrium.
## x y
## 0 0It doesn’t make sense to have a negative amount of malaria. Since ross_dts_steady_0gives us negative numbers, we can use this little bit of information to write a better function, one that returns \(0\) instead of a negative number:
# INPUTS
# params - the parameters, as a list
#
# OUTPUTS
# the steady state values of x and y
ross_dts_steady_1 = function(params){with(params,{
xx = ifelse(m*a^2 > s*u, (m*a^2 - s*u)/(m*a^2 + s*a), 0)
yy = a*xx/(u+a*xx)
c(x=xx,y=yy)
})}## x y
## 0 0In The Ross-Macdonald Model, we’ll take another look at thresholds.