10.3 Stable Orbits

If emergence rates vary seasonally, how much of the analysis that we did to understand steady states still holds? Obviously, if conditions are changing seasonally, the model does not reach a steady state. In fact, after modification to suit the context, many of the same principles translate. The steady state analysis provides a good qualitative guide, but that the answers will look different. Here, we illustrate by solving systems to illustrate some basic points, which is easy enough. Analysis of the resulting dynamics can be quite difficult; it is covered in Temporal Dynamics.

10.3.1 Thresholds

There is a threshold condition $R_0>1$ that determines whether malaria is endemic, but the formula for $R_0$ depends on the form of $\Lambda(t)$. If we set $R_0=1$, we can show that the threshold for persistence in a seasonal environment is $R_0 > \sigma > 1$ (see Figure 1.1). The math to compute threshold conditions in seasonal environments is in Temporal Dynamics.

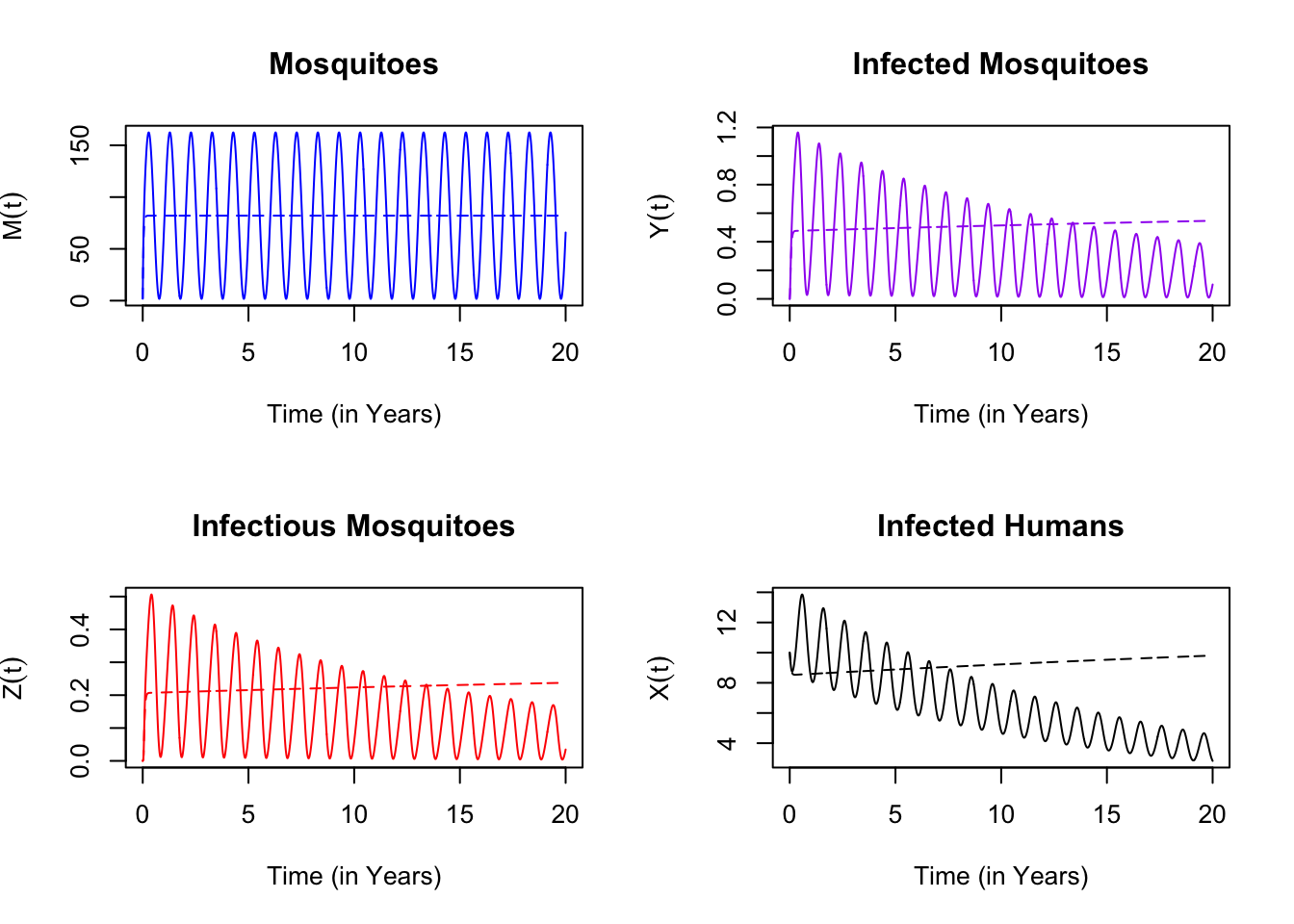
Here, we set $R_0= 1.02$ for the model with constant emergence, and we show that malaria persists. For the same parameters and for the same *average* emergence rate, malaria declines with seasonality.

Figure 10.2: Here, we set $R_0= 1.02$ for the model with constant emergence, and we show that malaria persists. For the same parameters and for the same average emergence rate, malaria declines with seasonality.

10.3.2 Orbits

If $R_0 >1$, then all orbits converge to a set of stable orbits (See Figure 1.1). If $\Lambda(t)$ has an annual cycle, then after the orbits converge:

- $M(t+365) = M(t)$; 
- $Y(t+365) = Y(t)$ and $Z(t+365) = Z(t)$; 
- $X(t+365) = X(t)$.

Figure 10.3: With different initial values, the orbits converge and eventually lie on top of one another.

10.3.3 Average Dynamics

If $R_0>1$ and malaria is endemic, the average prevalence of malaria infection is variable in a seasonal environment. While the prevalence is higher at the peak, the average for the whole year tends to be lower.

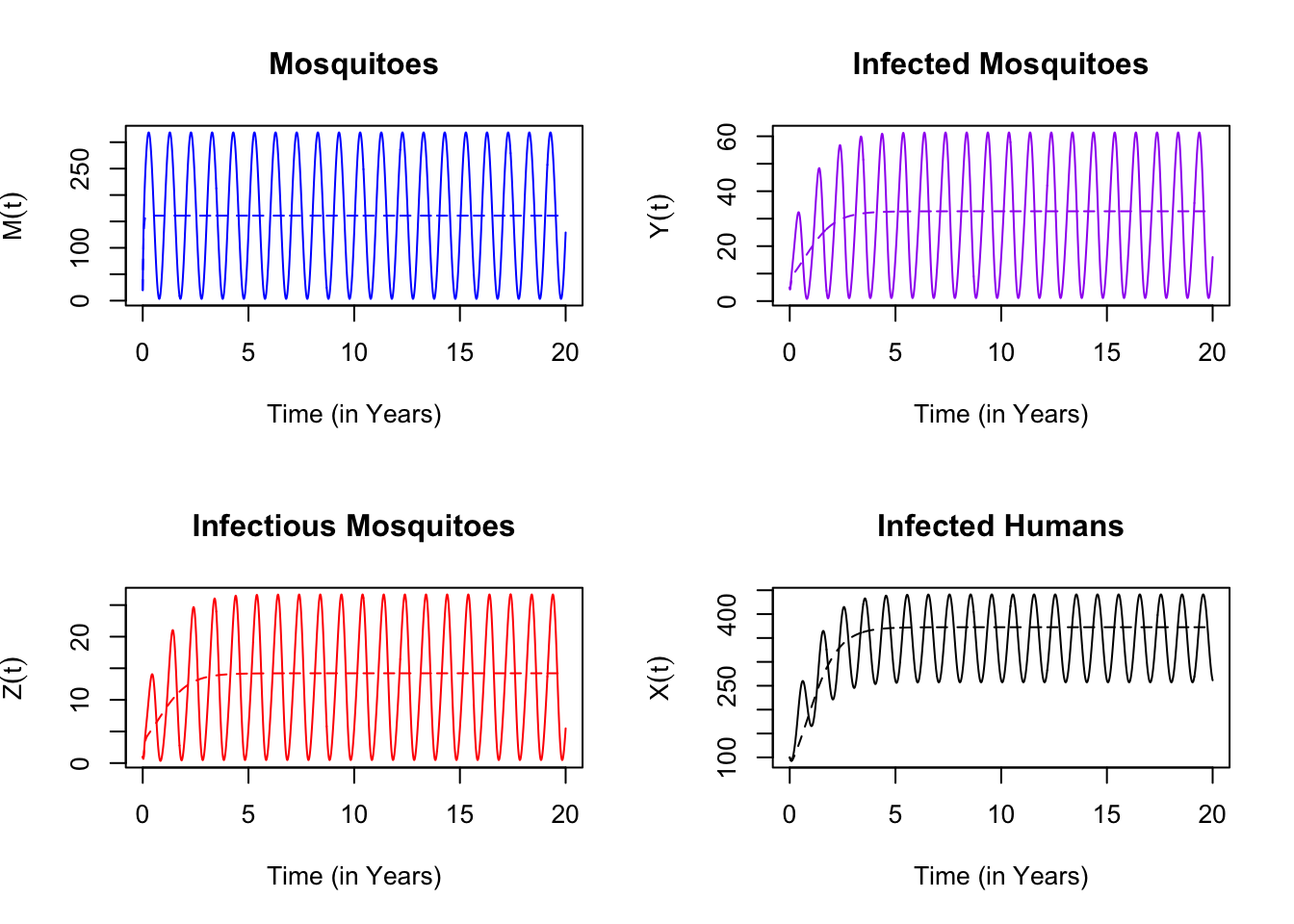
Here, we set $R_0= 2$ for the model with constant emergence, and we show that the prevalence of malaria is similar in the seasonal environment, but it's higher as transmission peaks, lower in the off-season, and lower overall.

Figure 10.4: Here, we set $R_0= 2$ for the model with constant emergence, and we show that the prevalence of malaria is similar in the seasonal environment, but it’s higher as transmission peaks, lower in the off-season, and lower overall.