2.1 Ross’s Quantiative Logic
As Ross was planning malaria control activities, he sought to develop mathematics for support malaria control planning. He was looking for a way of setting rational expectations about the likely outcomes of control. Given his interests in malaria metrics, he sought to understand why malaria prevalence differed from place to place. To explain these differences, he developed mathematical models that described the processes affecting how malaria prevalence would change over time: infection and the loss of infection.
To develop a mathematical model, Ross believed that it was possible to write down a priori – or in other words, to formulate mathematical models using quantitative logic – a description of the process. Malaria infections in two host populations – humans and mosquitoes – are connected through mosquito blood feeding, so malaria transmission works as an integrated system with two otherwise independent compoonents. The process looks something like the following diagram.
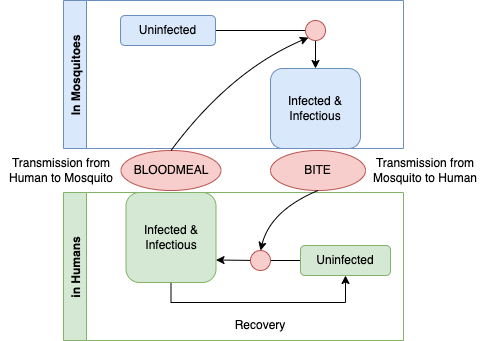
This graph is the basis for causal theory for understanding malaria parasites in populations. A student of causation might object that the graph describes a cycle and thus it can not be causal. If we applied the logic more generally, no graph describing any organisms life cycle would be causal, and yet life is undoubtedly the cause of life. The missing element is time: a life-cycle graph would be directed and acyclic if it had an arrow that traced life in one generation giving rise to life in the next. To understand this as a causal diagram, we must thus imagine that it describes a dynamical process in populations: infected mosquitoes today are biting and infecting humans tomorrow; and infectious humans today are causing infections in mosquitoes tomorrow when they take a blood meal. Seen in this way, we can begin to develop a quantitative theory that describes all the factors that determines malaria prevalence in populations. How does malaria persist in a population? It persists through the transmission of parasites among hosts during blood feeding. What factors determine prevalence? It is a balance between the gain and loss of infection.
To write down the model, we must make some assumptions about the process. We begin with an abstract concept of place – here. We imagine that populations here are comprised of individual mosquitoes and individual humans, and we are interested in computing the fractions of humans and mosquitoes that are infected. Since infections don’t last forever, the prevalence of infection in mosquitoes and humans reflects a balance between infections acquired through parasite transmission and the natural loss of infection through parasite clearance or host mortality. In many places, forces affecting the the balance can be changing; mosquito population density fluctuates over time, for example. Ross’s equations assumed that transmission by mosquitoes was constant over time, and they focused on local transmission, ignoring exposure elsewhere (e.g. through travel). This model thus ignores many factors that would be important for planning for control. Ross discussed all these factors, but since he was pioneering a new approach, the models were very simple.
Mosquitoes lived short lives, so the loss of parasites in mosquitoes would mainly occur through mosquito mortality:
\[\begin{equation} \mbox{MOSQUITOES} \\ \; \\ \left[ \begin{array}{rcl} \mbox{Infected Tomorrow} &=& \mbox{Infected Today} \\ &-&\mbox{Infected: Died}\\ &+&\mbox{Uninfected: Got Infected}\\ \end{array} \right] \tag{2.1} \end{equation}\]
This description of a process ignores the loss of infection in mosquitoes, and changing mosquito population density. It ignores the extrinsic incubation period (EIP), the lag between the point in time when a mosquito gets infected and when it becomes infectious. This basic description of the process does not explicitly address the process that gives rise to uninfected mosquitoes. The mathematical formulation implies, without stating it explicitly, that each dying infected mosquito gets replaced by an uninfected mosquito emerging from an aquatic habitat. Otherwise, the mosquito population would declining over time. Ross was interested in malaria transmission dynamics, so the mosquito ecology was almost invisible.
Humans live long lives, so parasite loss would mainly occur through natural clearance.
\[\begin{equation} \mbox{HUMANS} \\ \; \\ \left[ \begin{array}{rcl} \mbox{Infected Tomorrow} &=& \mbox{Infected Today} \;\; \\ &-& \mbox{Infected: Cleared Infection}\\ &+& \mbox{Uninfected: Got Infected}\\ \end{array} \right] \tag{2.2} \end{equation}\]
This description of the process thus ignores human demography, including births, deaths, and migration. The model also ignores a large number of other factors, including superinfection, the complex time course of an infection, immunity, and treatment with anti-malarial drugs. (In Ross’s day, quinine was expensive and difficult to obtain, but it was sometimes used.)
To describe malaria transmission and factors that determine the prevalence of malaria in human populations over time, we formulate mathematical models as dynamical systems. In the sections that follow, we will formulate dynamical systems in discrete and continuous time, and as a deterministic or stochastic processes.
As a reminder, we’re not trying to delve too deeply into malaria epidemiology with the models in this chapter. We’re trying to develop a toolbox that we can use to investigate malaria transmission dynamics and control.