2.7 Stochastic, Continuous Time

In continuous time, the state of the system is updated one event at a time.

• The total rate of change of the system is \(T = may(H-X) + rX + aX(M-Y) + gY\)

• \(Y \rightarrow Y+1\)

• \(Y \rightarrow Y-1\)

• \(X \rightarrow X+1\)

• \(X \rightarrow X-1\)

# The parameters, as list 
ross_sxde_par = list(
  r = 1/200, # The clearance rate for infections 
  g = 1/12,  # The mosquito daily death rate 
  a = 1/4,   # The mosquito human blood feeding rate 
  M = 50,   # The number of mosquitoes 
  H = 100    # The number of humans
) 

ross_sxde = function(XY, pars){
  with(as.list(XY), with(pars,{
    p1 = a*Y*(H-X)/H
    p2 = r*X 
    p3 = a*X*(M-Y)/H
    p4 = g*Y 

    t = t + rexp(1, p1+p2+p3+p4)
    
    event = sample(1:4, 1, prob=c(p1, p2, p3, p4))
    if (event==1) X <- X+1
    if (event==2) X <- X-1
    if (event==3) Y <- Y+1
    if (event==4) Y <- Y-1
    
    return(c(t=t,  X=X, Y=Y, x=X/H, y=Y/M))
}))}

xy = c(t=0, X=10, Y=10)
for (i in 1:5){
  xy <- ross_sxde(xy, ross_sxde_par)
  print(xy)
}

##           t           X           Y           x           y 
##  0.05978781 11.00000000 10.00000000  0.11000000  0.20000000 
##          t          X          Y          x          y 
##  0.1714032 11.0000000  9.0000000  0.1100000  0.1800000 
##          t          X          Y          x          y 
##  0.5413876 11.0000000 10.0000000  0.1100000  0.2000000 
##         t         X         Y         x         y 
##  0.859444 12.000000 10.000000  0.120000  0.200000 
##         t         X         Y         x         y 
##  1.191776 13.000000 10.000000  0.130000  0.200000

sim_ross_sxde = function(pars, X0=2, Y0=1, tmax=300){
   XY = c(t=0, X=X0, Y=Y0) 
   tm = XY[1]
   XY_t = c()  
   while(tm < tmax){
     XY = ross_sxde(XY, pars)
     tm = XY[1]
     XY_t = rbind(XY_t, XY)
   }
   return(list(time=XY_t[,1], X=XY_t[,2], Y=XY_t[,3], x = XY_t[,4], y = XY_t[,5])) 
}

out <- sim_ross_sxde(ross_sxde_par)

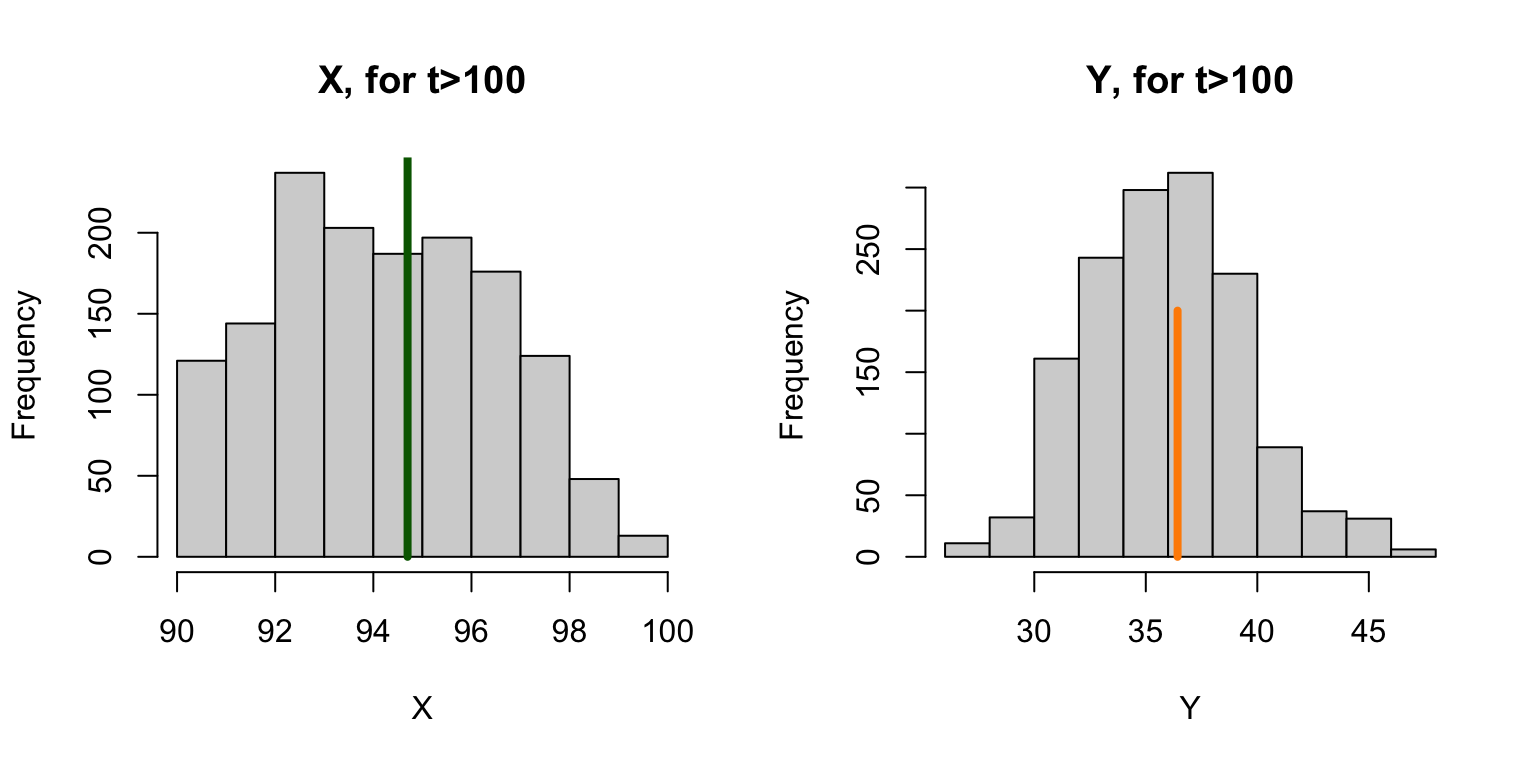
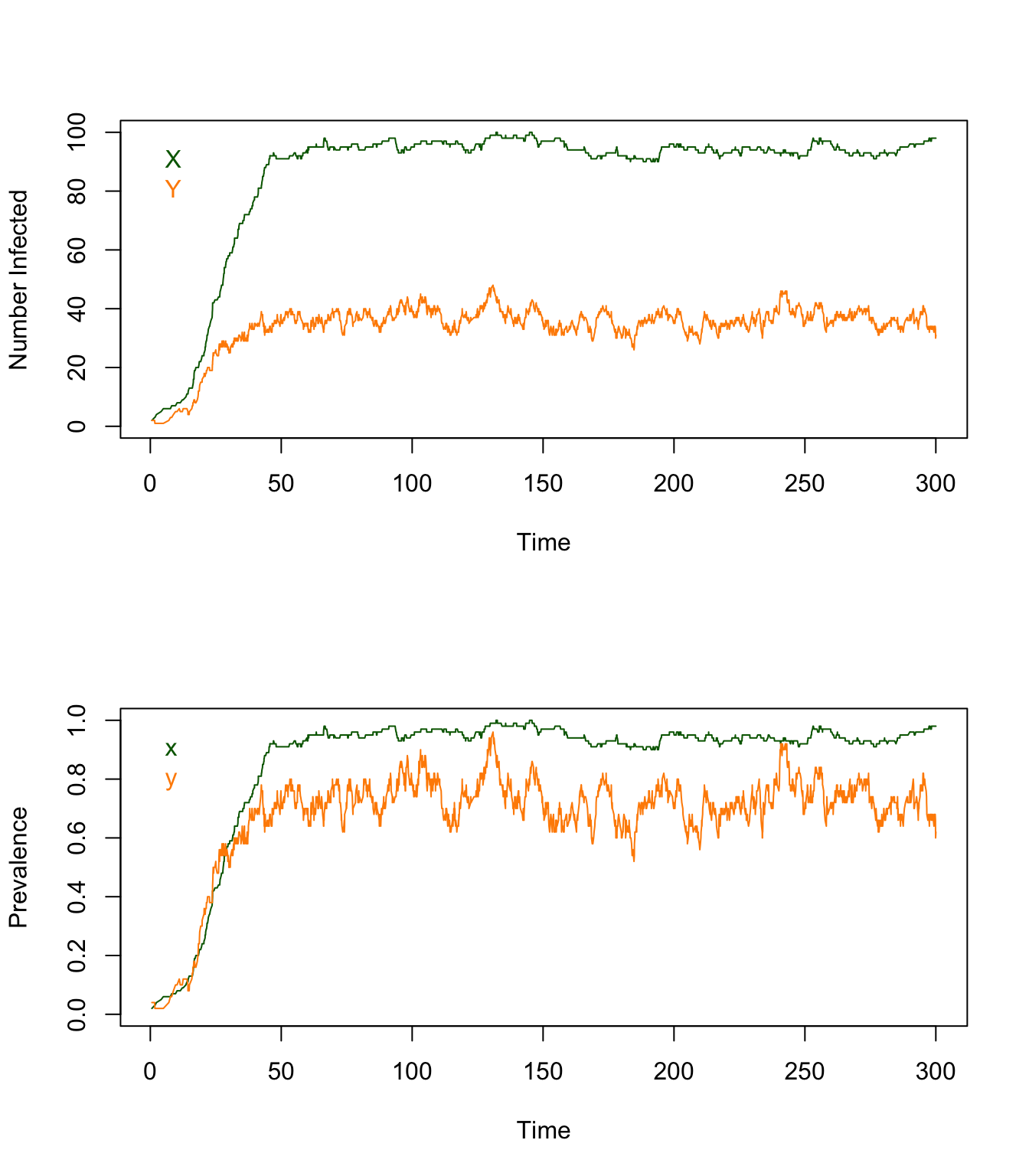
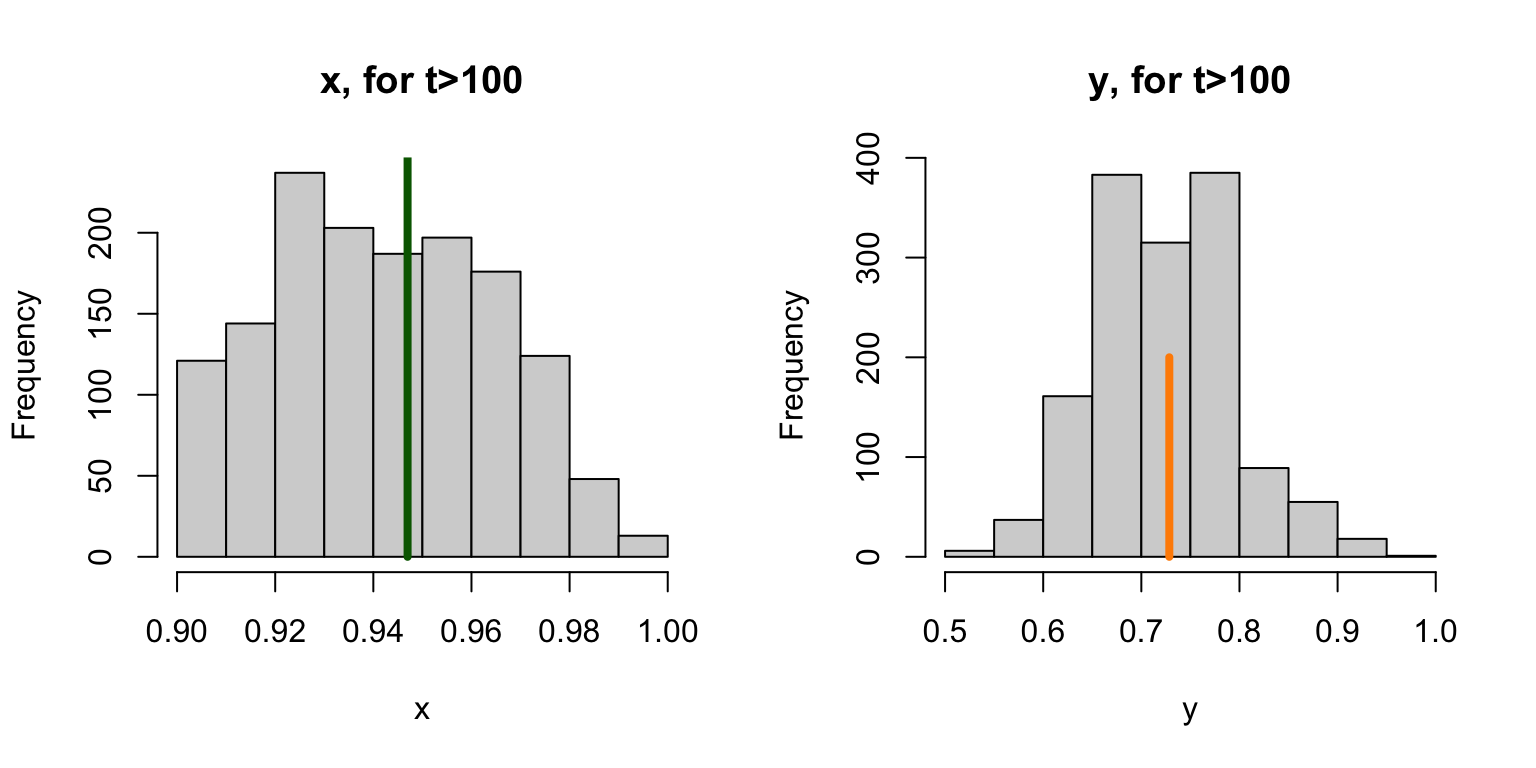
If we want to compare it to the other model, we can compute prevalence: