Evaluation

Routine Evaluation of Vector Control

library(ramp.xds)
library(Matrix)
library(expm)
library(ramp.library)
library(ramp.control)
library(ramp.work)

devtools::load_all("~/git/ramp.control")

ℹ Loading ramp.control

devtools::load_all("~/git/ramp.work")

ℹ Loading ramp.work

Routine evaluation of vector control for malaria presents enormous challenges. This vignette considers the challenge of evaluating the impact of mass bed net distributions and mass indoor house spraying (i.e. indoor residual spraying, or IRS).

To evaluate vector control, we need to do the following tasks:

Build a model
Set up model fitting
Set up vector control
Fit the model to data
Construct a counterfactual baseline
Compute the impact

Build a Model

We want to understand malaria as a changing baseline that has been modified by vector control. The malaria baseline is affected by mosquito ecology. To get started, we build a model to understand malaria prevalence in relation to exposure. We set up a model that is forced by the EIR:

sip <- xds_setup_eir(Xname = "SIP")

Set Up Fitting

The functions that set up model fitting in ramp.work use xds_scaling to make some initial guesses about the mean forcing parameters and the seasonal phase.

sip <- xds_scaling(sip)
xds_plot_eirpr(sip)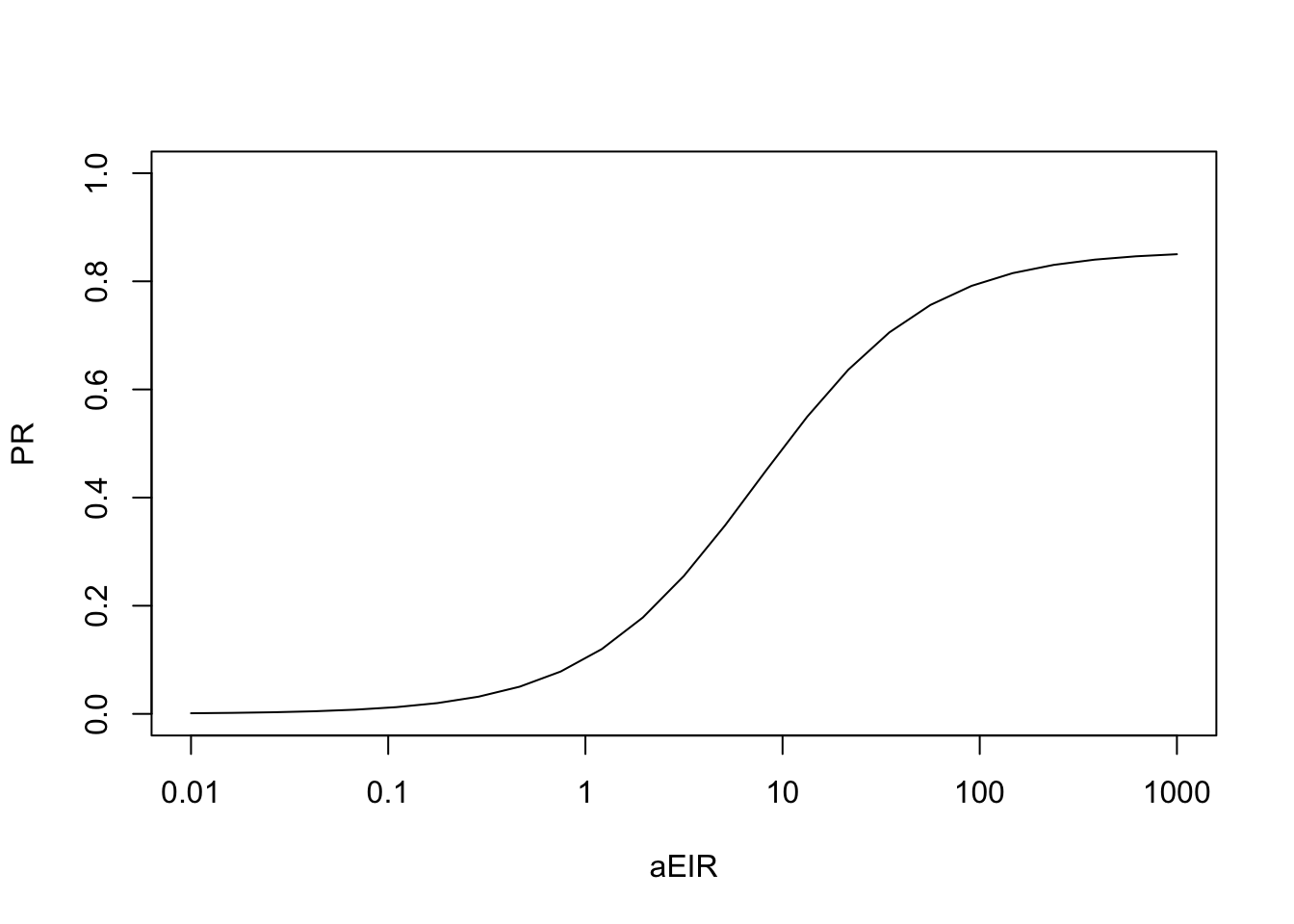

After fitting the model and getting the seasonal pattern right, it might be worth it to run xds_scaling again.

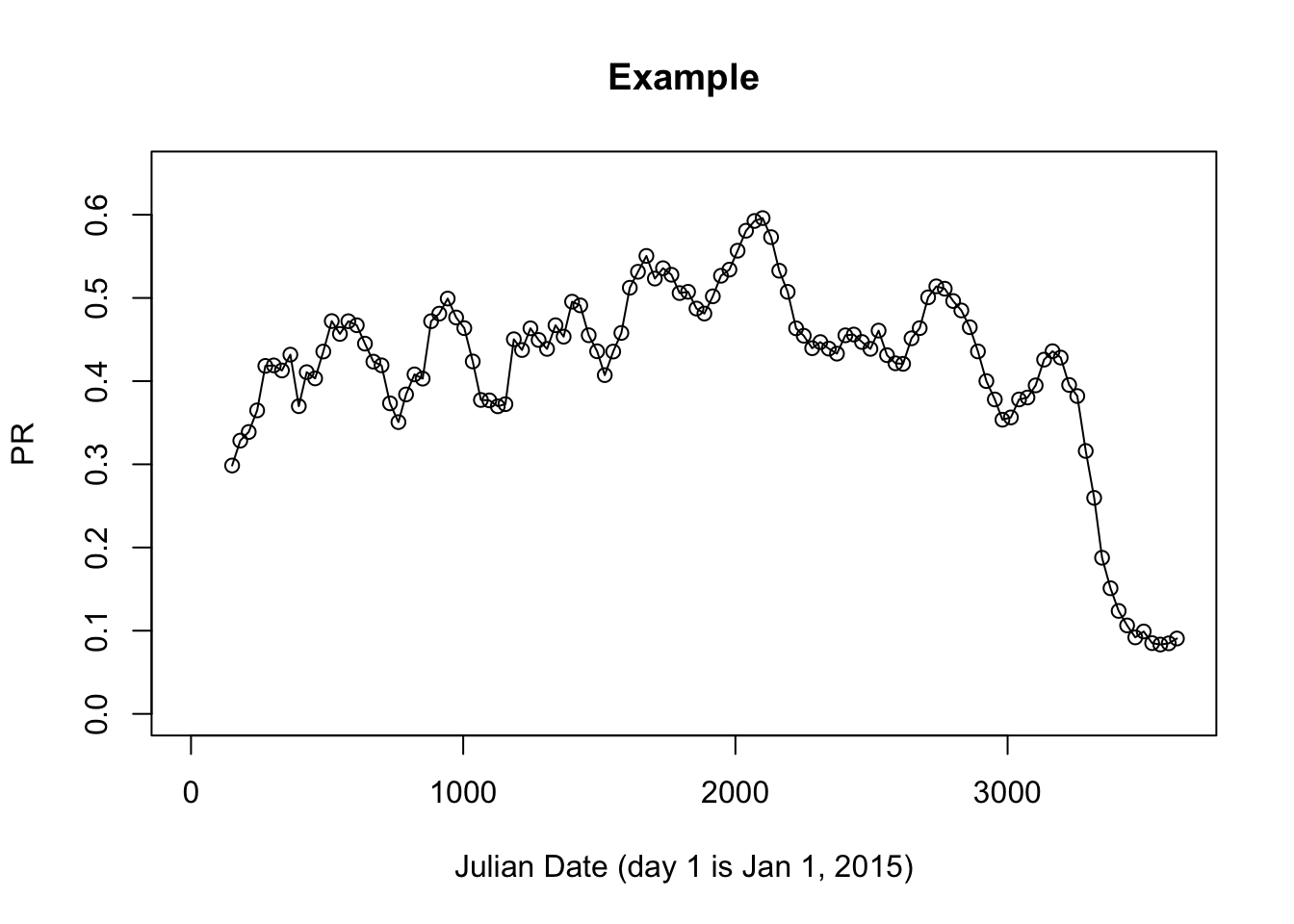
To set up model fitting, we need some data. We use a time series we have saved locally:

prts <- read.table("./data/pfpr_time_series.tbl")
with(prts, {
  plot(jdates, pfpr, ylim = c(0,0.65), main = "Example", xlab = "Julian Date (day 1 is Jan 1, 2015)", ylab = "PR", xlim = range(0, jdates)) 
  lines(jdates, pfpr)
})

sip <- setup_fitting(sip, prts$pfpr, prts$jdate)

Set Up Vector Control Events

To set up vector control for IRS, we use setup_irs_events and pass it the Julian dates, the pesticides, and the coverage (% of houses sprayed).

irs_jdates <- c(2861, 3256, 3622) 
irs_type <- c("fludora_fusion", "actellic", "actellic") 
frac_sprayed <- c(.95, .95, .95) 
sip <- setup_irs_events(sip, irs_jdates, irs_type, frac_sprayed)

To set up vector control for bed nets, we use setup_bednet_events and pass it the Julian dates, the net types, and peak access:

bednet_jdates <- c(-200, 776, 2176, 3240)
bednet_type <- rep("pbo", 4)
bednet_peak <- rep(0.95, 4)
sip <- setup_bednet_events(sip, bednet_jdates, bednet_type, bednet_peak)

Before we do any fitting, we want to take a look at the \(t\)-values of the interpolation points. The default spacing is once a year, but if we want to evaluate vector control, we might want values at sensible points before and after the mass distribution events. There’s a lot going on in the following:

The PfPR time series is a set of squares
The line shows the model with preliminary guesses
The vertical lines show the timing of mass distribution / spraying events:
- irs is in blue
- bednets is in red
- the # describes the round (there’s a bednet found before our data start)
- the text describes the round
the \(\oplus\) symbols show the original spline \(t\)-values
the purple squares are an alternative spacing for the \(t\)-values returned by event_chop_spline_t

show_fit(sip) 
show_events(sip, mx=0.4)
ti <- event_chop_spline_t(sip, fu=200, b4=20, mngp=120)
points(ti, 0*ti, pch = 15, col = "purple")

To set the stage for evaluating, we’ll shift the spacing of the time points to the purple squares.

sip <- fitting_replace_spline_t(ti, sip)

Fit the Model

Now we fit the model to the data.

sip <- pr2history_xm(sip)

show_fit(sip)
show_events(sip, mx=0.4)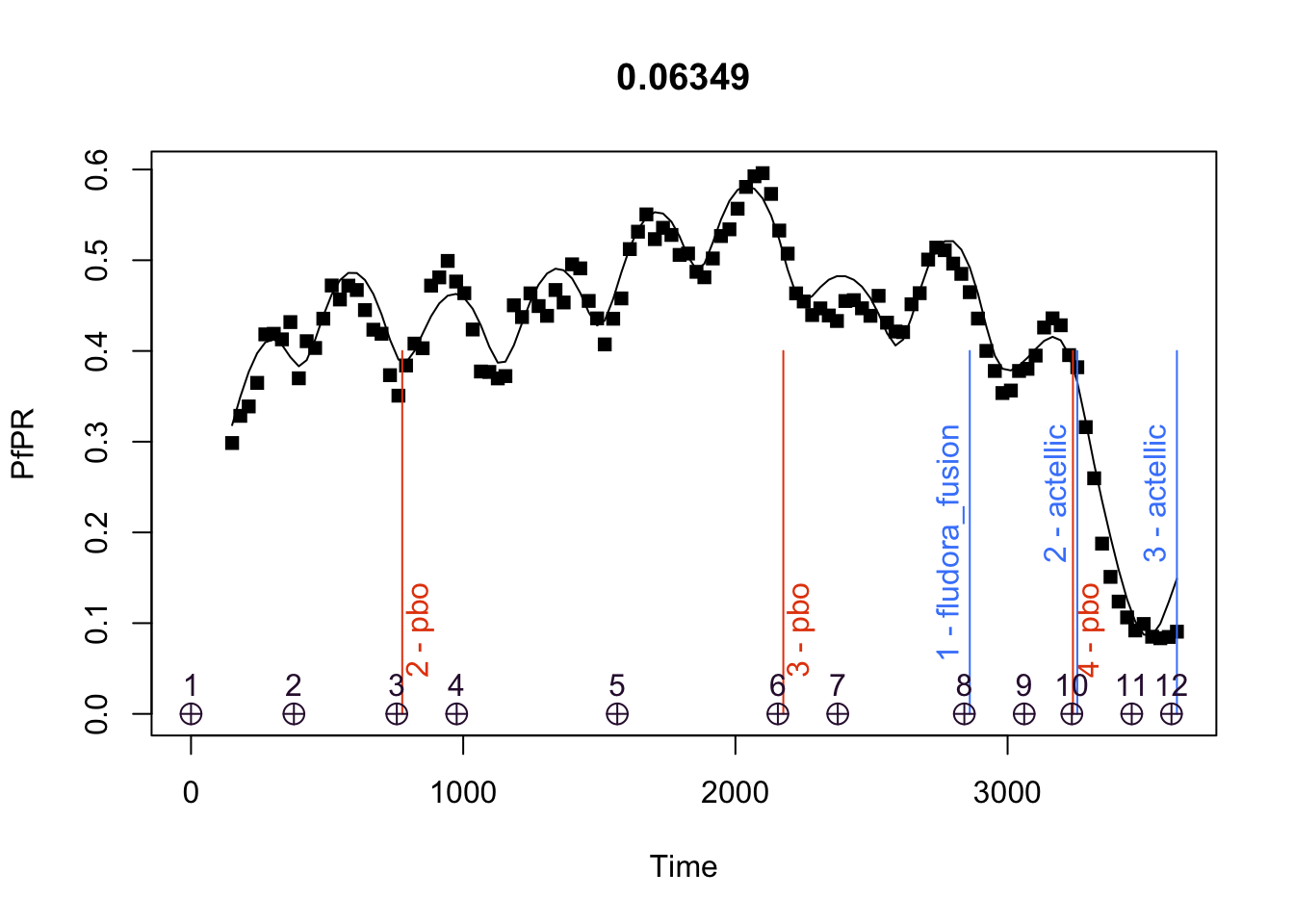

Counterfactual Baseline

To evaluate vector control, we have to grapple with the problem of understanding malaria transmission as a changing baseline that has been modified by control. The challenge for malaria is that every place is different, so we have to learn about each place. The information we have about malaria is limited. What would have happened in the absence of any control?

If all we have is a time series that describes a reality that has been modified by control, what information do we have about the unmodified baseline?

To construct a spline-based counterfactual, there are three steps:

Get information about the baseline
Impute new \(y\)-values for the spline interpolation points
Simulation the baseline

Information about the Baseline

Above, we used show_events to visualize the history of malaria and the model set up.

In this time series, we note the large gaps between mass distribution events. Perhaps we can use these gaps to make some good guesses about the baseline. We use a function time_since_event to get a measure of the number of days elapsed since the last event.

time_since_event(sip)

 [1]    0  578  956  200  790 1380  200  665  200  375  200  346

If we use the arbitrary cutoff of a year, we find a set of five values for the interpolation points that we trust.

which(time_since_event(sip)>365) -> my_ix
my_ix

[1]  2  3  5  6  8 10

We’re going to modify the object to model a counterfactual. Here, we create models to evaluate bed net rounds 2 and 3.

Impute

Having decided where to get information about the baseline, we need to use it to impute a new baseline value for the \(y\)-values that follow the mass vector control event.

For round 2, we want to impute a new value for the \(4^{th}\) interpolation point, the one that follows the 2nd round (set as impute_ix in the code block below).

get_yix_after_bednet_round(2, sip)

[1] 4

A somewhat arbitrary decision about what values to trust is to choose the ones that come just before the event, and one that comes just after (trusted_ix in the code block below). We pull the \(y\)-values and take their mean (set as new_y) in the block below).

Finally, we impute it (we replace it with new_y)

impute_ix = c(4)
trusted_ix = c(2,3,5)
fitting_get_spline_ty(sip)$yy[trusted_ix] -> trusted_y
new_y = mean(trusted_y)
fitting_change_spline_y(new_y, impute_ix, sip) -> sip1

There is a function that automates this:

sip1a <- impute_spline_y(impute_ix, trusted_ix, sip1, "mean")

The last argument is an option:

“mean” is the default
Other options are “median,” “min,” “max,” “first,” & “last”
An option called “subsamp” subsamples the variates
An option called “gam” fits a gamma distribution and returns random variates

Compute Impact

last_day <- max(prts$jdates)
first_day <- min(prts$jdates)
tm <- c(first_day:last_day)
sip <- xds_solve(sip, times = tm)

sip1 <- xds_solve(sip1, times = tm)
xds_plot_PR(sip1, clrs="darkred")
xds_plot_PR(sip, clrs="darkblue", add = T)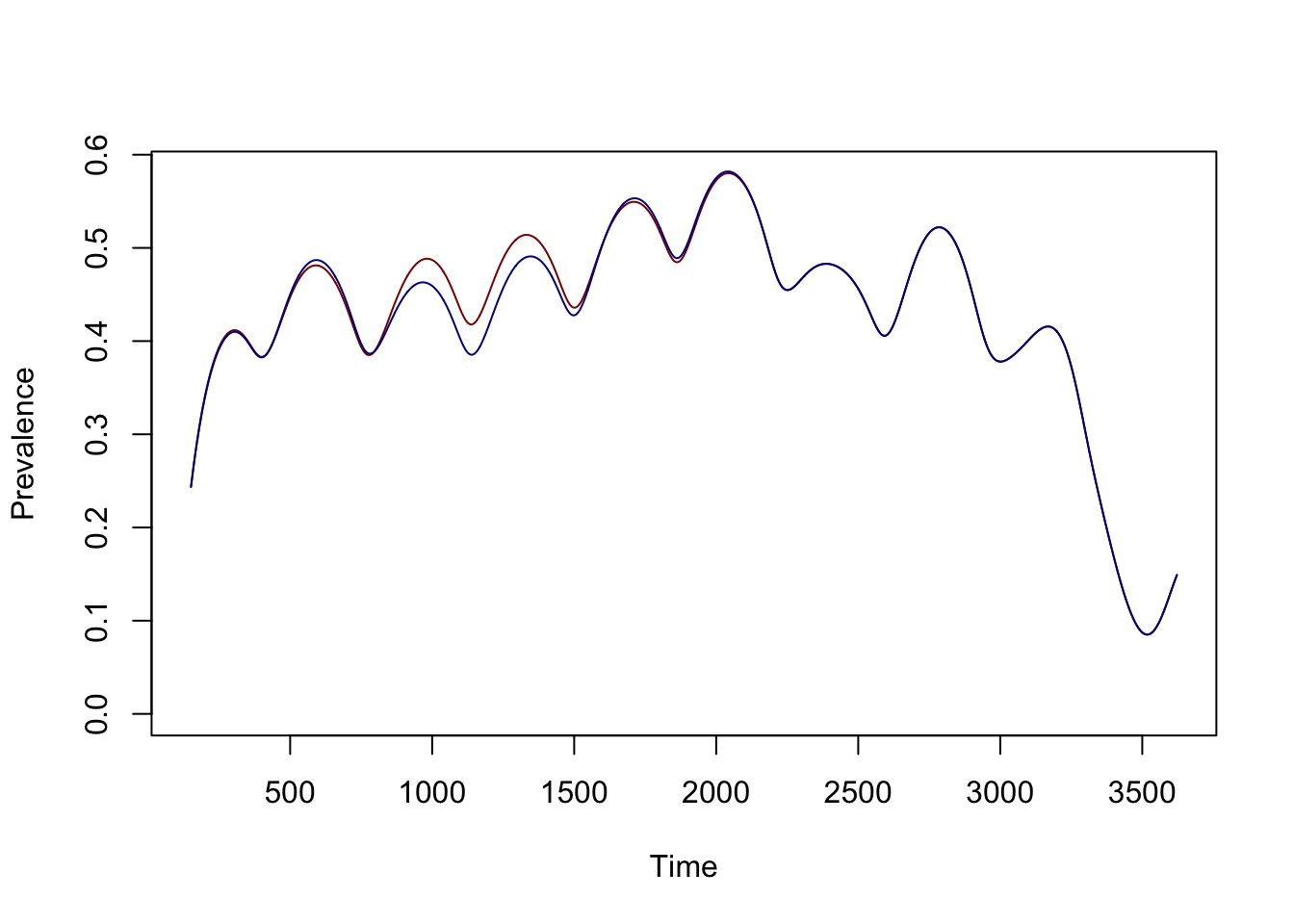

round_start <- sip$events_obj$bednet$jdate[2]
eval_period = round_start + 1:365
pr <- get_PR(sip)[eval_period]
pr1 <- get_PR(sip1)[eval_period]
impact = mean(pr1-pr)
plot(eval_period, pr1-pr, type = "l", ylab = "PR Difference", main = round(impact*1000)/1000)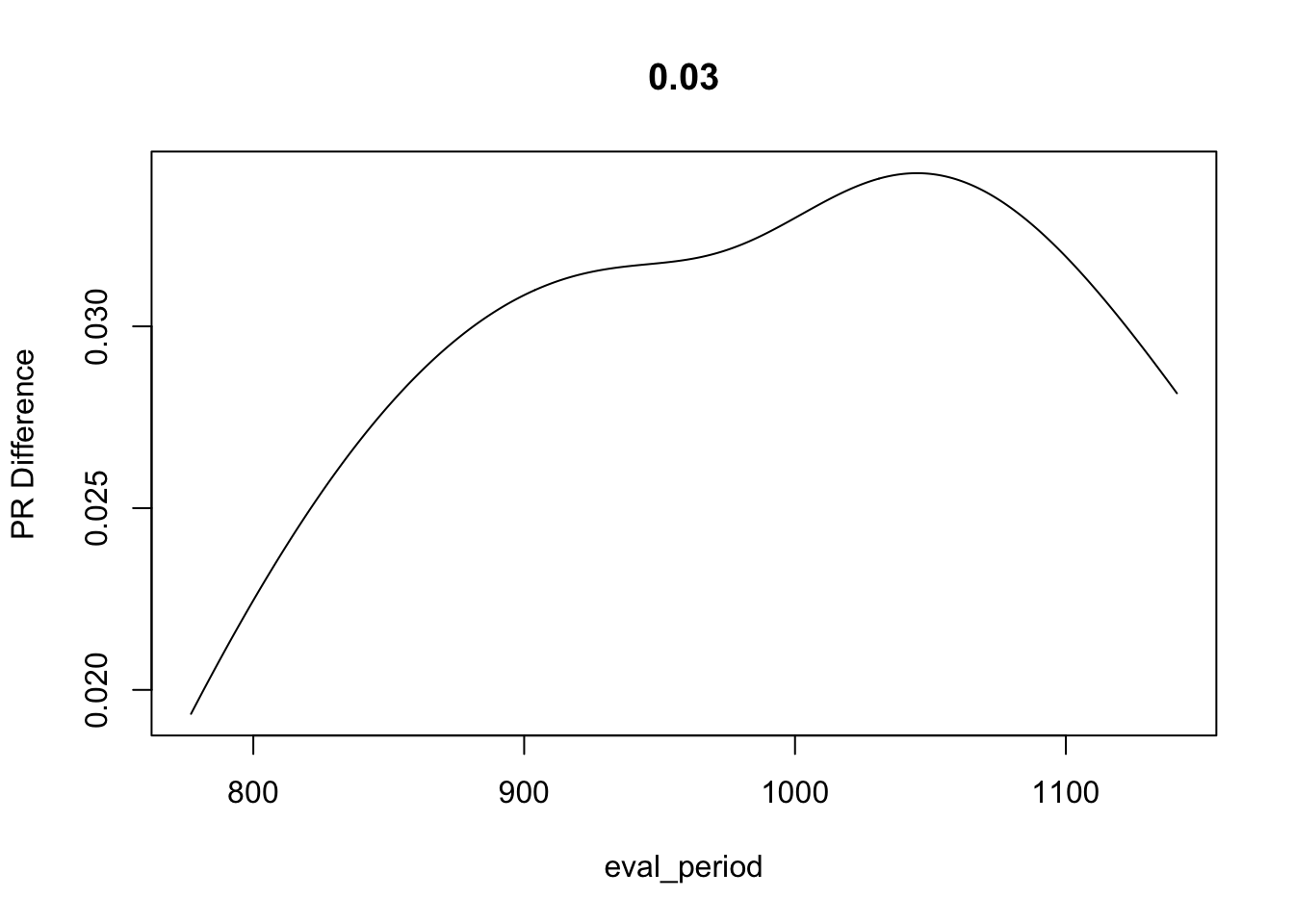

To make all this easier, we wrote a wrapper to compute measures of impact:

round_start <- sip$events_obj$bednet$jdate[2]
impact = compute_impact(sip, sip1, event_date=round_start)
names(impact)

[1] "pr_hist"       "pr_base"       "pr_averted_ts" "d_pr_max"     
[5] "d_pr_mean"     "t_eval"        "event_date"

with(impact, {
  plot(pr_base, type ="l", col = "darkred") 
  lines(pr_hist, col = "darkblue") 
 segments(event_date,0, event_date, max(pr_base))
})

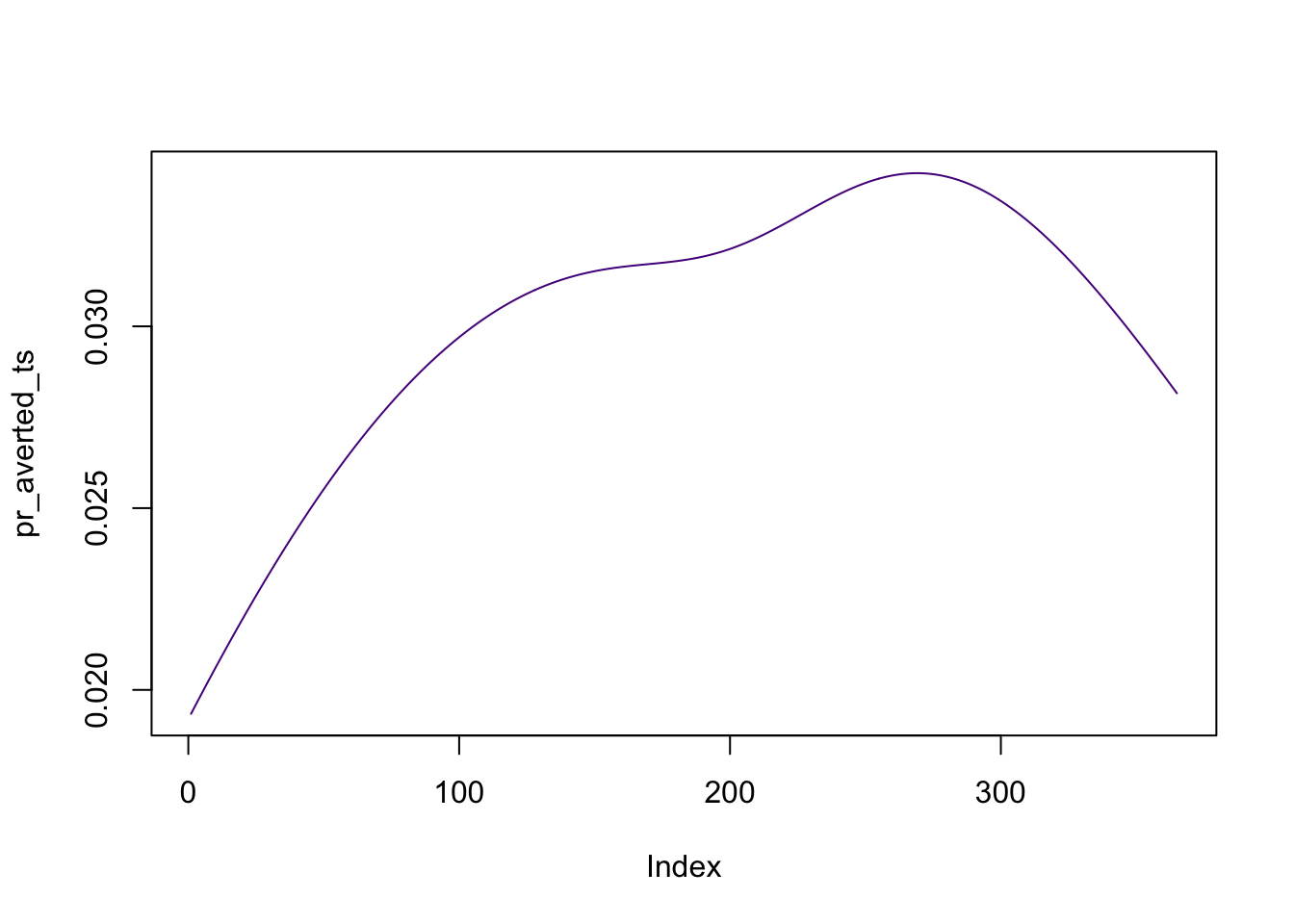
with(impact, {
  plot(pr_averted_ts, type ="l", col = "purple4") 
})

sip2 <- impute_spline_y(7, c(5,6), sip)
round_start <- sip$events_obj$bednet$jdate[3]
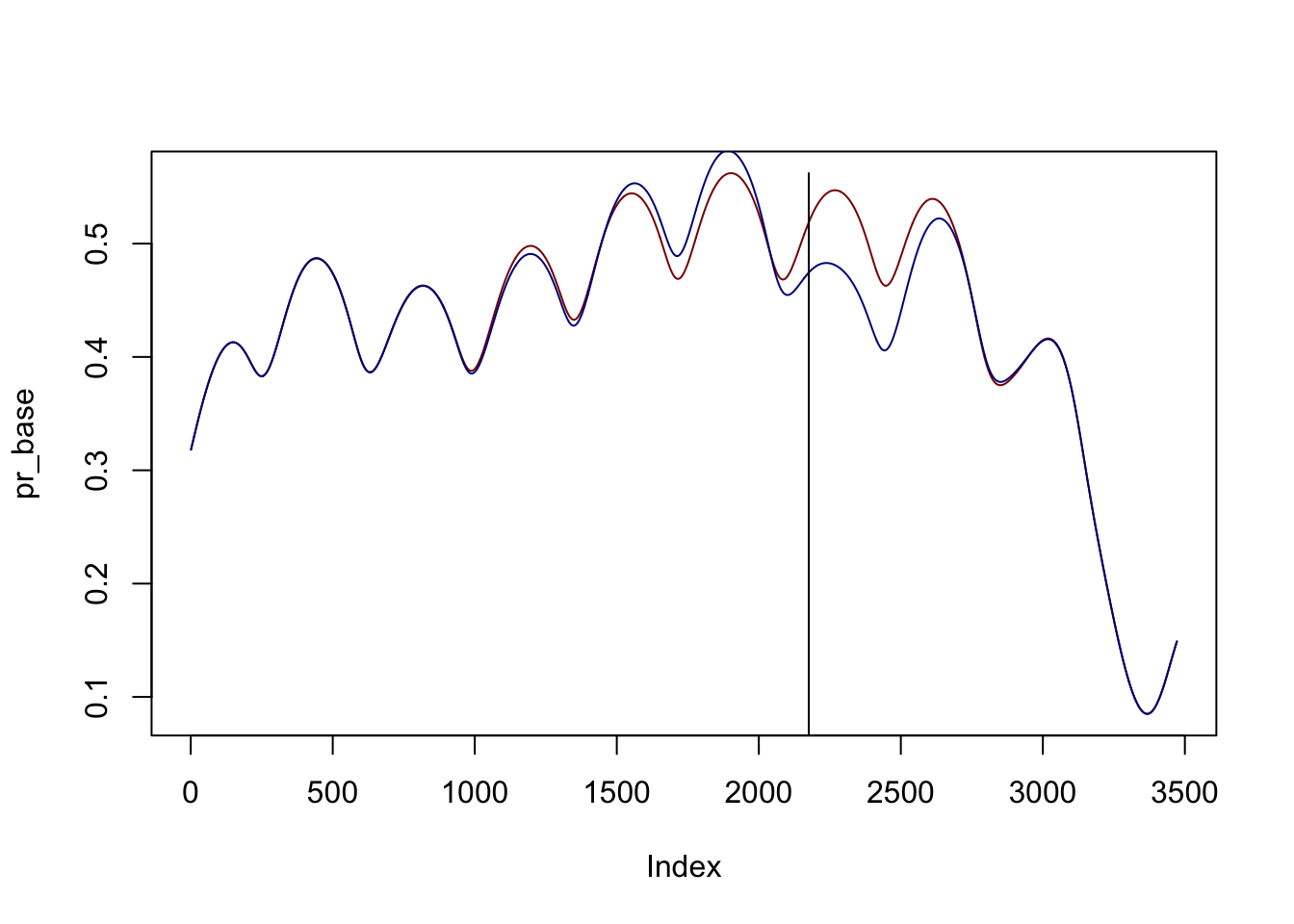
impact2 <- compute_impact(sip, sip2, event_date=round_start)

with(impact2, {
  plot(pr_base, type ="l", col = "darkred") 
  lines(pr_hist, col = "darkblue")
  segments(event_date,0, event_date, max(pr_base))
})

with(impact2, {
  plot(pr_averted_ts, type ="l", col = "purple4") 
})