Demo

Welcome

This assumes familiarity with R, dynamical systems & malaria.

To get started, install ramp.xds from the GitHub repository using devtools::install_github():

library(devtools)
devtools::install_github("dd-harp/ramp.xds")

Then load it:

library(ramp.xds)

A Model

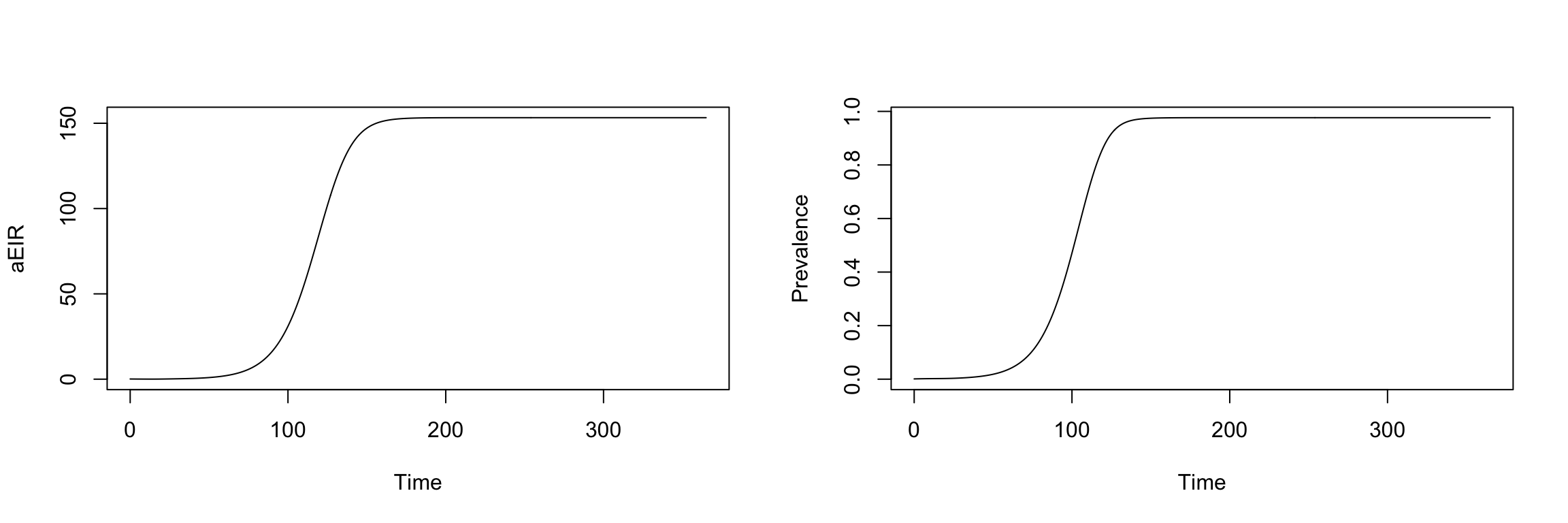
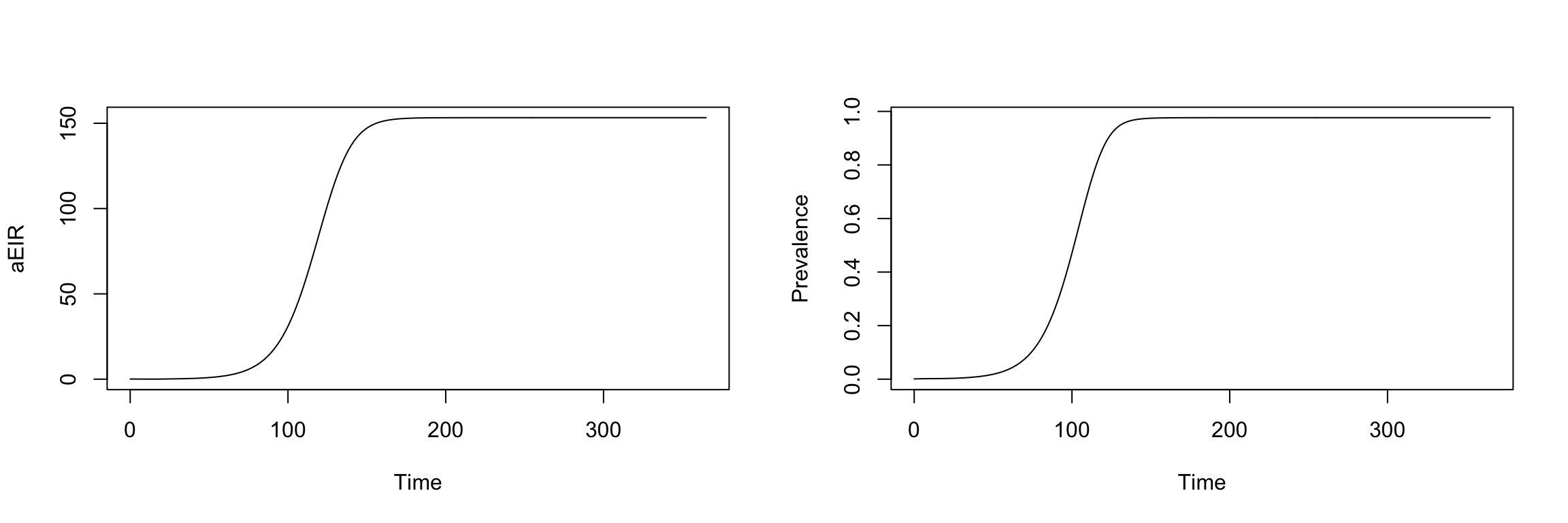
In ramp.xds, it’s easy to build, solve, and visualize malaria models, formulated as dynamical systems:

demo_mod <- xds_setup()
demo_mod <- xds_solve(demo_mod)
par(mfrow = c(1,2))
xds_plot_EIR(demo_mod)
xds_plot_PR(demo_mod)

The xds Object

The object that was returned by xds_setup(), that we named demo_mod, is a compound list called an xds object. Three text strings define the class of each dynamic module:

demo_mod$Xname

[1] "SIS"

demo_mod$MYZname

NULL

demo_mod$Lname

[1] "trivial"

Setup:: Defaults

xds_setup() supplies default values:

• default dynamic modules (i.e. SIS, macdonald, and trivial) recreate a model published in 1982 [1];

• each dynamic module sets up its own default parameters & initial values;

• all structural parameters are set to \(1\) (i.e., the number of patches, aquatic habitats, host strata, host species, & vector species)

In a few slides, we’ll describe how to change the defaults.

The xds Object : X module

The X component – a dynamical module describing infection dynamics & immunity in humans or other vertebrate hosts – is dispatched by Xpar[[i]]. Basic setup sets up only the first host species:

demo_mod$Xpar[[1]]

NULL

The xds Object : MYZ module

The MYZ component defines adult mosquito ecology and infection dynamics for each vector species, stored in MYZpar[[i]]:

class(demo_mod$MYZpar[[1]])

[1] "NULL"

The xds Object : L module

The L component defines aquatic mosquito population dynamics for each vector species, stored in Lpar[[i]]:

class(demo_mod$Lpar[[1]])

[1] "NULL"

The trivial module is a function that emergence rate of adult mosquitoes, \(\Lambda(t).\) Here, the scaling parameter is called Lambda

demo_mod$Lpar[[1]]$Lambda

NULL

’## Trivial modules & Forcing

To implement plug-and-play modularity, each component has a trivial module. All trivial modules return a function of time:

\[s \times F_S(t) \times F_T(t)\]

• \(s\) is a scale parameter named in context (e.g. Lambda)

• \(F_S(t)\) is the seasonal pattern, returned by F_season

• \(F_T(t)\) is an inter-annual trend, returned by F_trend

Some function families can be set up by make_function

Setup :: xds_setup

Setting up basic features is easy using xds_setup_*()

• xds_setup() can be used for most situations

• xds_setup_cohort() sets up a human / vertebrate host model forced by \(F_{E}(a,t),\) a function that returns the daily EIR as a function of age and time.

• Other xds_setup_*() functions streamline special cases and define a frame for solving, described in the documentation

Setup :: Dynamic Modules

• Dynamic modules are configured by passing:

  • Xname = "model_name"
  • MYZname = "model_name"
  • Lname = "model_name"

• The values in a named list overwrite default parameters & initial values:

  • Xopts = list(X=1, r=1/180)
    
  • MYZopts = list(M=1, g=1/5)
  • Lopts = list(L=1, psi = 1/5)

Setup :: Structural Elements

xds_setup() sets up a model with one host and one vector species:

• nPatches is the number of spatial units for adult mosquitoes

• membership indexes the patch membership of each habitat, passed as a vector where \(\mbox{max}(\)membership\()\leq\)nPatches and nHabitats\(=\mbox{length}(\)membership\()\)

• HPop is the population size of the strata, residence indexes the patches where the humans reside, and
  nStrata\(=\mbox{length}(\)HPop\()= \mbox{length}(\)residence\().\)

Setup :: Spatial Dynamics

Solving

It’s also easy to visualize the outputs:

par(mfrow = c(1,2))
xds_plot_EIR(demo_mod)
xds_plot_PR(demo_mod)

References

1.

Aron JL, May RM. The population dynamics of malaria. In: Anderson RM, editor. The Population Dynamics of Infectious Diseases: Theory and Applications. Boston, MA: Springer US; 1982. pp. 139–179. Available: https://doi.org/10.1007/978-1-4899-2901-3_5