Chapter 15 Regularization and Feature Selection

We assume you have loaded the following packages:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

Below we load more as we introduce more.

For replicability, we also set the seed:

np.random.seed(1)

15.1 How highly correlated features fail

df = pd.read_csv("../../../tyyq/teaching/data/toy/correlated-data.csv.bz2",
                 sep = "\t")
df.shape

## (100, 41)

df.columns

## Index(['y', 'x1', 'x2', 'x3', 'x4', 'x5', 'x6', 'x7', 'x8', 'x9', 'x10', 'x11',
##        'x12', 'x13', 'x14', 'x15', 'x16', 'x17', 'x18', 'x19', 'x20', 'z1',
##        'z2', 'z3', 'z4', 'z5', 'z6', 'z7', 'z8', 'z9', 'z10', 'z11', 'z12',
##        'z13', 'z14', 'z15', 'z16', 'z17', 'z18', 'z19', 'z20'],
##       dtype='object')

from sklearn.model_selection import train_test_split

y = df.y
X = df.drop("y", axis = 1)
X = pd.get_dummies(X, drop_first = True)
Xt, Xv, yt, yv = train_test_split(X, y, test_size = 0.4,
                                  random_state = 8)
Xt.shape

## (60, 60)

from sklearn.linear_model import LinearRegression

m = LinearRegression()
_t = m.fit(Xt, yt)
m.coef_  # look bad

## array([-2.45595396e+13,  2.45595396e+13, -4.37259242e+13,  4.37259242e+13,
##         2.89321620e+12, -5.78643241e+12, -3.54833759e+13,  3.54833759e+13,
##         2.89321620e+12, -2.78359375e+01, -3.90951458e+12,  3.90951458e+12,
##         4.37408111e+13, -4.37408111e+13,  1.69556095e+13, -1.69556095e+13,
##         3.42580122e+13, -3.42580122e+13,  1.15105671e+12, -1.15105671e+12,
##        -3.90314157e+11, -1.18694825e+11, -4.00119287e+11,  9.27898667e+09,
##        -4.90814409e+11, -1.94987306e+12, -3.31507912e+11, -9.56774076e+10,
##         3.12967608e+10,  1.56483804e+10,  1.94987306e+12,  1.45905865e+12,
##         7.19213769e+11,  2.28399359e+11, -3.31507912e+11, -9.56774076e+10,
##        -1.45905865e+12, -9.56774076e+10, -3.22044847e+11,  1.56483804e+10,
##        -1.56483804e+10, -9.56774076e+10, -3.31507912e+11, -9.56774076e+10,
##        -3.31507912e+11, -3.12967608e+10, -3.31507912e+11,  4.90814409e+11,
##        -3.31507912e+11, -9.56774076e+10, -3.31507912e+11, -9.56774076e+10,
##        -3.31507912e+11, -9.56774076e+10, -3.22044847e+11, -6.44089693e+11,
##         1.94987306e+12, -9.56774076e+10,  1.40185122e+12,  1.38620284e+12])

yhatt = m.predict(Xt)
rmset = np.sqrt(np.sum((yhatt - yt)**2))
rmset

## 5.446692317546288

m.score(Xt, yt)

## 0.9700622621554107

yhatv = m.predict(Xv)
rmsev = np.sqrt(np.sum((yhatv - yv)**2))
rmsev

## 2311619266721.474

m.score(Xv, yv)

## -1.0618673229473205e+22

Explore the case where highly correlated features fail. We create a small sample of random data where \(y\) is closely related to (true) \(x\). However, imagine we do not observe the true \(\boldsymbol{x}\). Instead we can measure three proxies, \(x_1\), \(x_2\) and \(x_3\) that are all quite similar to the true \(x\). One may think that this will not cause too many problems as we have not just one but multiple fairly precise variables.

15.2 Forward selection

There are several solutions to this problem. A popular algorithm is forward selection where one first picks the best 1-feature model, thereafter tries adding all remaining features one-by-one to build the best two-feature model, and thereafter the best three-feature model, and so on, until the model performance starts to deteriorate.

0-feature base model:

m0 = LinearRegression(fit_intercept = False)
X0 = np.ones((X.shape[0], 1))
X0t, X0v, yt, yv = train_test_split(X0, y, test_size = 0.4,
                                    random_state = 8)
_t = m0.fit(X0t, yt)
m0.score(X0v, yv)

## -0.006849647990198937

Try 1-feature models:

best1 = {"i": -1, "R2": -np.inf}
m1 = LinearRegression(fit_intercept = True)
for i in range(X.shape[1]):
    X1 = X.iloc[:,[i]]
    X1t, X1v, yt, yv = train_test_split(X1, y, test_size = 0.4,
                                    random_state = 8)
    _t = m1.fit(X1t, yt)
    s = m1.score(X1v, yv)
    if s > best1["R2"]:
        best1["i"] = i
        best1["R2"] = s
        
best1

## {'i': 9, 'R2': 0.4666428183761875}

Add another feature:

best2 = {"i": -1, "R2": -np.inf}
m2 = LinearRegression(fit_intercept = True)
included_features = set([best1["i"]])
features_to_test = set(range(X.shape[1])) - included_features
for f in features_to_test:
    features = included_features.union({f})
    X2 = X.iloc[:, list(features)]
    X2t, X2v, yt, yv = train_test_split(X2, y, test_size = 0.4,
                                    random_state = 8)
    _t = m2.fit(X2t, yt)
    s = m2.score(X2v, yv)
    if s > best2["R2"]:
        best2["i"] = f
        best2["R2"] = s
        
best2

## {'i': 2, 'R2': 0.8677935861014889}

Can add more in this fashion.

Make a function:

def bestFeature(X, y, included_features):
    best = {"i": -1, "R2": -np.inf}
    features_to_test = list(
        set(range(X.shape[1])) - set(included_features))
    for f in features_to_test:
        features = included_features + [f]
        Xf = X.iloc[:, features]
        Xft, Xfv, yt, yv = train_test_split(Xf, y, test_size = 0.4,
                                            random_state = 8)
        _t = m2.fit(Xft, yt)
        s = m2.score(Xfv, yv)
        if s > best["R2"]:
            best["i"] = f
            best["R2"] = s
    return best

best = list()
included_features = []
r2s = []
for f in range(X.shape[1]):
    b = bestFeature(X, y, included_features)
    best.append(b)
    included_features = included_features + [b["i"]]
    r2s.append(b["R2"])
best

## [{'i': 9, 'R2': 0.4666428183761875}, {'i': 2, 'R2': 0.8677935861014889}, {'i': 27, 'R2': 0.9296522813032738}, {'i': 28, 'R2': 0.9396723227644169}, {'i': 14, 'R2': 0.9430611422142994}, {'i': 22, 'R2': 0.9437993501430608}, {'i': 33, 'R2': 0.9446022123630592}, {'i': 59, 'R2': 0.9450369454683462}, {'i': 10, 'R2': 0.9452498568205782}, {'i': 8, 'R2': 0.9455986815032276}, {'i': 19, 'R2': 0.9462862467428159}, {'i': 1, 'R2': 0.9464320773146165}, {'i': 46, 'R2': 0.9465914853888853}, {'i': 40, 'R2': 0.9465889082229213}, {'i': 55, 'R2': 0.9465359196145449}, {'i': 36, 'R2': 0.9464542982901596}, {'i': 5, 'R2': 0.9463762822853345}, {'i': 20, 'R2': 0.9462833979835922}, {'i': 34, 'R2': 0.9462050456158057}, {'i': 48, 'R2': 0.9461478229257206}, {'i': 50, 'R2': 0.9461054197700751}, {'i': 52, 'R2': 0.9460730478692239}, {'i': 26, 'R2': 0.9459904691472554}, {'i': 42, 'R2': 0.9459265694540916}, {'i': 44, 'R2': 0.9458087497124463}, {'i': 32, 'R2': 0.9455590142220006}, {'i': 39, 'R2': 0.945408502141411}, {'i': 25, 'R2': 0.9449675269753557}, {'i': 24, 'R2': 0.9445346914386826}, {'i': 58, 'R2': 0.9438665545550707}, {'i': 54, 'R2': 0.9431161004717253}, {'i': 38, 'R2': 0.9425908604390918}, {'i': 21, 'R2': 0.9418808150038418}, {'i': 35, 'R2': 0.9414073375383587}, {'i': 37, 'R2': 0.9410776069690762}, {'i': 41, 'R2': 0.940836636399586}, {'i': 49, 'R2': 0.9406534112839524}, {'i': 51, 'R2': 0.940509615245991}, {'i': 53, 'R2': 0.9403938540834724}, {'i': 43, 'R2': 0.9401119255355864}, {'i': 57, 'R2': 0.9397885757150655}, {'i': 23, 'R2': 0.9394085387576068}, {'i': 12, 'R2': 0.9379313435724337}, {'i': 30, 'R2': 0.9377835490332745}, {'i': 45, 'R2': 0.9333091167915868}, {'i': 29, 'R2': 0.9340676090843362}, {'i': 16, 'R2': 0.9285874234675286}, {'i': 0, 'R2': 0.9182942310441039}, {'i': 6, 'R2': 0.880809369532485}, {'i': 56, 'R2': 0.8437760019671372}, {'i': 31, 'R2': 0.8474899063079687}, {'i': 47, 'R2': 0.8521445384395225}, {'i': 17, 'R2': -9.818297650553768e+22}, {'i': 13, 'R2': -2.000001247173613e+22}, {'i': 15, 'R2': -4.135131612681403e+22}, {'i': 3, 'R2': -2.7600188239712023e+22}, {'i': 4, 'R2': -1.1141317933826631e+23}, {'i': 7, 'R2': -5.35812572220869e+22}, {'i': 18, 'R2': -3.2569968014607136e+22}, {'i': 11, 'R2': -3.4476870254964047e+22}]

plt.s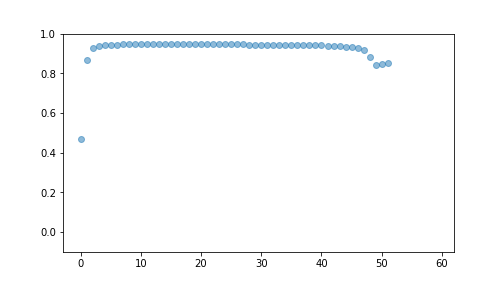catter(range(len(r2s)), r2s, alpha = 0.5)
plt.ylim(-0.1, 1)

## (-0.1, 1.0)

plot of chunk unnamed-chunk-10

from sklearn.feature_selection import SequentialFeatureSelector

m = LinearRegression()
sfs = SequentialFeatureSelector(m)
_t = sfs.fit(Xt, yt)
sfs.get_feature_names_out()

## array(['x3', 'x10', 'z1_B', 'z1_C', 'z2_B', 'z2_C', 'z4_B', 'z4_C',
##        'z5_B', 'z6_B', 'z7_B', 'z7_C', 'z8_B', 'z10_B', 'z10_C', 'z12_B',
##        'z12_C', 'z13_B', 'z13_C', 'z14_B', 'z14_C', 'z15_B', 'z15_C',
##        'z16_B', 'z17_B', 'z18_B', 'z18_C', 'z19_B', 'z20_B', 'z20_C'],
##       dtype=object)

Xtr = sfs.transform(Xt)
Xvr = sfs.transform(Xv)
_t = m.fit(Xtr, yt)
m.score(Xvr, yv)

## 0.9329183739713025

15.3 Ridge and Lasso regression

Ridge and Lasso are methods that are related to forward selection. These methods penalize large \(\beta\) values and hence suppress or eliminate correlated variables. These do not need looping over different combinations of variables like forward selection, however, one normally has to loop over the penalty parameter alpha to find the optimal value.

Both methods are living in sklearn.linear_regression. We demonstrate this with ridge regression below:

from sklearn.linear_model import Ridge, Lasso

m = Ridge(alpha = 1)  # penalty value 1
cross_val_score(m, X, y, cv=10).mean()

## NameError: name 'cross_val_score' is not defined

m = Ridge(alpha = 0.3)  # penalty value 0.1
cross_val_score(m, X, y, cv=10).mean()

## NameError: name 'cross_val_score' is not defined

As evident from the above, penalty values 1 and 0.3 give virtually equal results. The cross-validated \(R^2\) is also comparable to what forward-selection suggested.

Lasso works in an analogous fashion as ridge, but as it’s penalty is not globally differentiable (it is \(L_1\) penalty), then you may run into more problems with convergence.

Both methods have more options, in particular they can normalize the features before fitting.

m = Ridge(alpha = 1)
_t = m.fit(Xt, yt)
m.score(Xv, yv)

## 0.9264571331356263

m = Lasso(alpha = 1)
_t = m.fit(Xt, yt)
m.score(Xv, yv)

## 0.8627943726880424