Chapter 14 Machine Learning Workflow

We assume you have loaded the following packages:

import numpy as np
import pandas as pd

## /home/otoomet/R/x86_64-pc-linux-gnu-library/4.4/reticulate/python/rpytools/loader.py:120: UserWarning: Pandas requires version '1.3.6' or newer of 'bottleneck' (version '1.3.5' currently installed).
##   return _find_and_load(name, import_)

import matplotlib.pyplot as plt

Below we load more as we introduce more.

In this section we walk over a typical machine learning workflow using sklearn package. We assume you know what is overfitting and validation (see Section 13) and you are familiar with the basics of sklearn (see Section 10.2.2).

14.1 Boston Housing Data

Here we demonstrate small task to select the best linear regression model using validation. We use Boston Housing Dataset.

boston = pd.read_csv("../data/boston.csv.bz2", sep="\t")
boston.head(3)

##       crim    zn  indus  chas    nox  ...  tax  ptratio   black  lstat  medv
## 0  0.00632  18.0   2.31     0  0.538  ...  296     15.3  396.90   4.98  24.0
## 1  0.02731   0.0   7.07     0  0.469  ...  242     17.8  396.90   9.14  21.6
## 2  0.02729   0.0   7.07     0  0.469  ...  242     17.8  392.83   4.03  34.7
## 
## [3 rows x 14 columns]

Our task is to predict the average house value medv as well as we can using all other features. We pick a subset of features

boston = boston[["age", "rm", "zn", "medv"]]

And we add a few features, namely \(\mathit{age}\times\mathit{rm}\) and

boston["ageXrm"] = boston.age * boston.rm

Now we have dataset that looks like

boston.sample(3)

##       age     rm   zn  medv    ageXrm
## 357  91.0  6.395  0.0  21.7  581.9450
## 337  59.6  5.895  0.0  18.5  351.3420
## 327  43.7  6.083  0.0  22.2  265.8271

First we demonstate the workflow using training-validation approach. We split data into training and validation parts:

from sklearn.model_selection import train_test_split

y = boston.medv
X = boston[["age", "rm", "zn", "ageXrm"]]
yt, yv, Xt, Xv = train_test_split(y, X)

Now we can test different models in terms of \(R^2\):

from sklearn.linear_model import LinearRegression

m = LinearRegression()
_t = m.fit(Xt, yt)
m.score(Xv, yv)

## 0.6643403222457258

This was the model with all variables. We can try other combinations of variables:

X = boston[["age", "rm", "zn"]]  # leave out age x rm
yt, yv, Xt, Xv = train_test_split(y, X)
_t = m.fit(Xt, yt)
m.score(Xv, yv)

## 0.43449053972781615

and

X = boston[["rm"]]  # use only rm
yt, yv, Xt, Xv = train_test_split(y, X)
_t = m.fit(Xt, yt)
m.score(Xv, yv)

## 0.45337488549300176

14.2 Categorization: image recognition

Here we analyze MNIST digits. This is a dataset of handwritten digits, widely used for computer vision tasks. sklearn contains a low-resolution sample of this dataset:

from sklearn.datasets import load_digits
mnist = load_digits()
X = mnist.data
y = mnist.target

This loads the dataset and extracts the design matrix and labels y from there. We can take a look how does the data look with

X.shape

## (1797, 64)

y[:25]

## array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 1,
##        2, 3, 4])

X tells us that we have 1797 different digits, each of which contains 64 features. These features are pixels–the image consists of \(8\times8\) pixels, in the design matrix X the images are flattened into 64 consecutive pixels as features. A sample of data looks like

X[7:9]

## array([[ 0.,  0.,  7.,  8., 13., 16., 15.,  1.,  0.,  0.,  7.,  7.,  4.,
##         11., 12.,  0.,  0.,  0.,  0.,  0.,  8., 13.,  1.,  0.,  0.,  4.,
##          8.,  8., 15., 15.,  6.,  0.,  0.,  2., 11., 15., 15.,  4.,  0.,
##          0.,  0.,  0.,  0., 16.,  5.,  0.,  0.,  0.,  0.,  0.,  9., 15.,
##          1.,  0.,  0.,  0.,  0.,  0., 13.,  5.,  0.,  0.,  0.,  0.],
##        [ 0.,  0.,  9., 14.,  8.,  1.,  0.,  0.,  0.,  0., 12., 14., 14.,
##         12.,  0.,  0.,  0.,  0.,  9., 10.,  0., 15.,  4.,  0.,  0.,  0.,
##          3., 16., 12., 14.,  2.,  0.,  0.,  0.,  4., 16., 16.,  2.,  0.,
##          0.,  0.,  3., 16.,  8., 10., 13.,  2.,  0.,  0.,  1., 15.,  1.,
##          3., 16.,  8.,  0.,  0.,  0., 11., 16., 15., 11.,  1.,  0.]])

You can see many “0”-s (background) and numbers between “1” and “15”, denoting various intensity of the pen. We can easily plot these images, just we have to reshape those back into \(8\times8\) matrices. This is what is leads to

X[7].reshape((8,8))

## array([[ 0.,  0.,  7.,  8., 13., 16., 15.,  1.],
##        [ 0.,  0.,  7.,  7.,  4., 11., 12.,  0.],
##        [ 0.,  0.,  0.,  0.,  8., 13.,  1.,  0.],
##        [ 0.,  4.,  8.,  8., 15., 15.,  6.,  0.],
##        [ 0.,  2., 11., 15., 15.,  4.,  0.,  0.],
##        [ 0.,  0.,  0., 16.,  5.,  0.,  0.,  0.],
##        [ 0.,  0.,  9., 15.,  1.,  0.,  0.,  0.],
##        [ 0.,  0., 13.,  5.,  0.,  0.,  0.,  0.]])

If you look at the matrix closely, you can see that it depicts a number “7”. This is much easier to see if we plot the result:

plt.imshow(X[7].reshape((8,8)), cmap="gray_r")

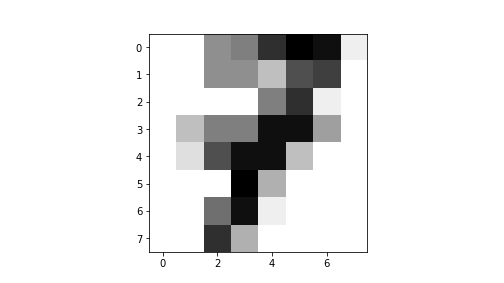
plot of chunk unnamed-chunk-15

This is a low-resolution image of number “7”. Here is a larger example of the first 30 digits:

for i in range(30):
    ax = plt.subplot(3, 10, i+1)
    _ = ax.imshow(X[i].reshape((8, 8)), cmap='gray_r')
    _ = ax.axis("off")
    _ = ax.set_title(f"A: {y[i]}")
_ = plt.show()

plot of chunk unnamed-chunk-16

As you can see, the numbers are of low quality and a bit hard to recognize for us. Computer will do it very well though–our brains are trained with high-quality images, not with low-quality images like here.

As a first step, let’s take an easy task and separate “0”-s and “1”-s. We’ll test a few different models in terms of how well do those perform. Extract all “0”-s and “1”-s:

## Find all 0,1 -s
i = np.isin(y, [0, 1])
Xd01 = X[i]
yd01 = y[i]

Next, we do training-validation split to validate our predictions:

Xt, Xv, yt, yv = train_test_split(Xd01, yd01)
Xt.shape, Xv.shape

## ((270, 64), (90, 64))

We can use logistic regression for this binary classification task, and after we fit the model, we compute accuracy:

from sklearn.linear_model import LogisticRegression

m = LogisticRegression()
_t = m.fit(Xt, yt)  # fit on 270 training cases
m.score(Xv, yv)  # validate on 90 validation cases

## 1.0

We got a perfect score–1.0. This means that the model is able to perfectly distinguish between these two digits. Indeed, these digits are in fact easy to distinguish, the pixel patterns look substantially different.

Let us try some more challenging tasks–to distinguish between “4”-s and “9”-s:

i = np.isin(y, [4, 9])
Xd01 = X[i]
yd01 = y[i]
Xt, Xv, yt, yv = train_test_split(Xd01, yd01)
_t = m.fit(Xt, yt)
m.score(Xv, yv)

## 0.989010989010989

The result is still ridiculously good with only a single wrong prediction as shown by the confusion matrix:

from sklearn.metrics import confusion_matrix
yhat = m.predict(Xv)
confusion_matrix(yv, yhat)

## array([[38,  1],
##        [ 0, 52]])

The mis-categorized image is

iw = yhat != yv  # which predictions are wrong
plt.imshow(Xv[iw].reshape((8, 8)), cmap='gray_r')

## <matplotlib.image.AxesImage object at 0x7529b6ad2630>

plt.axis("o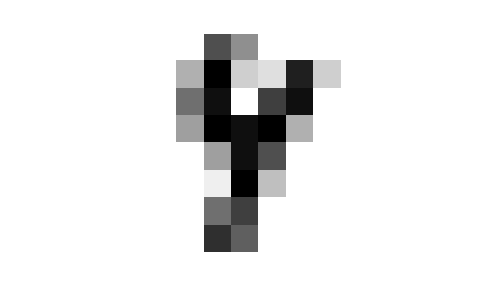ff")

## (-0.5, 7.5, 7.5, -0.5)

plt.show()

plot of chunk unnamed-chunk-22

Indeed, even human eyes cannot tell what is the digit.

Logistic regression allows to use more than two categories–this is called multinomial logit. So instead of distinguishing between just two types of digits, we can categorize all 10 different categories:

from warnings import simplefilter
from sklearn.exceptions import ConvergenceWarning

simplefilter("ignore", category=ConvergenceWarning)

Xt, Xv, yt, yv = train_test_split(X, y)
m = LogisticRegression()
_t = m.fit(Xt, yt)
m.score(Xv, yv)

## 0.96

The results are still very-very good although we got more than a single case wrong. The confusion matrix is

yhat = m.predict(Xv)
confusion_matrix(yv, yhat)

## array([[52,  0,  0,  0,  0,  0,  0,  0,  0,  0],
##        [ 0, 34,  0,  0,  2,  0,  1,  0,  1,  0],
##        [ 0,  0, 34,  0,  0,  0,  0,  0,  0,  0],
##        [ 0,  0,  0, 41,  0,  1,  0,  0,  0,  0],
##        [ 0,  0,  0,  0, 55,  0,  0,  0,  0,  0],
##        [ 0,  0,  1,  0,  1, 41,  0,  2,  0,  2],
##        [ 0,  0,  0,  0,  0,  0, 49,  0,  0,  0],
##        [ 0,  0,  0,  0,  0,  0,  0, 46,  0,  1],
##        [ 0,  3,  1,  0,  0,  0,  0,  0, 38,  0],
##        [ 0,  0,  0,  0,  0,  0,  0,  0,  2, 42]])

We can see that by far the most cases are on the main diagonal–the model gets most of the cases right. The most problematic cases are mispredicting “8” as “1”.

14.3 Training-validation-testing approach

We start by separating testing, or hold-out data:

Xw, Xh, yw, yh = train_test_split(X, y)
Xw.shape

## (1347, 64)

Now we do not touch the hold-out data until the very end. Instead, we split the work-data into training and validation parts:

Xt, Xv, yt, yv = train_test_split(Xw, yw)
Xt.shape

## (1010, 64)

Now we can test different models on training-validation data:

mLogistic = LogisticRegression(C=1e9)
mLogistic.fit(Xt, yt)

## LogisticRegression(C=1000000000.0)

mLogistic.score(Xv, yv)

## 0.9495548961424333

The beauty of sklearn is that is easy to try different models. Let’s try a single nearest-neighbor classifier:

from sklearn.neighbors import KNeighborsClassifier

m1NN = KNeighborsClassifier(1)
_t = m1NN.fit(Xt, yt)
m1NN.score(Xv, yv)

## 0.9940652818991098

This one achieved very good score on validation data. What about 5-nearest neighbors?

from sklearn.neighbors import KNeighborsClassifier

m5NN = KNeighborsClassifier(5)
_t = m5NN.fit(Xt, yt)
m5NN.score(Xv, yv)

## 0.9910979228486647

The accuracy is almost as good as in single-nearest-neighbor case. We can also try decision trees:

from sklearn.tree import DecisionTreeClassifier

mTree = DecisionTreeClassifier()
_t = mTree.fit(Xt, yt)
mTree.score(Xv, yv)

## 0.8545994065281899

Trees were clearly inferior here.

Instead of training-validation split, we can use cross-validation:

from sklearn.model_selection import cross_val_score

cross_val_score(mLogistic, Xw, yw, cv=5).mean()

## 0.9524686768552939

cross_val_score(m1NN, Xw, yw, cv=5).mean()

## 0.9836596447748864

cross_val_score(m5NN, Xw, yw, cv=5).mean()

## 0.9821891780256093

cross_val_score(mTree, Xw, yw, cv=5).mean()

## 0.8188627288999036

Cross-validation basically replicated training-validation split results and the best model again appears to be 1-NN. But the lead in front of 5-NN is just tiny. But we can pick 1-NN as our preferred model.

Fianlly, the hold-out data gives us the final performance measure:

m1NN.score(Xh, yh)

## 0.9844444444444445

Now we have computed the final model accuracy, we should not change the model any more.