library(devtools)
devtools::install_github("dd-harp/ramp.xds")Solving Dynamical Systems
What does it mean to solve a malaria model?
After writing down a system of equations, we will want to start using it to do things. That could mean one of several things.
In the vignette, we did some basic analysis. This is the sort of analysis we would do in a math class using a pencil, paper, and basic algebra. If we extend this a bit, we’re doing something called stability analysis.
We could solve the equations, but what does that mean, exactly?
We could fit the models to data.
Parts
The Ross-Macdonald Model, as we presented it in the previous vignette is this system:
\[\begin{array}{rl} \frac{dx}{dt} &= mabz (1-x) - r x\\ \frac{dy}{dt} &= acx (1-y) - g y\\ \frac{dz}{dt} &= acx_\tau \; e^{-g\tau} (1-y_\tau) - g z\\ \end{array}\]We can identify various parts of the equation:
The independent variable is time \(t\).
The dependent variables are \(x(t),\) \(y(t),\) and \(z(t).\)
The model has several parameters: \(m, a, b, r, c, g\) and \(\tau.\) If we don’t specify the values of the parameters, we have a model family. To solve the dynamical system, we must assign values to all the parameters.
Solutions to dynamical systems are parametric curves describing the values of the dependent variables (e.g., triplets of values \[\left\{x\left(t\right), y\left(t\right),z\left(t\right)\right\}\] that satisfy the differential equations (above) for every value of the independent variable (time, \(t\)).
To solve the equations, we must supply the values of the variables at one point in time, \(t_0;\) \[\left\{x\left(t_0\right), y\left(t_0\right),z\left(t_0\right)\right\}.\] We call these the initial values.
Closed-Form Solutions
In some rare cases, we can find closed-form solutions to differential equations, including Lotka’s solution to Ross’s equations [1]. We have already presented a simple example:
\[\frac{dx}{dt} = h(1-x)-rx\] with the intial condition \(x(0) = x_0\) has the solution:
Numerical Solutions
To get solutions, we rely on numerical methods developed to solve dynamical systems. This is a part of simulation-based analytics that most malaria analysts will want to avoid. What analysts should know is that several very good software packages have been written to solve differential equations, including deSolve for R.
We have developed software that was designed for malaria analysts, an R package called ramp.xds with several supporting satellite packages. A website to support Simulation-Based Analytics called SimBA was developed as a companion to this one. That software makes it easy to build and solve dynamical systems models for malaria, such as the Ross-Macdonald Model.
First install:
The load:
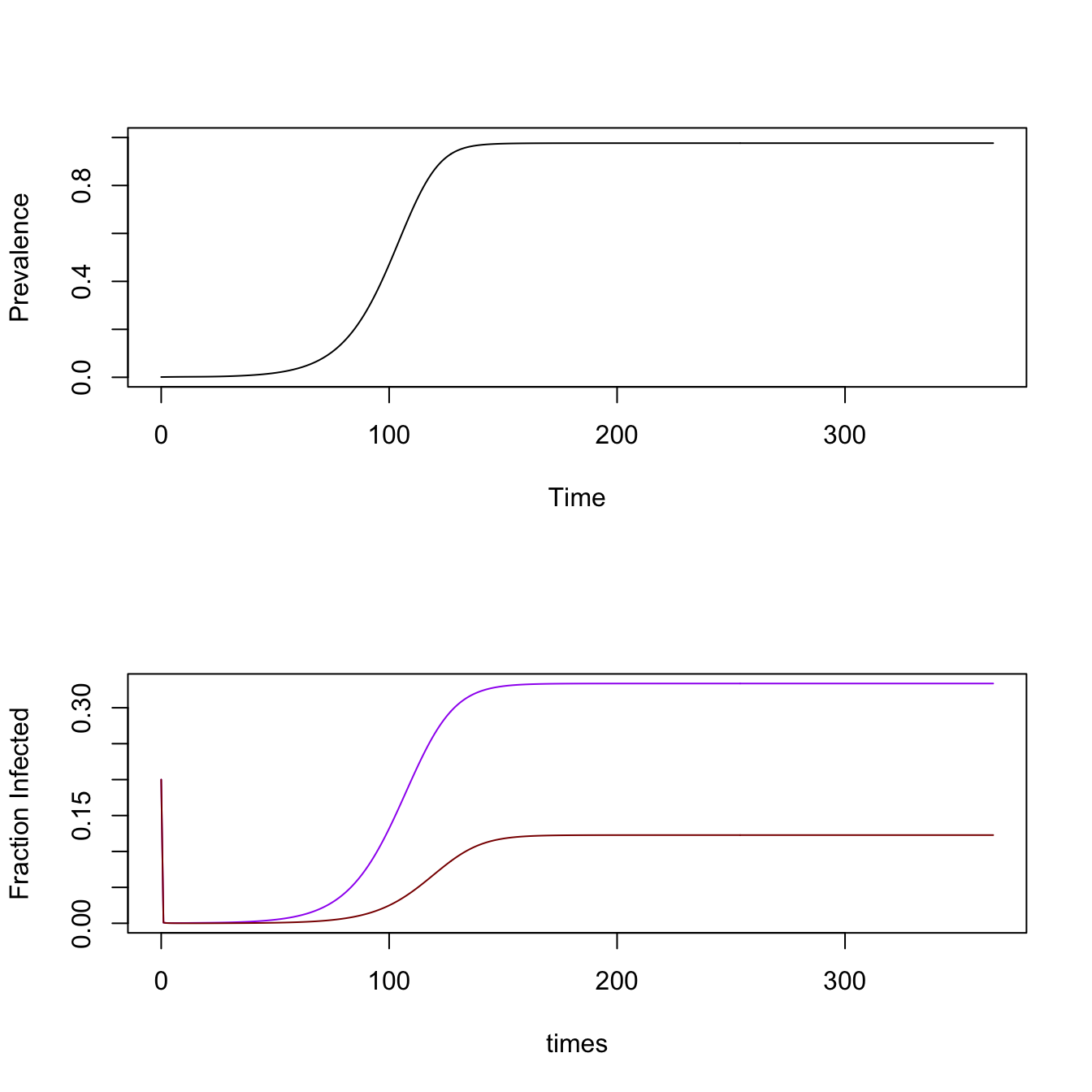
library(ramp.xds)A version of the Ross-Macdonald model is the default, so it is easy to set it up and solve it:
mod <- xds_setup()
mod <- xds_solve(mod)and then we can plot the outputs:
par(mfrow = c(2,1))
xds_plot_PR(mod)
xds_plot_Y_fracs(mod)
xds_plot_Z_fracs(mod, add=T)
References
1.