Beyond-Bandwidth Control in High-Speed Precision Mechatronics

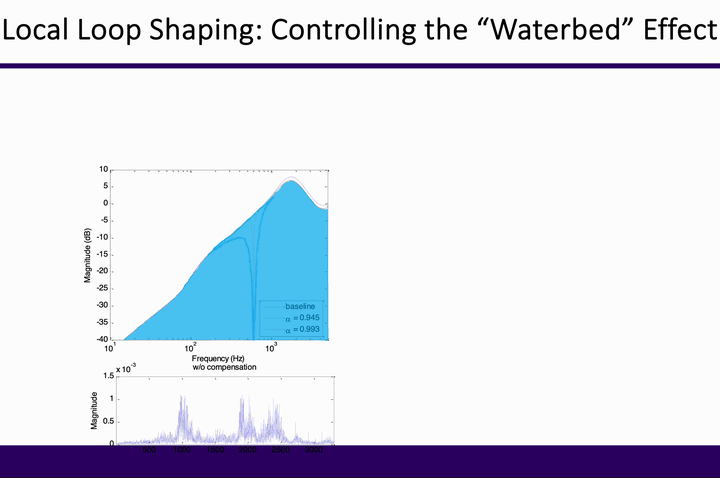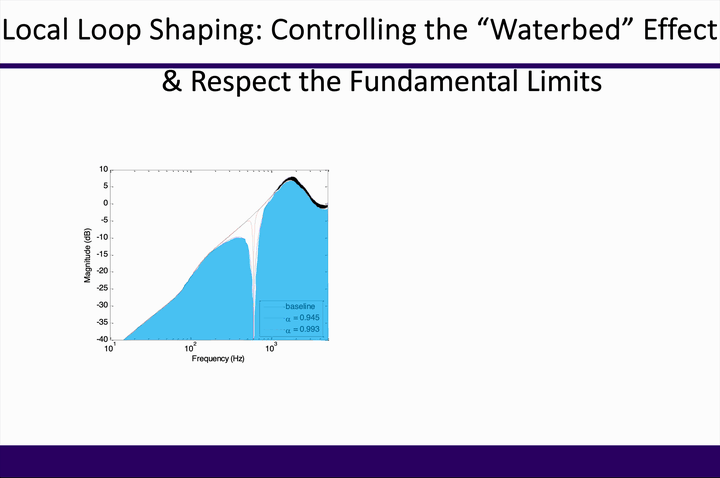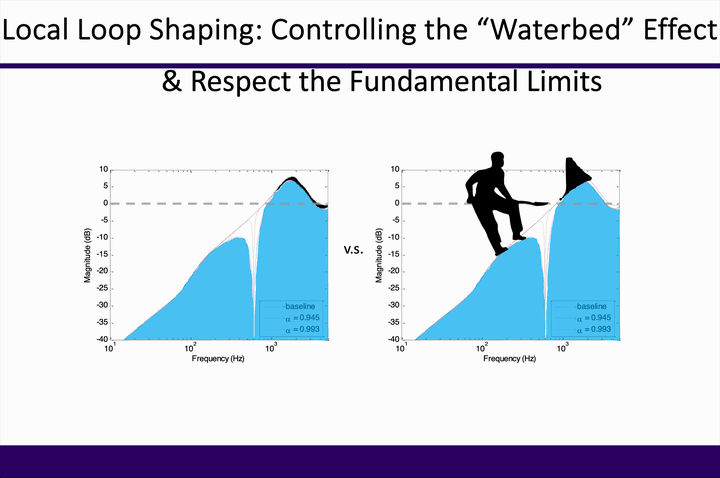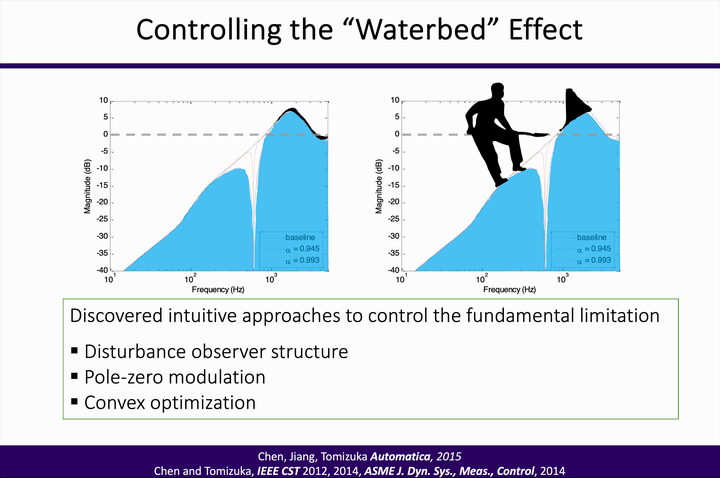
“Imagine an airplane flying at 500,000 miles per hour but only 1/16 inch above the ground on a highway with 100,000 lanes where the width of each lane is only fraction of an inch. The challenge of the problem is further intensified by the fact that the airplane is expected to switch lanes frequently and then follow the new lane with the same precision. A scaled down version of this scenario is what one finds in the head positioning servomechanism of a (2007) hard disk drive.” (Al Mamun et al., CRC Press, 2007)

This work targets customizing feedback controls to the performance extreme for such mechatronic systems as nanometer-precision information storage, semiconductor manufacturing, and nascent laser-aided material processing in additive manufacturing.

At the center of feedback control here is the algebra for manipulating the closed-loop error rejection function. Although a sizable literature exists for such general-purpose feedback controls as low-frequency disturbance rejection, creating customized controls at multiple frequency bands that meet the industry’s extreme performance needs had remained an unsolved problem. One intrinsic challenge has been rising from the Bode’s Integral Theorem, which guarantees (under mild assumptions) the occurrence of error amplifications during shaping the feedback control loop.

Our key finding was that disturbance amplifications from fundamental limits of feedback control can be flexibly controlled with prescribed optimality and stability. In fact, such controls enabled to achieve high-performance operation far beyond the conventional closed-loop bandwidth when needed. Such framework of beyond-bandwidth local loop shaping has been deployed for nanometer-precision control in the information industry; the result at IEEE Transactions on Control Systems Technology was the 6th most cited single-/dual-authored paper in 2020 among the journal’s 202 publications in 2012.