Three different models are available in the VC to simulate the kinetics of DSB formation and repair:

1. LPL model (Curtis 1986)
2. RMR (Tobias 1985)
3. TLK (Stewart 2001)

Monophasic rejoining kinetics

In the LPL and RMR models, the rate of change in the number of DSB in a cell after an acute dose of radiation is modeled using the differential equation

dL(t)/dt = -lL(t) - hL(t)L(t).

Here, L(t) is the expected (average) number of unrejoined DSB in a cell at time t, l characterizes the first-order rejoining rate (rate proportional to L) and h characterizes the second-order rejoining rate (rate proportional to the square of L).  Both l and h have units of inverse time (e.g., h^-1). For the special case when the first-order rejoining rate is much faster than the second order rejoining rate [i.e., lL(t) >> hL(t)L(t)], the above differential can be well approximated by

dL(t)/dt = -lL(t)

When the irradiation time is very short compared to the half-time for DSB repair [=ln(2)/l], the amount of DNA damage present in the cell just after irradiation may be expressed as L(0) = SD, where D is the absorbed dose (Gy) and is the DSB yield per cell per unit dose of radiation.  The solution to the above differential equation is

L(t) = L(0)·exp{-lt)=SD·exp{-lt)

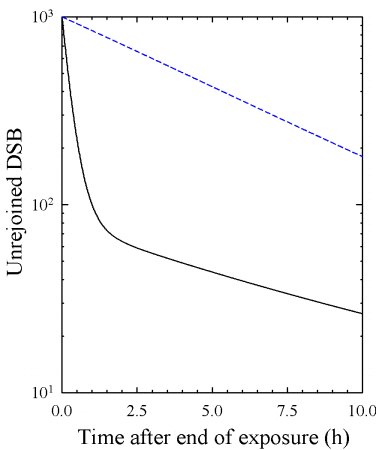
DSB rejoining kinetics is said to be monophasic when the number of unrejoined DSB as a function of time after irradiation can be modeled using a single exponential, as it is in this equation.

For most mammalian cells, the ratio l/h is typically greater 1,000, and the assumption that lL(t) >> hL(t)L(t) is often a quite good approximation.  Thus, DSB rejoining kinetics is effectively monophasic in the LPL and RMR models.  However, this approximation tends to break down as the dose becomes large and the irradiation time becomes short because the hL·L term increases faster than lL as L increases.  For large doses and short irradiation times, DSB rejoining kinetics is no longer monophasic in the LPL and RMR model because of the quadratic repair term becomes important (except of course for the special case h = 0).

Biphasic rejoining kinetics

Some experiments suggest that radiation effectively creates two or more kinds of DSB and each kind of DSB has its own unique repair characteristics (e.g., see Pastwa et al. 2003).  The TLK model is premised on the idea that radiation creates two kinds of DSB.  DSB rejoining kinetics is thus modeled using the following system of differential equations

dL₁(t)/dt = -l₁L₁(t) - hL₁(t)[L₁(t)+L₂(t)]
dL₂(t)/dt = -l₂L₁(t) - hL₂(t)[L₁(t)+L₂(t)]

In the above equations, the subscript 1 and 2 denote simple and complex DSBs, respectively.  Notice that each kind of DSB has its own characteristic first-order rejoining rate (l₁and l₂).  If we again invoke the assumption that the first-order rejoining rates are much faster than the second-order rejoining rate, the above equations reduce to

The solution to these equations, with L₁(0) = S₁D and L₂(0) = S₂D, is

L₁(t) = L₁(0)·exp{-l₁t)=S₁D·exp{-l₁t)
L₂(t) = L₂(0)·exp{-l₂t)=S₂D·exp{-l₂t)

In most if not all experiments, we cannot determine whether the DSB is a simple DSB or a complex DSB.  Instead, we only see the total number of unrejoined DSBs regardless of their complexity, i.e., we see the quantity L₁(t)+L₂(t).  From the above equations, it follows that the total number of unrejoined DSB at time t is

L(t) = L₁(t) + L₂(t) = S₁D·exp{-l₁t) + S₂D·exp{-l₂t)

From this equation, we see that the amount of residual damage is modeled using a sum of two exponentials, i.e., the rejoining kinetics is biphasic.  For the special case when l₁ = l₂, DSB rejoining kinetics effectively become monophasic.  Consequently, the TLK can be used to mimic the RMR by setting l₁ = l₂.  However, as with the LPL and RMR models, the quadratic repair terms become increasingly important in the TLK as L(t) increases and rejoining kinetics is no longer strictly monophasic or biphasic.

1. Paste the contents of RMR sample file #1 into a new ASCII input file called dsb1.inp. 
2. Set the absorbed dose to 1 Gy (AD=1), the irradiation time to 0.001 h (DOX=0.001), FSDX=0.1, TSAX=0.25 and TCUT=10.
3. Run the simulation with the -k command line switch.
4. Create a plot of the number of unrejoined DSB (y-axis, linear scale) vs. time (x-axis, linear scale).
5. Create a copy of the dsb1.inp file and rename it dsb2.inp.  In this input file, set the absorbed dose to 100 Gy and then re-run the simulation.  Create a second plot of the number of unrejoined DSB as a function of time time.

• Change the y-axis of the plots to a log scale.  Does the number of unrejoined DSB as a function of time appear to be a straight line for both the 1 and 100 Gy exposures (i.e., monophasic)?
• Set the pairwise damage interaction rate (h) to 0.1 (ETA=0.1) and the re-run 1 Gy simulation.  Update the plot (y-axis log scale, x-axis, linear scale).  Does the curvature of the line increase, decrease or stay the same?  If the curvature of the line changes, is quadratic repair (pairwise damage interaction) becoming less or more important?
• Set the pairwise damage interaction rate to zero (ETA=0) and the re-run 1 and 100 Gy simulations. Add the results from the new simulations (y-axis log scale, x-axis, linear scale).  Does the importance of the quadratic repair term increase, decrease or stay the same as time increases?

• In addition to the questions and studies suggested in Exercise 1, compare the shapes of the curves produced by the TLK to those produced by the RMR.  Is the solid black line in the figure shown below more appropriately described as monophasic, biphasic, or non-exponential (or multi-exponential)?  What about the blue dashed line?