1. Introduction to Thermodynamics
Thermodynamics is one of the best-established theories in all of science. It has survived multiple scientific revolutions and its staying power in large part arises from the very large number of interacting particles that give rise to the average macroscopic properties we measure such as volume, pressure, and temperature. In a chemical context, I find it particularly impressive that the laws of thermodynamics predate the atomic theory and have held true despite the fundamentally new understanding of the universe provided by the atomic theory. Using thermodynamics, we can better understand important aspects of chemical reactions, bioenergetics, enzymes, ligand binding, batteries, engines, refrigerators, and even the weather.
1.1. Thermodynamics Overview
Thermodynamics is an empirical theory for studying transfer of heat and work in ensembles of molecules. Empirical here means that the relationships are determined based more on observations than on theoretical derivations. In thermodynamics, we are typically studying matter that is at equilibrium, and we are less concerned with rates although there are important connections between equilibrium and rates that we will discuss later.
There are several key laws and definitions in thermodynamics that form the pillars holding the theory together. In this introduction we will review several of these.
1.1.1. Laws of Thermodynamics
The laws of thermodynamics are some of the most battle-tested and well-established ideas in all of science. In brief terms, they cover the following topics. We will go through these in more detail starting in the next section and in subsequent chapters.
Zeroth law: thermal equilibrium
First law: conservation of energy
Second law: defines entropy, direction of time, efficiency limits for converting work to heat
Third law: quantifies entropy
1.2. Zeroth Law of Thermodynamics
The first, second, and third laws are covered in subsequent chapters. Since the zeroth law does not require a full chapter, I will take a little time here to discuss it.
Why is it called the zeroth law? After the first, second, and third laws were developed, scientists realized that there was another important law that was foundational to the other three. Scientists began calling it by the slightly humorous name “the zeroth law” to recognize its foundational nature while avoiding renaming the other three laws. Fortunately, another foundational law hasn’t been identified, or else there might have been a bit of a conundrum about what to call it.
The zeroth law states that two objects that are each in thermal equilibrium with a third object are also in thermal equilibrium with each other. It is a type of transitive property, similar to relationships you have seen in a math course such as if \(A=B\) and \(B=C\) then \(A=C\).
The zeroth law statement seems relatively intuitive, and, frankly, will not be something we will actively invoke in our calcaulations, but it is important. It the simplest terms, it says that temperature is the property that determines whether two objects in thermal contact are in thermal equilibrium with each other. For instance, if the third object used to contact each of the other two objects is a thermometer, then it is able to determine whether the two objects are the same temperature. If they are in good thermal contact and have the same temperature, then the two objects are in thermal equilibrium.
Fig. 1.1 Thermal equilibration, temperature, and the zeroth law. And truly delicious ice cream.
1.3. Heat and Temperature
Heat, temperature, and work, are terms with specific meanings in thermodynamics and worth thinking about them carefully since they also occur in everyday speech.
Heat: Thermal energy which flows from a hotter object to a colder one. It is associated with the kinetic energy of the random motion of atoms and molecules. Its units are in Joules.
Temperature: We will simply define temperature as a measure of hotness or coldness (a course on statistical mechanics can provide a deeper understanding of temperature). Historically, temperature has been quantified in relation to specific reference points, such as the freezing and boiling points of water as 0 °C and 100 °C, respectively, and then interpolating or extrapoliting for other values. Our current reference points are absolute zero and the triple point of water, two ‘absolute’ reference points. We will typically use units of kelvin, K, or °C.
1.4. Gases
In my Physical Chemistry for Biochemists 1 course, students have occasionally asked “I am a biochemist…why should I study gases?” Although gases are arguably important for biochemistry (e.g., respiration, photosynthesis), we use them in thermodynamics because they convey key lessons with tractable math. Also, we can use liquid-gas equilibria to transfer a lot of our gas-phase tools to liquid phase studies. In any event, here are a couple of reminders for the study of gases.
An ideal gas consists of infinitesimally small particles that do not interact with each other, that collide elastically with their container, and that have random (isotropic) directions of motion…and that obeys the ideal gas equation of state \(PV=nRT\). While some real gases obey the IGL quite well within a certain regime (e.g., dilute, noble gases well above their boiling temperatures), other gases deviate prominently.
Most students already know how to use the ideal gas law well from their previous studies, but let’s take a minute to think about how good of an equation it is. It gives us a simple, intuitive way to relate important macroscopic properties without having to calculate them for individual particles. Just imagine you have \(~10^{24}\) particles (approximately one mole). To even load the positions and speeds (\(x\), \(y\), \(z\), \(v_x\), \(v_y\), \(v_z\)) into a computer (assuming \(~10^9\) numbers loaded per second) it would take on order of the age of the universe (which is \(~4\times 10^{17}\) sec), let alone simulate the motion of the gas, the collisions, or realistic intermolecular interactions! It would be hopelessly slow. In contrast, the ideal gas equation is easy to solve in a few seconds with a calculator!
Mixtures of noninteracting ideal gases are often approximated as obeying the ideal gas equation, now using \(P_i=n_iRT/v\), where \(P_i\) is the partial pressure of the \(i^\textrm{th}\) gas, \(n_i\) is the number of moles. The sum of the partial pressures is the total pressure and is given by \(P_\textrm{total}=P_1+P_2+P_3+ \cdots =\sum P_i\). The mole fraction is defined as \(x_i=n_i/n_\textrm{total}\), where \(n_\textrm{total}\) is the total number of moles of gas particles. It is also true that \(P_i=x_iP_\textrm{total}\).
Pressure refresher.
Questions: A cylinder with a piston of area 1 \(\textrm{m}^2\) has an initial volume of \(V=0\) (the piston is all the way closed). Calculate the following at sea level and 1 atm of ambient pressure. It is helpful to recall that 1 atm = 101325 Pa and \(R=8.31 \textrm{ J/(K mol)}\) and to use SI units (Section 1.6).
How much force does it take to pull th piston out to create a vacuum?
If the cylinder were pointed downwards, what is the minimum mass required for gravity to pull a vacuum with the piston? Use \(F=mg\) with \(g=9.8\textrm{ m/s}^2\).
Answers:
The problem provides an area and a pressure and these can be used to calculate the force from the definition of pressure as force per area, or \(P=F/A\).
so that
The mass required to create a force of 101325 N can be calculated using the force due to gravity \(F=mg\) as
At approximately the weight of two elephants, that is quite massive!
Quick practice calculations with mole fraction and partial pressure.
Questions: 1.5 mol of \(\require{mhchem}\ce{N2}\) and 0.5 mol of \(\ce{O2}\) are in a 5 L container at 400 K. Answer the following questions.
What is the mole fraction of \(\ce{N2}\)?
What is the partial pressure of \(\ce{O2}\)? Assume the gases behave ideally.
Answers:
We can evaluate the definition of mole fraction for this system.
We can calculate the partial pressure of \(\ce{O2}\) by multiplying mole fraction by the total pressure determined from the ideal gas law.
A van der Waals (vdW) gas is a minimal model for a real gas that is given by the following equation of state
It incorporates an \(a\) term that accounts for intermolecular interactions of gas particles and a \(b\) term that accounts for excluded volume from the nonzero size of gas particles. The \(a\) and \(b\) parameters are tabulated for different gases and, in general, are different for different gases.
1.5. Work
Work: (mechanical) work is the product of force over a distance. This can be extended for other types of work (e.g., pressure-volume work, electrical work) but we will focus on mechanical work.
When the force \(F\) is constant and applied over a distance \(x\), the work \(w\) is given by
More generally, for a force which may vary as a function of distance, the work from position \(x_1\) to \(x_2\) may be calculated using an integral as
where the force, \(F(x)\) is written to suggest a (possibly) position-dependent force.
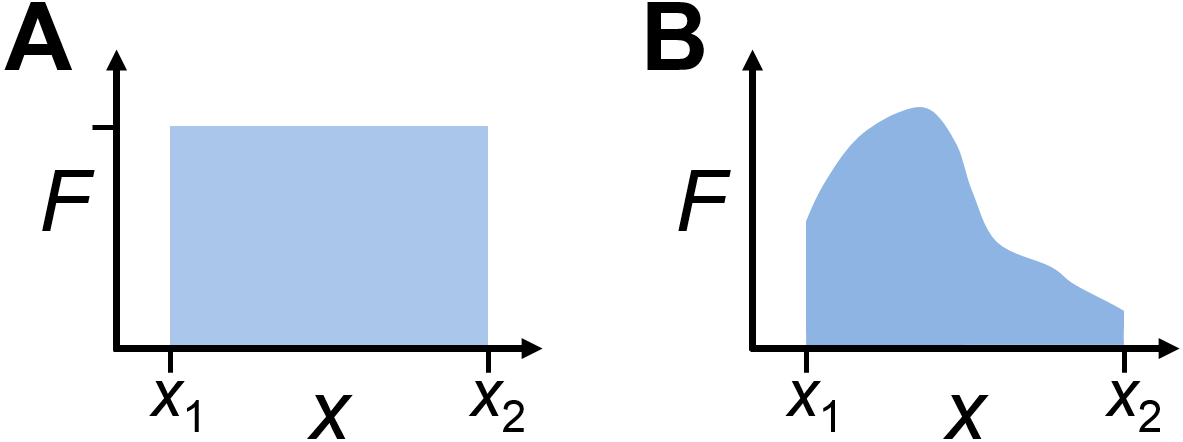
Fig. 1.2 Force-distance work is indicated by the area on a plot of force vs area. Examples of work done (shaded area) for A) constant or B) variable force.
You have probably thought about force-distance work in physics courses, but you may not have thought much about pressure-volume work. Let’s look at how to extend force-distance work to pressure-volume work. If you have gas in a piston that expands, say due to a chemical reaction, it will displace the piston some distance \(h\) against the external pressure \(P\).
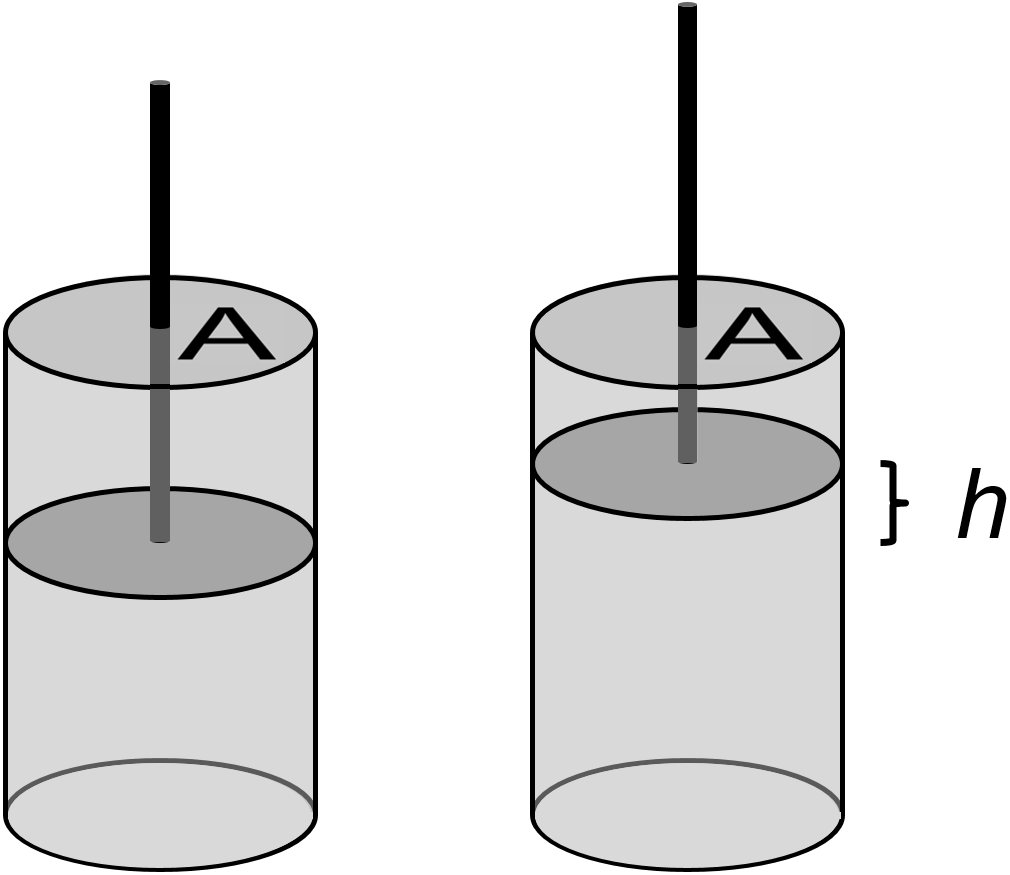
Fig. 1.3 Pressure-volume work in a piston with cross-sectional area \(A\) that is displaced distance \(h\).
If the piston has a cross-sectional area \(A\) and the force applied \(F\) is somehow constant over a distance \(h\), then the work can be expressed as, below
where the change in volume is given as the product of the piston area times displacement as \(\Delta V = Ah\), the definition of pressure (\(P=\frac{F}{A}\)) was used to give us \(F=PA\). Hopefully the basic connection between force-distance work and pressure-volume work is clear.
Next, I want to refine our pressure-volume work equation a bit, so I have rewritten it, below (Eq. (1.2)), with three modifications. First, I have written it as an integral to cover the possibility of variable pressure. Note that if pressure is constant, then the work will be proportional to \(P\Delta V\), as before. Second, I have introduced a minus sign to the equation, which is an important sign convention in chemical and biochemical thermodynamics. This minus sign causes work to be negative for expansions and positive for compressions. Can you see that if there is a compression, \(\Delta V<0\) and \(w>0\) but that if there is an expansion, \(\Delta V>0\) and \(w<0\)? (If there is no volume change, then \(\Delta V = 0\) and \(w=0\).) It helps me to keep this sign convention straight in my head when I describe work as work done on the system. Third, I have written the pressure as \(P_\textrm{ext}\) rather than just \(P\), where we use ‘external’ to indicate the external pressure that is key to calcaulating the work. For expansion, if a gas initially at 1 atm were expanded against an external pressure of 0.1 atm, the external pressure to use for calculation would be 0.1 atm. In the case of a compression, if the surrounding pressure were constant at 1 atm but the system pressure were 0.1 atm, then 1 atm should be used for the external pressure in the work calculation. It is important to use the external pressure for calculations. Note that if a gas were expanded into a vacuum, then the external pressure would be zero and no work is done.
Practice work calculations.
Questions: Calculate the amount of force-distance work or pressure-volume work done each of the following problems.
How much work done when applying a constant force of 9.8 N over a distance of 1 m?
How much work is done when pulling a spring with force constant k=4 N/m from 5 m to 6 m? Use Hooke’s law \(F=kx\) (we will just use a positive sign here for force).
How much work is done when slowly compressing a gas from a volume of \(\textrm{6 m}^3\) to \(\textrm{5 m}^3\) against a constant pressure of 1 atm? Be careful with units; for work calculations, the SI (International System) unit of pressure of Pa is usually easier (where 1 atm = 101325 Pa).
What is the work done to slowly compress 2 moles of ideal gas from \(\textrm{6 m}^3\) to \(\textrm{5 m}^3\) at 400 K?
Answers:
The constant force case is easily calculated, as below.
For a variable force, we need to use the integral form of the work calculation here.
For constant pressure, no integral is required.
Here we will use the integral version to calculate pressure-volume work since the pressure is variable. Additionally, we will note that since an ideal gas is specified, we can use the ideal gas equation for pressure \(P=nRT/V\).
1.6. Units
Units can either be your best friend or your worst enemy. If you take time to keep track of them, they will often guide you (e.g., if you were asked for an energy but obtain a force, then you should check your calculation). If you ignore units and hope everything works out, they will sometimes let you down (e.g., you weren’t paying attention and plugged in Celsius instead of Kelvin, giving you a major error).
We will generally use SI units, including kg, m, s, K as the fundamental units of mass, distance, time, and temperature. Then functions of these for force (N, newtons), energy (J, joules), power (W, watts), pressure (Pa, pascal), and volume (\(\textrm{m}^3\)). See also the glossary for a list of variables, constants, and their units. It is a good skill to be fluent at converting units, as well, for instance \(\textrm{N=kg m/s}^2\) or \(\textrm{Pa=N/m}^2\).
I find that students are often reluctant to give up the use of measuring volume in L, pressure in atm, where the gas constant is mostly easily used with units like this \(R=0.08206 \frac{\textrm{L atm}}{\textrm{K mol}}\). It’s certainly not wrong to work with these units, since all proper units systems when used correctly are equally valid, but it can be cumbersome and unintuitive to work with L and atm. If a gas expands by 5 L against a constant pressure of 2 atm, how much work is done? First off, most students are unaware that pressure times volume gives units of energy. Second, it takes a bit of effort to determine that there are 101.3 Joules per \(\textrm{L}\times \textrm{atm}\). However, converting 5 L and 1 atm to SI units (0.005 \(\textrm{m}^3\) and 101325 Pa) allows practitioners to benefit from the easy interchangeability of SI units since \(\textrm{m}^3\times \textrm{Pa} = \textrm{m}^3\times \textrm{N/m}^2=\textrm{J}\). SI units offer many advantages, so give it a try!
1.7. Additional Problems
1.7.1. Joule’s Honeymoon (story and problem)
One of James Prescott Joule’s crowning achievements was establishing the inter-conversion of different forms of energy, a principle that we now recognize as the conservation of energy. In a classic experiment, he churned water with a paddle and measured its increase in temperature. He was so proud of the ‘mechanical equivalent of heat’ that he selected his measurement of the heat capacity of water to be inscribed on his grave stone.
While Joule, a brewer by trade, was on his honeymoon in France, legend has it that he encountered William Thompson (later known as Lord Kelvin) and they attempted to measure the temperature difference of water at the top and bottom of a waterfall. Although the measurement was apparently unsuccessful, perhaps due to evaporation and wind resistance confounding the measurement, Joule and Kelvin ended up corresponding extensively on the subject of the nature of heat and you probably recognize that the units joule and kelvin were named in honor of the two scientists for their contributions to this and other work.
Let’s consider the waterfall idea from Joule and Kelvin. Specifically, how large of a temperature increase could possibly be achieved by the largest waterfall in the world, Angel Falls in Venezuela, with a spectacular 979 m drop? Use \(\overline{C}_P=4180 \textrm{ J/(K kg)}\) for the heat capacity of water and relate the gravitational potential energy to heat to determine the largest possible temperature change in the absence of evaporation or wind resistance.
Joule’s Honeymoon SOLUTION
We are consdiering the situation where the energy due to falling will be completely converted into heating of water. We can do that as follows. This uses the concept of heat capacity of water that will be formally introduced later in this textbook, but most students would have encountered the idea previously.
Next, solving for the temperature change and substituting in values we obtain a fairly large temperature jump.
Even the ~270 m free fall of the Cascade de l’Arpenaz waterfall near Chamonix where Joule and Kelvin would have had a 0.63 K temperature increase if there had been no confounding factors.