Machine Learning and Sparsity for Flow Control
LOADING
-
Bifurcation Structure for Large Amplitude Standing Water Waves
-
Machine Learning and Compressive Sensing for Flow Over a Cylinder
-
Compressive Sensing Architecture for Classification of Fluid Flow
-
Multi-Resolution Analysis for Extracting Multi-Scale Flows
-
Pressure Field for Flow Around a Cylinder
-
Spatio-Temporal Patterns of Pressure on Cylinder with Flow Around It
-
Principal Component Modes of Pressure for Flow Around Cylinder
Machine Learning in Fluid Dynamics
Time-varying fluid flows are ubiquitous in modern engineering and in the life sciences. Particularly challenging is the characterization of unsteady aerodynamic forces and moments as they play critical roles in, for instance, biological propulsion and bio-inspired engineering design principals. It is observed that birds, bats, insects, and fish routinely harness unsteady fluid phenomena to improve their propulsive efficiency, maximize thrust and lift, and increase maneuverability. Such observations are highly suggestive, leading to conjectures about the existence of low-dimensional structures in fluid flows. Machine learning aims to capitalize on such dominant patterns of spatio-temporal activity. When integrated with more traditional first-principals simulation, reduced-order models can be developed to accurately quantify fluid flows.
Compressive Sensing and Sparsity for Sensors
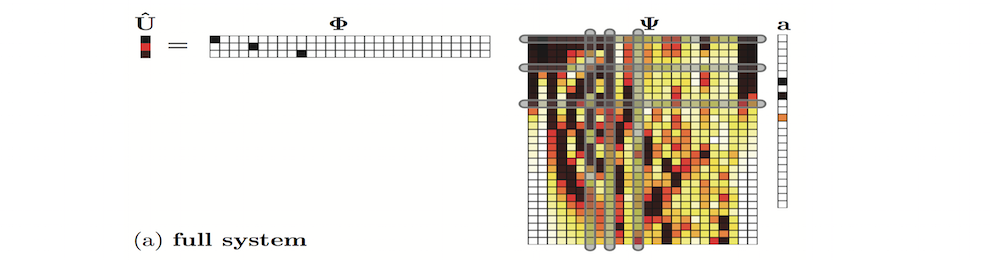
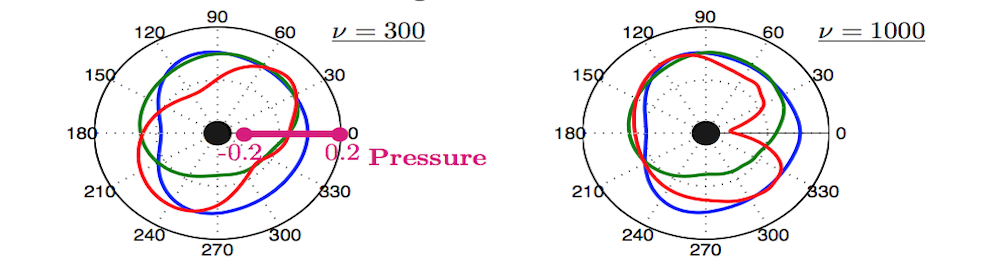
For many insects, robust flight dynamics and control is achieved despite potentially large perturbations in flight conditions (e.g., wind gusts, bodily harm). Such stable flight is accomplished despite their limited number of computational resources and spatially distributed, noisy sensors. It suggests that the low-dimensional structures in the flow-field that are sparsely sampled and exploited for robust control purposes. Our goal is to develop a mathematical framework for directly addressing this conjecture. In particular, we consider the model problem of flow around a cylinder where (i) dimensionality reduction is used to encode the low-dimensional dynamics present in the system for a wide range of fluid flows, and (ii) compressive (sparse) sampling is used to robustly decode the dynamic state of the system, thus revealing a promising, low-dimensional control architecture. The integration of such encoding (machine learning) and decoding (compressive sensing) strategies represents a novel approach for characterizing complex dynamical systems and/or fluid flows. Indeed, this approach presents a tremendous opportunity to develop the underlying mathematical theory of dynamical systems in the context of sparse data assimilation and machine learning.
Flow Control via Machine Learning and Equation-Free Controllers
Machine learning and compressive sensing provide a mathematical infrastructure that is ideal for applying and developing control laws. The machine learning provides the low-rank representation of the fluid flow, allowing for an efficient, low-dimensional control protocol. Compressive sensing can be used towards characterizing the best measurement and actuation locations capable of optimally, and with minimal actuation, manipulating the fluid flow. We continue to innovate new ideas around the integration of these methods, especially with equation-free protocols like extremum seeking controllers, towards building a better understanding of how bio-inspired flight control might occur.
Recent Selected Publications
- I. Bright, G. Lin and J. N. Kutz, Classification of Spatio-Temporal Data via Asynchronous Sparse Sampling: Application to Flow Around a Cylinder, arXiv:1506.00661.
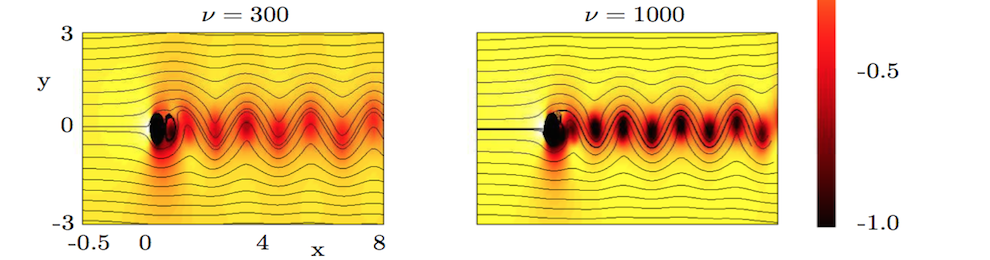
- I. Bright, G. Lin and J. N. Kutz, Compressive sensing based machine learning strategy for characterizing the flow around a cylinder with limited pressure measurements, Physics of Fluids 25 (2013) 127102.
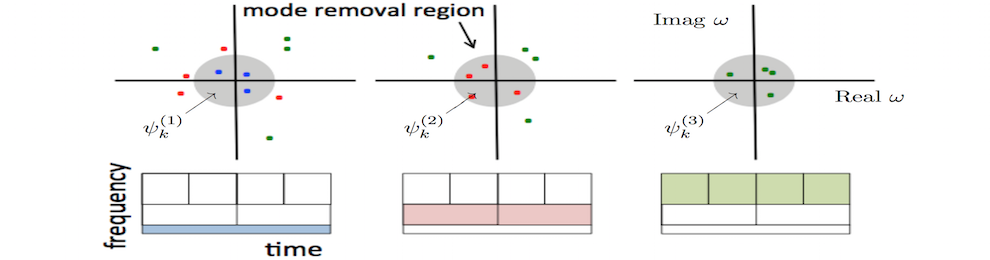
- J. Proctor, B. Brunton, S. Brunton and J. N. Kutz, Exploiting sparsity and equation-free architectures in complex systems, European Physics Journal Special Topics 223 (2014) 2665-2684.
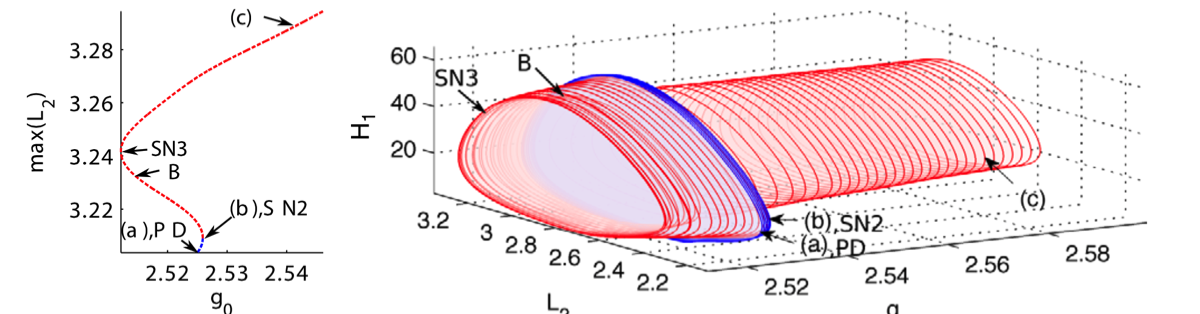
- S. Brunton, J. Tu, I. Bright and J. N. Kutz, Compressive sensing and low-rank libraries for classification of bifurcation regimes in nonlinear dynamical systems, SIAM Journal of Applied Dynamical Systesm 13 (2014) 1716-1732.
- J. Tu, C. Rowley, J. N. Kutz and S. Shang, Spectral analysis of fluid flows using sub-Nyquist-rate PIV data, Experiments in Fluids 55 (2014) 1805:1-13.