Leveraging Compressive Sensing and Sparse Representation in Dynamical Systems
LOADING
Data-Driven Discovery of Dynamical Systems via Sparsity
The ability to discover physical laws and governing equations from data is fundamental for a quantitative understanding of dynamic constraints and balances in nature. It is also critical for advancing technology. We have recently combined sparsity-promoting techniques and machine learning with nonlinear dynamical systems to discover governing physical equations from measurement data. The only assumptions we make are that there are only a few important terms that govern the dynamics, so that the equations are sparse in the space of possible functions. We can then use a sparse regression to determine the fewest and best terms in a dynamical system that accurately represent the data. The resulting models are parsimonious, balancing model complexity with descriptive ability while avoiding overfitting. This has tremendous potential for application across the engineering, physical and biological sciences.
Multi-Scale Physics and Sparsity
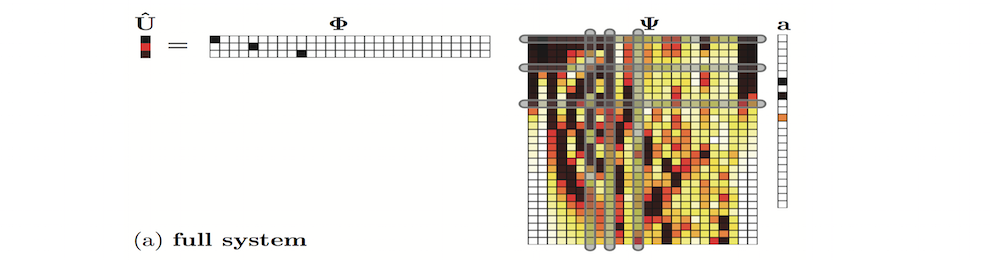
Compressive sensing and sparse representation take advantage of low-dimensional (compressive) representations of data. We have demonstrated in recent work that dimensionality-reduction in dynamical systems partners naturally with sparse sensing schemes since the low-rank basis modes naturally represent the data in a compressed manner. Multi-scale physics poses many unsolved and interesting challenges, especially in its data mixes different spatio-temporal scales. Separating these multi-scale phenomenon and looking for sparse representation at each scale is of importance for sparse sampling schemes. Moreover, it builds on the mathematical architectures we have built around these ideas.
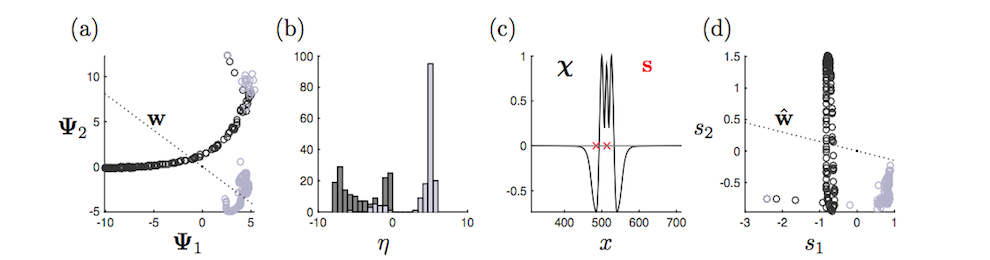
Classification of Dynamical States and POD Reconstructions
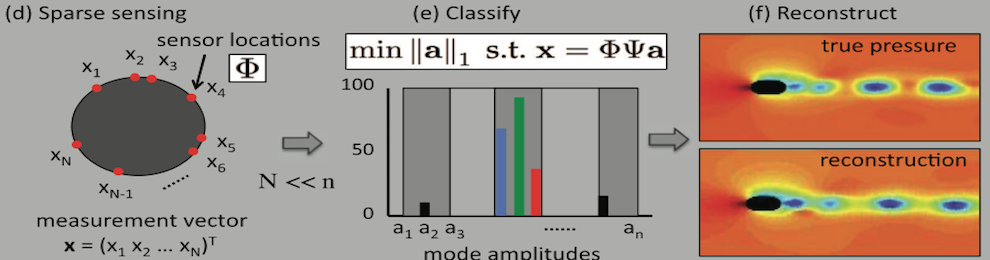
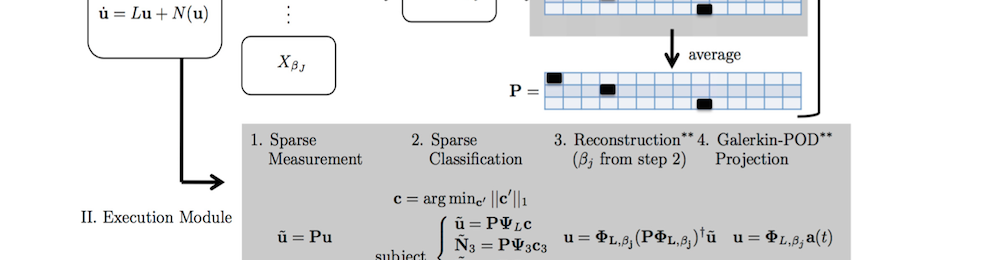
We are developing a general theoretical framework for nonlinear dynamical systems whereby low-rank libraries representing the optimal modal basis are constructed, or learned, from snapshot sampling of the dynamics. In order to make model reduction methods such as proper orthogonal decomposition (POD) computationally efficient, especially in evaluating the inner products of the nonlinear terms of the governing equations, sparse sampling is applied. Such sparse sampling of the nonlinearity is directly related to compressive sensing strategies whereby a small number of sensors can be used to characterize the dynamics of the nonlinear system. Indeed, the POD method, when combined with compressive sensing, can (i) correctly identifying the dynamical parameter regime, (ii) reconstruct the full state dynamics and (iii) produce a low-rank prediction of the future state of the nonlinear dynamical system. All of these tasks are accomplished in a low-dimensional way, unlike standard POD-Galerkin models whose nonlinearities can prove to be computationally inefficient.
Connections of Compressive Sensing to Gappy POD and DEIMs
Reconstruction from a limited number of measurements has been around since the seminal work of Everson & Sirovich in 1995 on the Karhunen-Loeve procedure for gappy data. Indeed, this procedure is at the heart of gappy POD methods which attempt to reconstruct inner products of nonlinear functions in a highly-efficient manner. The Discrete Empirical Interpolation Method (DEIM) of Chaturantabut and Sorensen builds upon this concept by developing a greedy algorithm for efficiently evaluating such inner products. We are building on this method by using even fewer measurements (interpolation) points and L1 optimization for reconstructing of inner products as well as classification of data. These methods are particularly important in reduced-order models and Galerkin projections of dynamical systems. Partnering the DEIM and L1 methods can potentially prove to be highly efficient computationally.
Selected Recent Publications
- S. Brunton, J. Proctor and J. N. Kutz, Discovering governing equations from data: sparse identification of nonlinear dynamical systems arXiv:1509.03580.
- I. Bright, G. Lin and J. N. Kutz, Classification of Spatio-Temporal Data via Asynchronous Sparse Sampling: Application to Flow Around a Cylinder, arXiv:1506.00661.
- S. Brunton, J. Proctor and J. N. Kutz, Compressive sampling and dynamic mode decomposition arXiv:1312.5186
- I. Bright, G. Lin and J. N. Kutz, Compressive sensing based machine learning strategy for characterizing the flow around a cylinder with limited pressure measurements, Physics of Fluids 25 (2013) 127102.
- J. Proctor, B. Brunton, S. Brunton and J. N. Kutz, Exploiting sparsity and equation-free architectures in complex systems, European Physics Journal Special Topics 223 (2014) 2665-2684.
- S. Brunton, J. Tu, I. Bright and J. N. Kutz, Compressive sensing and low-rank libraries for classification of bifurcation regimes in nonlinear dynamical systems, SIAM Journal of Applied Dynamical Systesm 13 (2014) 1716-1732.