Mathematical Methods

Developing Tools of Dynamical Systems for Broad Application

LOADING
  • Stacks Image 748

    Bifurcation Structure for Large Amplitude Water Waves

  • Stacks Image 750

    Compresssive Sensing Architecture with Point Measurements

  • Stacks Image 752

    Poincare Dynamics for a Dispersion Map in Nonlinear Schrodinger Equation

  • Stacks Image 754

    Multi-Scale Physics Modeling via Multi-Resolution Dynamic Mode Decomposition

  • Stacks Image 756

    Learned Libraries of Dynamic Modes in Flow Around a Cylinder

  • Stacks Image 758

    Data Reduction and Sparse Classification

  • Stacks Image 762

    Compressive Sensing for Classification and Reconstruction of Flow

  • Stacks Image 764

    Proper Orthogonal Decomposition Modes for Flow Around a Cylinder

  • Stacks Image 766

    Band Gap Structure in Nonlinear Schrodinger Equation with Periodic Potential

Mathematical Methods Development and Application

 

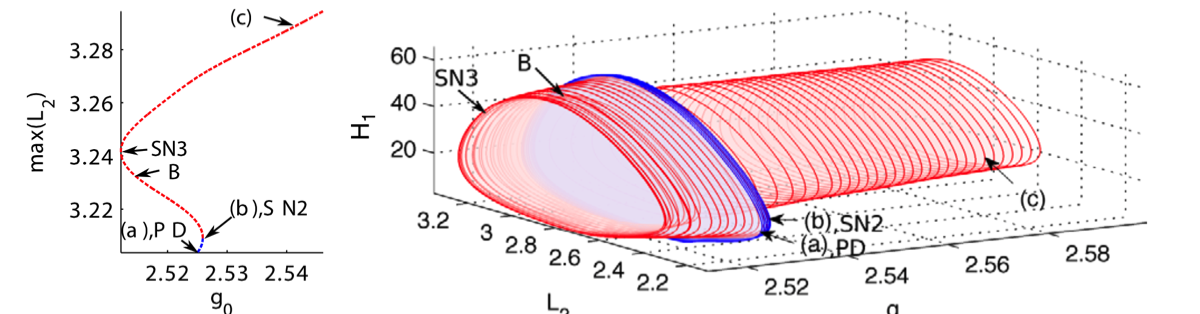
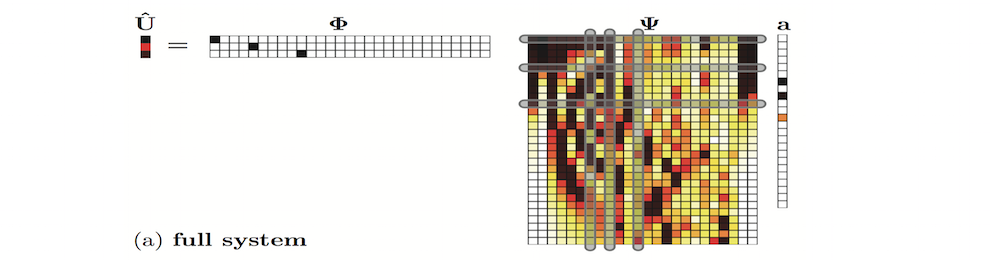
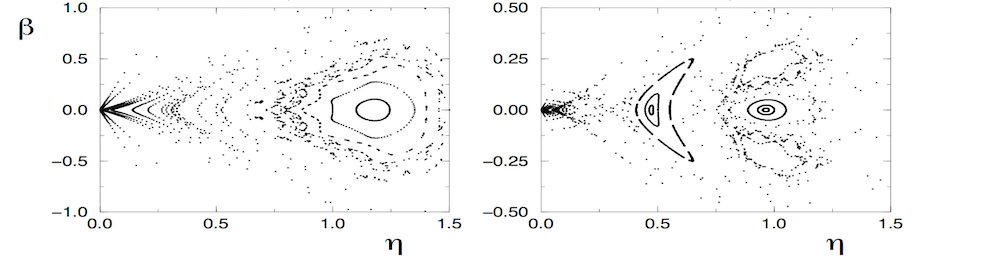
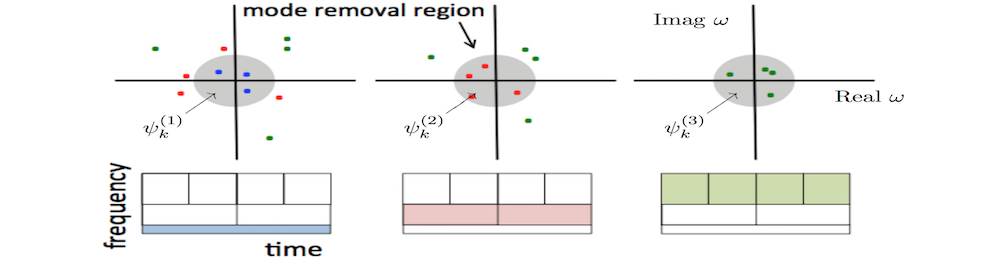
My background is in traditional applied mathematics methods from partial differential equations, dynamical systems, asymptotic and perturbation theory, and scientific computing. I originally did quite a bit of work on understanding the stability and bifurcation structure of localized solutions of nonlinear wave equations. Over the past 5 years, I have branched out into the data sciences and have developed a theoretical interest in applications of data methods to dynamical systems, including machine learning, compressive sensing, equation-free modeling and reduced-order modeling. Please click on the sublinks above to see specific areas of theoretical interest.
© 2015 kutz Contact Me