Equation-Free Modeling and Approximating Dynamics from Data
LOADING
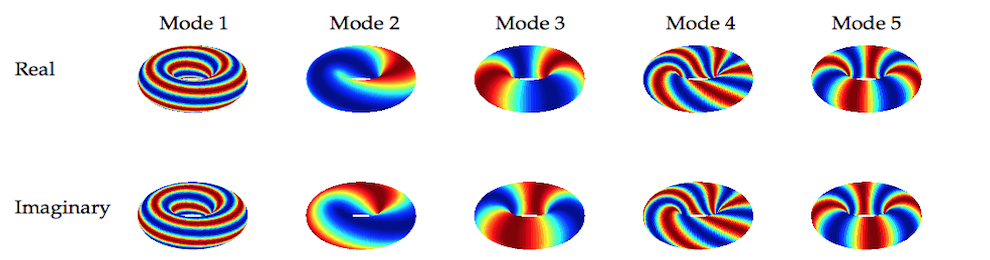
Connecting Dynamic Mode Decomposition and Koopman Theory
Introduced in 1931, the Koopman operator is a linear operator that completely describes an autonomous nonlinear dynamical system. This is accomplished by mapping a finite-dimensional nonlinear dynamical system to an infinite-dimensional linear system. Our work rests on the timely synthesis of the novel mathematical techniques of Koopman theory with Dynamic Mode Decomposition, thus framing the building blocks for rigorous data-driven, equation-free modeling strategies. This mathematical framework enables the synthesis of model reduction, sparse sampling, multi-resolution analysis and machine learning with the goal of (i) providing a rigorous mathematical connection with dynamical systems theory, and (ii) adaptively modeling and controlling complex, nonlinear processes.
Equation-Free Modeling of Multi-Scale Physics
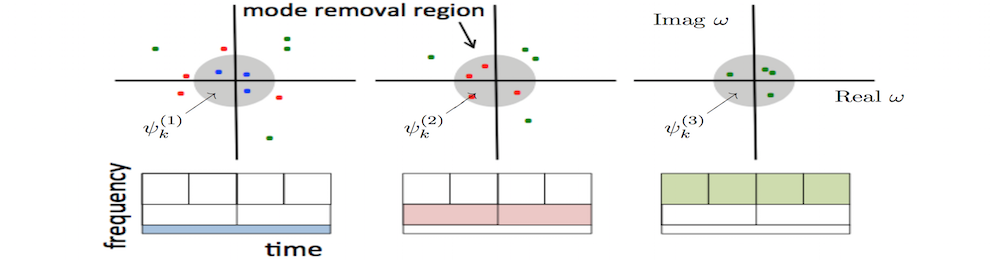
Many dynamical systems of interest are inherently multi-scale, in both space and time. Example of interest are found in complex fluids, neuroscience, climate, epidemiology, and network science. The spatial-temporal coherence of the associated data is not readily interrogated with the standard DMD or Koopman framework, motivating new techniques to incorporate multi-resolution analysis. The ability to investigate multi-scale phenomena will provide a key innovation to improve the value extracted from these data sets. The multi-resolution DMD (mrDMD) is inspired by the observation that the slow- and fast-modes can be separated for such applications as foreground/background subtraction in video feeds. The mrDMD recursively removes low-frequency, or slowly-varying, content from a given collection of snapshots. Typically, the number of snapshots are chosen so that the DMD modes provide an approximately full rank approximation of the dynamics observed. In mrDMD, the slowest modes are removed, and the domain is divided into two smaller time segments. DMD is once again performed on the smaller snapshot sequences. Again the slowest modes are removed and the algorithm is continued until a desired termination. Thus at each level, the slow dynamics are separated from the fast dynamics, giving a recursive scheme for multi-scale, equation-free modeling.
Equation-Free Control Protocols for Complex Systems
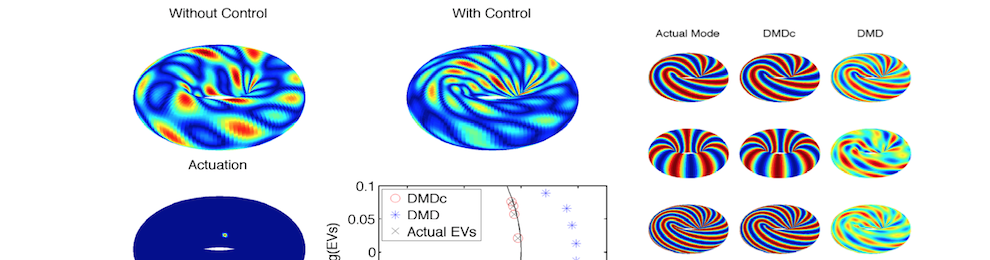
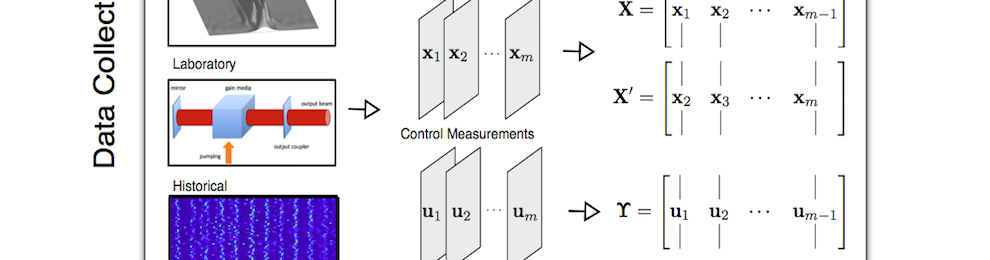
DMD has recently been extended to include the effect of control to extract low-order models from externally forced or controlled high-dimensional complex systems. In actuated systems, DMD is incapable of producing an input-output model, and the resulting modes are corrupted by the external forcing. The new method of dynamic mode decomposition with control (DMDc) provides the ability to disambiguate between the underlying dynamics and the effects of actuation, resulting in accurate input-output models. The DMDc method has been effective in a number of example systems, but innovations around multi-scale physics and sparsity remain open problems.
Selected Recent Publications
- J. N. Kutz, X. Fu and S. Brunton, Multi-Resolution Dynamic Mode Decomposition, arXiv:1506.00564.
- S. Brunton, J. Proctor and J. N. Kutz, Compressive sampling and dynamic mode decomposition arXiv:1312.5186
- J. Proctor, S. Brunton and J. N. Kutz, Dynamic mode decomposition with control, arXiv:1409.6358
- B. Brunton, L. Johnson, J. Ojemann and J. N. Kutz, Extracting spatial-temporal coherent patterns in large-scale neural recordings using dynamic mode decomposition arXiv:1409.5496
- J. Grosek and J. N. Kutz, Dynamic mode decomposition for real-time background/foreground separation in video, arXiv:1404.7592.