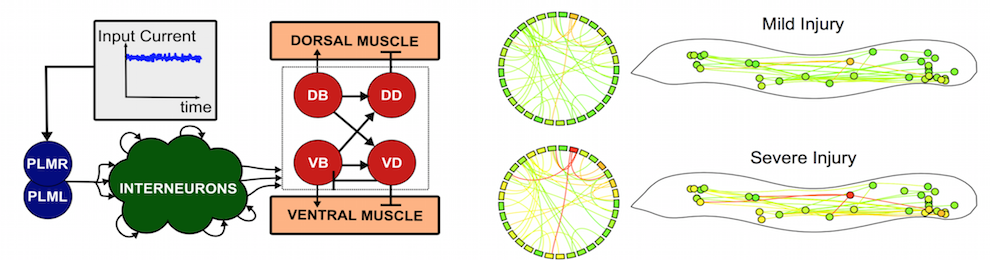
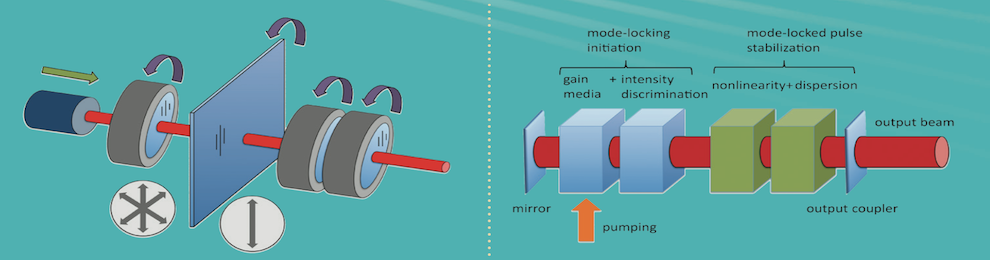
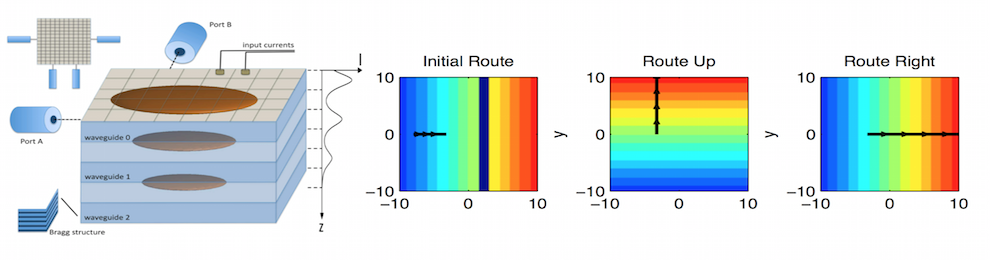
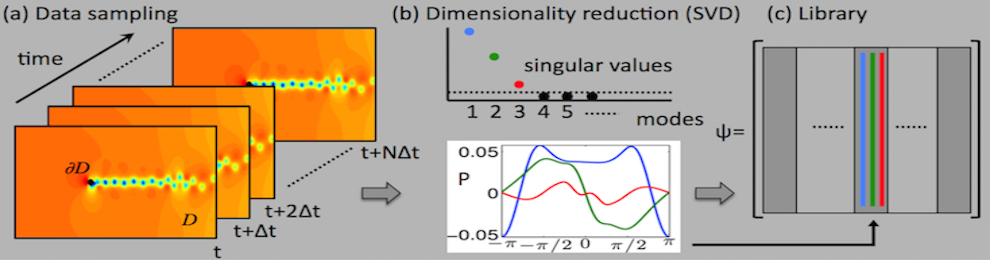
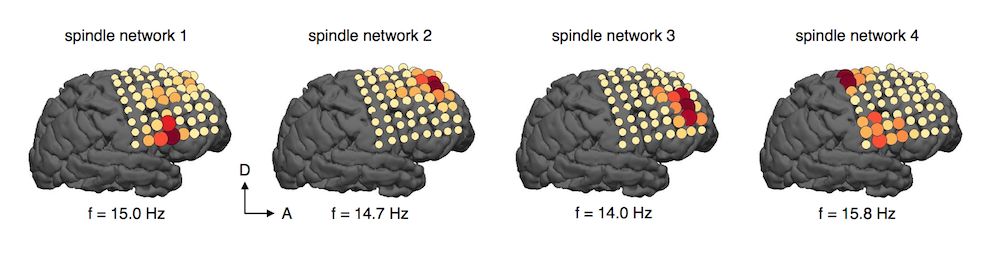
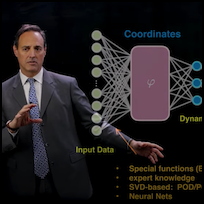
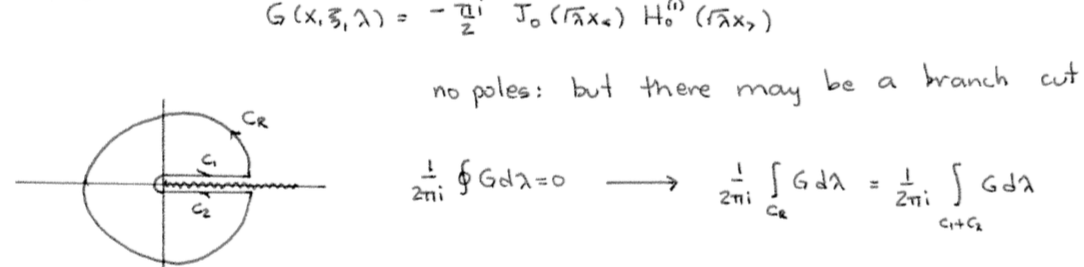Data-Driven Dynamical Systems
LOADING
QUANTA Magazine
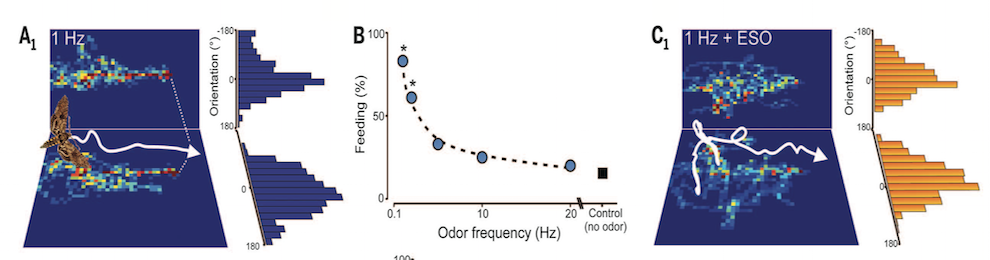
New AI Strategy Mimics How Brains Learn to Smell
- Feature article on Delahunt & Kutz work: READ
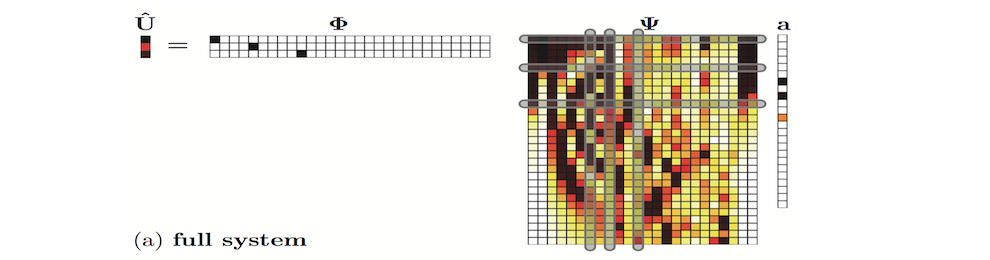
- B. Lusch, J. N. Kutz and S. L. Brunton, Deep learning for universal linear embeddings of nonlinear dynamics, Nature Communications 4950 (2018).
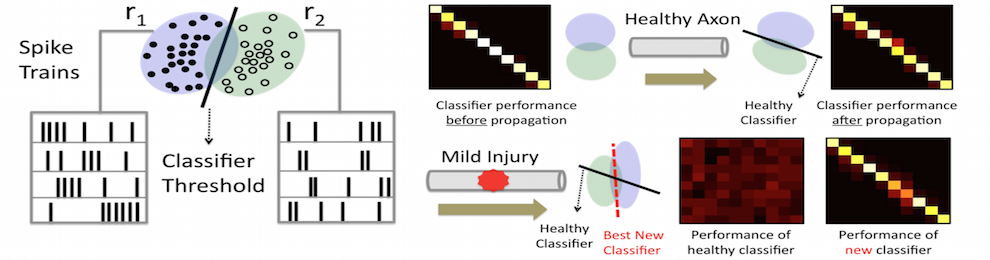
- C. Delahunt and J. N. Kutz, Insect cyborgs: Biological feature generators improve machine learning accuracy on limited data, arxiv:1808.08124 (2018).
- C. Delahunt and J. N. Kutz, Putting a bug in ML: the moth olfactory network learns to read MNIST, arxiv:1802.05405 (2018).
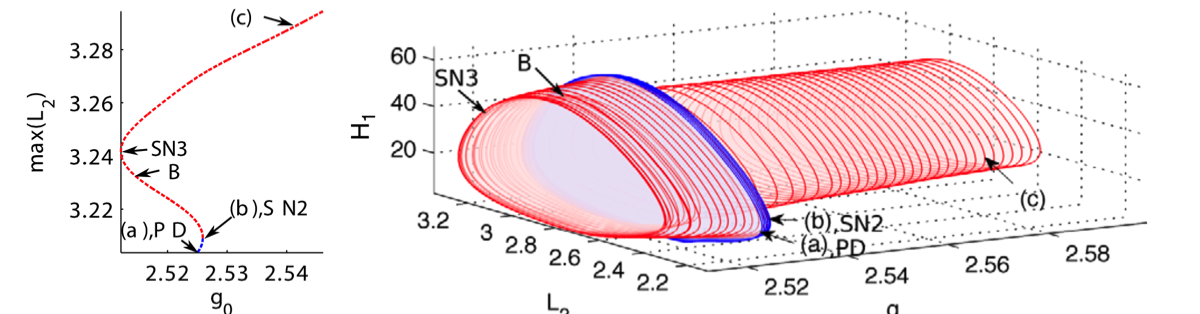
- S. Rudy, J. N. Kutz and S. L. Brunton, Deep learning of dynamics and signal-noise decomposition with time-stepping constraints, arxiv:1808.02578 (2018).
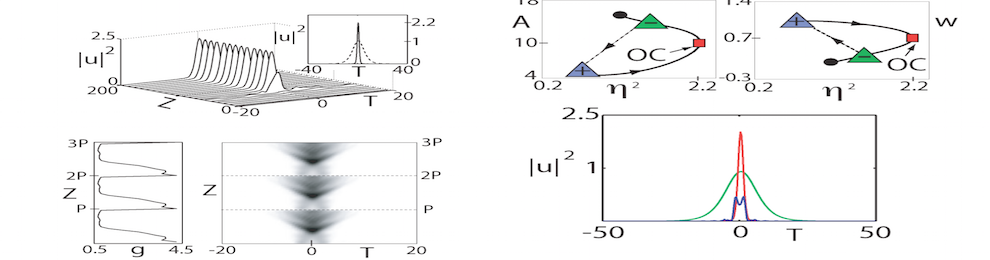
- T. Baumeister, S. L. Brunton and J. N. Kutz, Deep learning and model predictive control for self-tuning mode-locked lasers, J. Opt. Soc. Am. B 35, 617-626 (2018).