Sensors

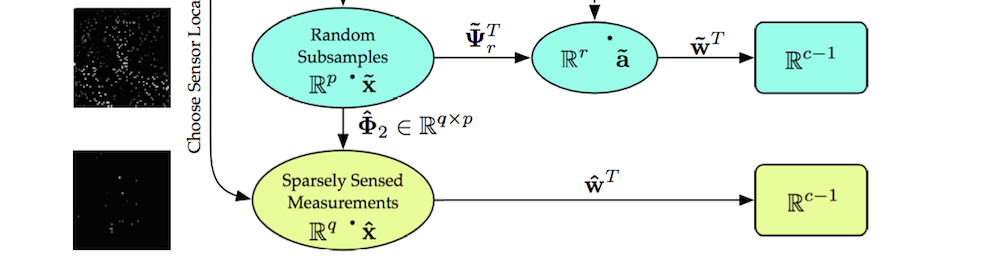
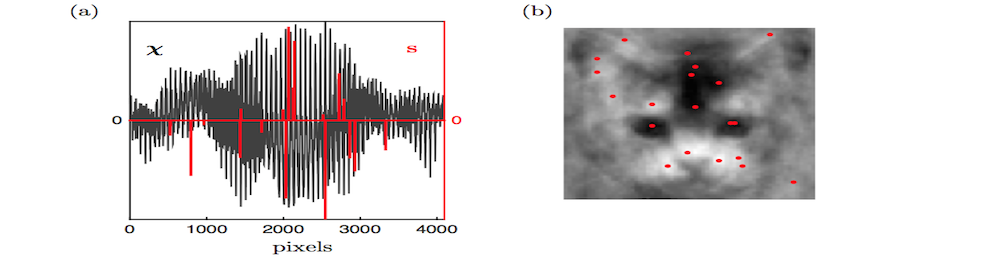
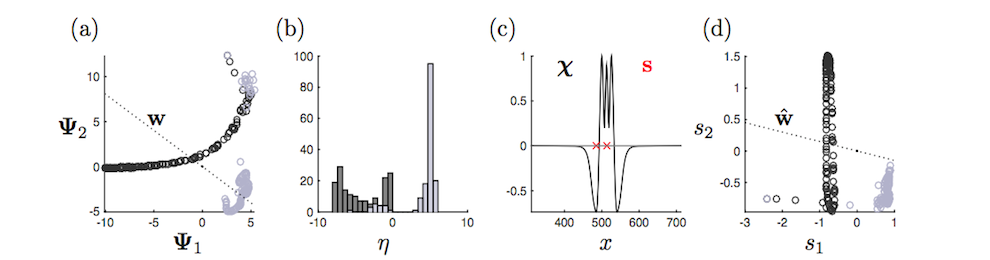
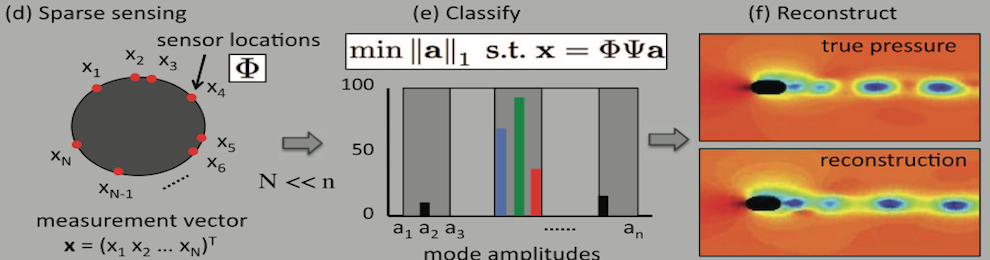
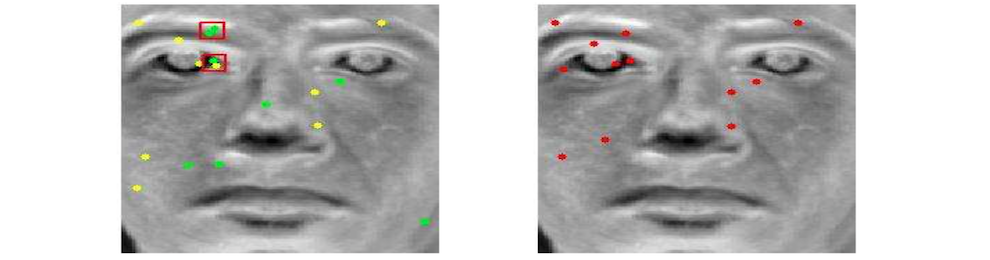
Choosing a limited set of sensor locations to characterize or classify a high-dimensional system is an important challenge in engineering design. Traditionally, optimizing the sensor locations involves a brute-force, combinatorial search, which is NP-hard and is computationally intractable for even moderately large problems. Using recent advances in sparsity-promoting techniques, we have developed a novel algorithm to solve this sparse sensor placement optimization for classification (SSPOC) that exploits low-dimensional structure exhibited by many high-dimensional systems. Our approach is inspired by compressed sensing, a framework that reconstructs data from few measurements. If only classification is required, reconstruction can be circumvented and the measurements needed are orders-of-magnitude fewer still. Our algorithm solves an L1 minimization to find the fewest nonzero entries of the full measurement vector that exactly reconstruct the discriminant vector in feature space; these entries represent sensor locations that best inform the decision task. Once training identifies sensor locations, data taken at these locations form a low-dimensional measurement space, and we perform computationally efficient classification with accuracy approaching that of classification using full state data. The algorithm also works when trained on heavily subsampled data, eliminating the need for unrealistic full-state training data.

From a dynamical systems perspective, we have been developing innovations around the DEIM (Discrete Empirical Interpolation) method and its application to sensors. The discrete sampling points given by the DEIM to evaluate the nonlinearity get a new interpretation in our work. Specifically, we show them to be the effective locations for placing sensors in a nonlinear dynamical system in order to (i) determine the dynamic regime of the system, (ii) reconstruct the current state of the system, and (iii) produce a POD-Galerkin prediction (nonlinear model reduction) of the future state of the system. Such tasks are accomplished by using ideas of sparse representation and compressive sensing. In particular, the theory of compressive sensing shows that a small number of measurements are sufficient to perform a reconstruction provided there exists a sparse representation (or basis) of the data. In our case, the sparse basis is generated from a library learning procedure of a nonlinear dynamical system that exhibits low-rank dynamics. More than that, however, we also build libraries of the nonlinearities, thus pre-computing the low-dimensional structures observed in the different dynamical states of the nonlinear dynamical system. This allows for more robust dynamical classification as well as allowing easy evaluation of the nonlinear terms through the DEIM. The combination of library building, compressive sensing and the DEIM is demonstrated to be a highly effective and intuitively appealing methodology for scientific computing applications. It further highlights the need in modern scientific computing of nonlinear dynamical systems to integrate a variety of data-driven modeling strategies, many of which are being developed under the aegis of dimensionality reduction, in order to most efficiently simulate large-scale systems.

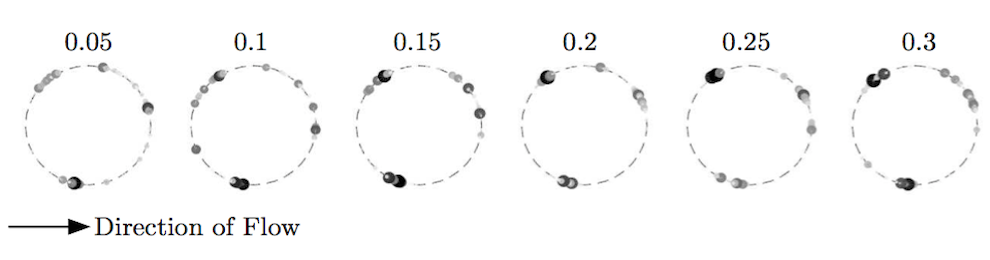
Our recent research has led us to conjecture that a principled approach to sensing in complex spatio-temporal systems will allow us to probe the latent, low-dimensional structure of dynamic activity relating to the fundamental quantities of interest. A direct implication of such a data-driven modeling strategy is that we can gain traction on prediction, state-estimation and control of the complex system. To this end, we have demonstrated that asynchronous sparse measurements in both time and space allows for a robust method, i.e. a spatio-temporal compressive sensing method, for classifying the dynamical behavior of a given system. Once classified, it can be used for full state reconstruction and/or future state prediction of the full spatio-temporal system, extending previous works which only reconstructed single time snapshots of the data.