Reduced-Order Modeling

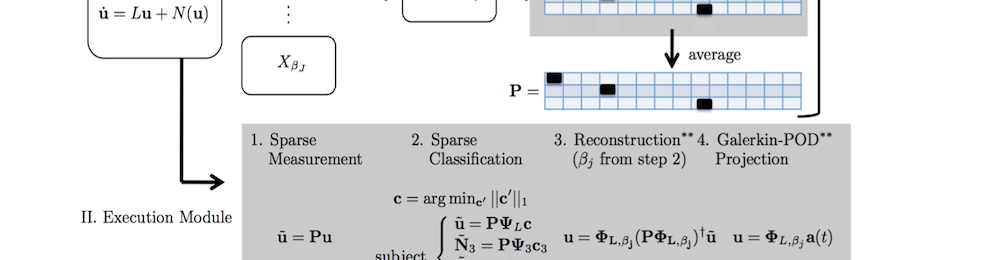
Efficiently managing the computation of the nonlinearity (inner products) in dimensionality reduction schemes is of paramount importance. This was recognized early on in the reduced order modeling community, and a variety of techniques where proposed to accomplish the task. Among the first methods used was the technique of Everson and Sirovich developed for gappy data. In their sparse sampling scheme, random measurements were used to perform reconstruction tasks of inner products. Willcox and Karniadakis built on these ideas by advocating principled approaches for selecting sampling locations for Gappy POD. The EIM, and the variant of this technique known as the DEIM method, was also developed for the purpose of efficiently managing the computation of the nonlinearity. The discrete sampling points given by the DEIM to evaluate the nonlinearity gets a new interpretation in our current work. Specifically, we show them to be the effective locations for placing sensors in the nonlinear dynamical system in order to (i) determine the dynamic regime of the system, (ii) reconstruct the current state of the system, and (iii) produce a POD-Galerkin prediction (nonlinear model reduction) of the future state of the system. We are continuing to develop even better interpolation strategies that require fewer measurements and near-optimal placement.

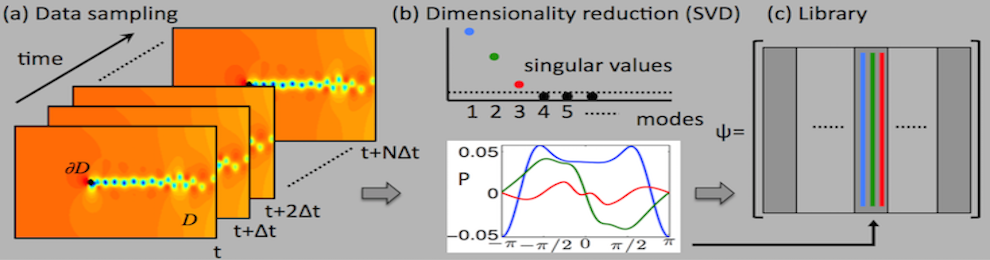
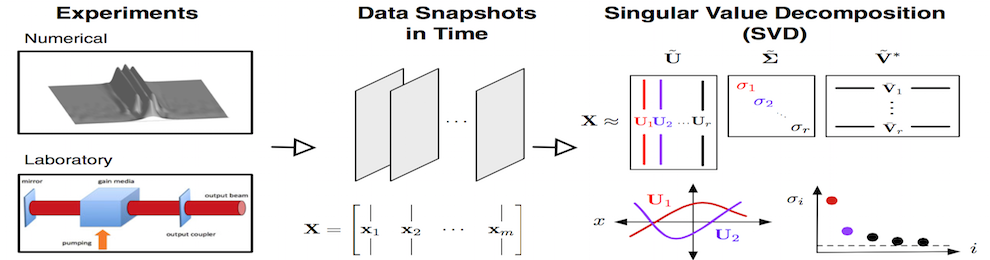
Although a variety of dimensionality-reduction techniques exist, the ROM methodology is often based upon the proper orthogonal decomposition (POD). The POD method is ubiquitous in the dimensionality reduction of physical systems. It is alternatively referred to as principal components analysis (PCA), the Karhunen-Loeve (KL) decomposition, empirical orthogonal functions (EOF), or the Hotelling transform. Snapshots (measurements) of many nonlinear dynamical system often exhibit low-dimensional phenomena, so that the majority of variance/energy is contained in a few modes computed from a singular value decomposition (SVD). For such a case, the POD basis is typically truncated at a pre-determined cut-off value, such as when the modal basis contain 99% of the variance, so that only the first r-modes (r-rank truncation) are kept. These modes are used to build libraries of dynamical behavior for parametric systems. The SVD acts as a filter, and often the truncated modes correspond to random fluctuations and disturbances. If the data considered are generated by a dynamical system (nonlinear system of ordinary differential equations of order n), it is then possible to substitute the truncated POD expansion into the governing equation and obtain Galerkin projected dynamics on the rank-r basis modes, i.e. our reduced-order model. The library building procedure is done off-line and is used for both storing low-rank modes and inner products evaluations of the nonlinear terms. These libraries can be recalled in an on-line fashion for efficient computation.