Machine Learning + Dynamics

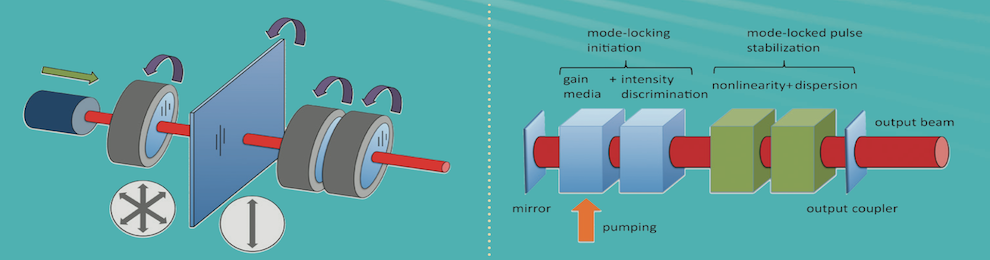
Data-driven discovery methods are having a profound impact across the physical, engineering and biological sciences. The goal of these emerging methods is to mine big data content for low-dimensional patterns of activity and/or clustering of behaviors. Such pattern recognition algorithms, typically falling under the aegis of machine learning methods, are then capitalized on for control, optimization or characterization of the system under consideration. The success of these methods, such as self-driving automobiles, have brought society to the brink of a technology revolution. As we have recently shown, optical systems are far less complex than self-driving algorithms, thus suggesting that self-tuning methods should be easily implementable in the much more limited parameter space afforded by, for example, mode-locked fiber lasers and/or metamaterial antennas.

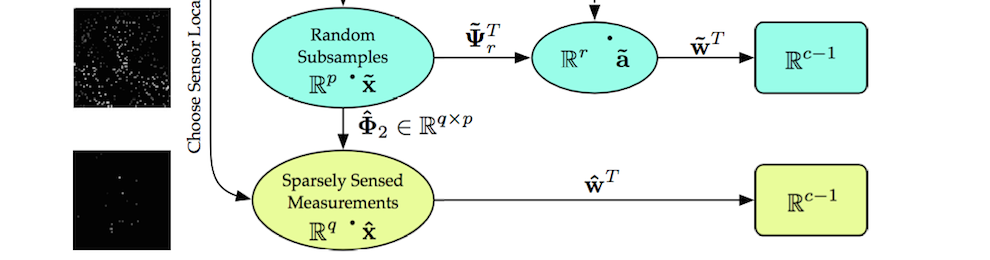
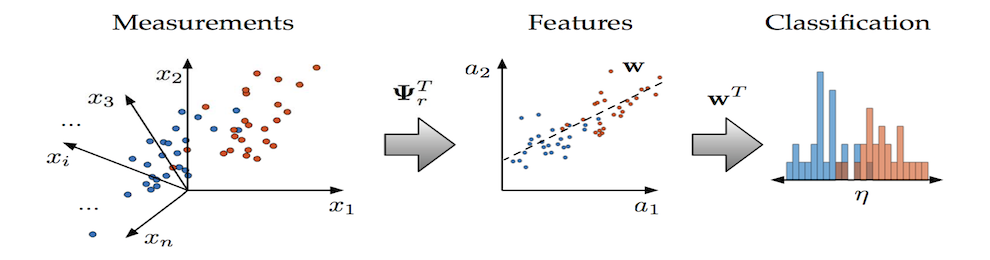
Machine learning is based upon algorithms. These algorithms aim to learn and clusters patterns typically in a low-dimensional spaces. The algorithmic procedure used for dimensionally reducing, classifying and reconstruction relies first on building a library of modes acquired, in an offline manner, by low-rank projections (SVD) of data. The
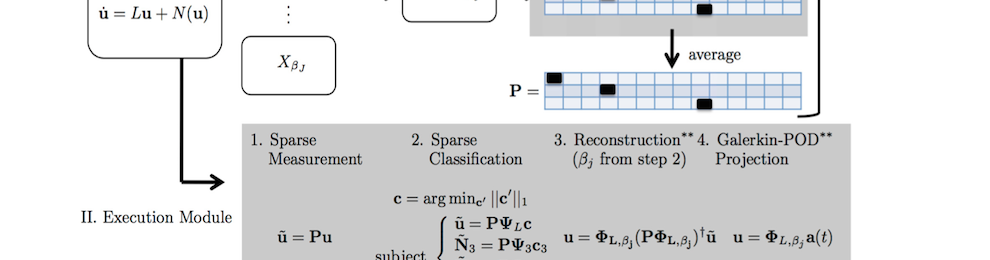
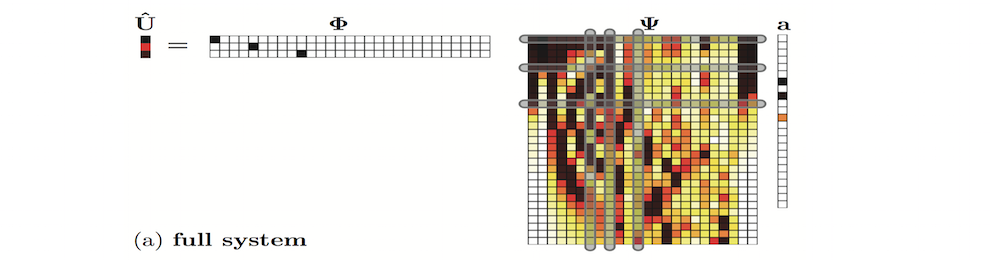
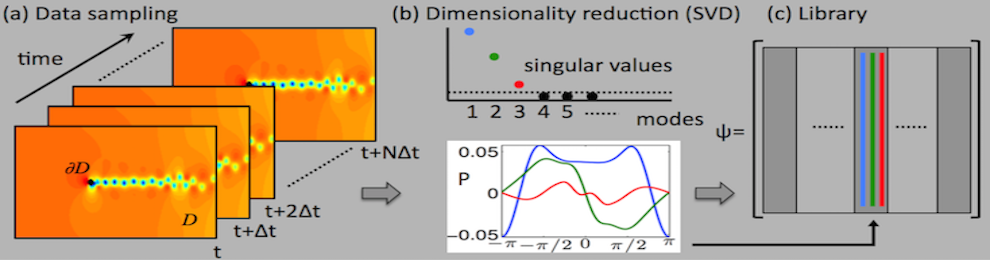
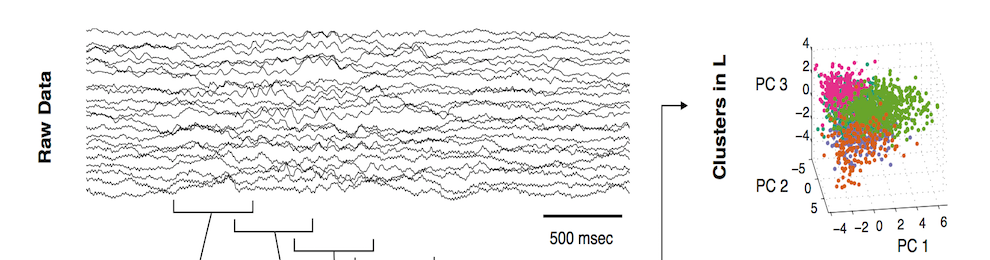
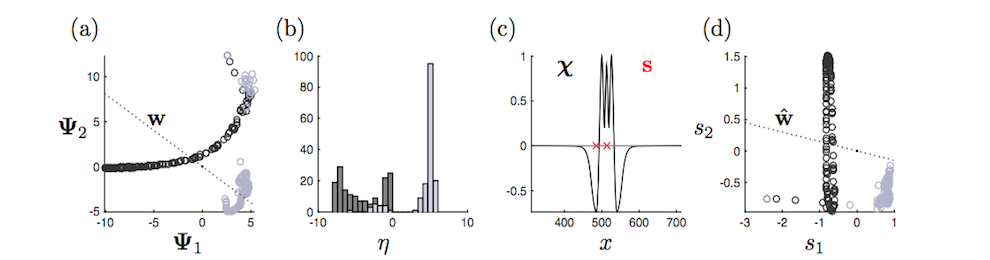
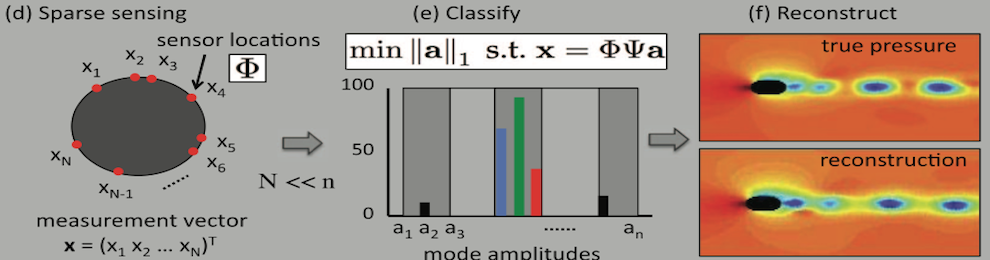
machine learning portion of the algorithm thus relies on (a) data sampling of the full, highly-resolved complex system which is then (b) dimensionally reduced through SVD/POD/PCA and (c) stored in a libraries (matrices) matrix. Once constructed, (d) sparse sensing at a limited number of locations can be used to (e) classify the dynamical regime by solving an L1 convex optimization problem. The L1 norm promotes sparsity and allows the classification to identify the current relevant dynamic modes from the learned libraries. Further, the a reconstruction of the data can be then made from limited measurements and the correct library modes. Such a framework is ideal for high-dimensional dynamical systems where low-dimensional patterns of activity dominate many meaningful behaviors.