Transfer
Function
Frequency
Response
Dr. Layer 1.0 Exercise 5 - Damping Effects
Background
In a homogeneous linear elastic material, stress waves travel indefinitely without change in amplitude. This type of behavior can not occur, however, in real conditions. The amplitudes of stress waves in real materials, such as those that comprise the earth, attenuate with distance. This attenuation can be attributed to two sources of energy dissipation, one which involves the material through which the waves travel and the other the geometry of the wave propagation problem. In this particular exercise we will concentrate on the first form of dissipation of energy.
In real materials, part of the elastic energy of a traveling wave is always converted to heat. The conversion is accompanied by a decrease in the amplitude of the wave. For specific soils and structures, however, the operative mechanisms by which the energy is dissipated are not understood sufficiently to allow them to be explicitly modeled. As a result, the effects of the various energy loss mechanisms are usually lumped together and represented by some convenient damping mechanism. The most commonly used mechanism for representing energy dissipation is viscous damping which assumes the existence of dissipative forces that are a function of particle velocity. For most soils and structures, however, energy is dissipated hysteretically. That is by yielding or plastic straining of the material.
The type of damping described above is called material damping, because the material absorbs the energy of travel during wave propagation. The reduction in energy per unit volume causes the amplitude of the wave to decrease with increasing displacement. However, a different type of damping (reduction in energy per unit volume) can be observed which occurs when the energy of the wave is spread over a very large area and thus it dies off quickly. This type of damping is usually referred as radiation damping.
BACK TO TOP
Objective
In the examples that will comprise this section the attenuation of the wave amplitude will be investigated by: a)considering a viscous mechanism, and b)by considering the nonlinear non-elastic behavior of soils.Things to Do
a) Viscous Damping- Open the Dr. Layer program. Select "all layers" and assign
them a "very slow" wave speed. By default the no-damping
option is selected.
- Choose a pulse load and using the sliders adjust its amplitude and
frequency to a high value (80% of max).
- By default DrLayer starts with a single plotting window at the bottom
of the layer. Using the plot box buttom,
,
add two additional plot-boxes at the top and middle of the layer as
shown in Figure 1.
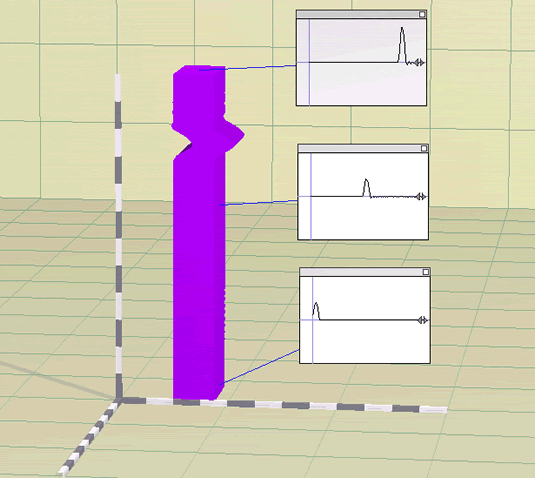
Figure 1 - Viscous damping in a single layer soil profile
- Starting with the set up described above, press the time increment
buttom,
to set up the wave motion. Note that the wave travels along the layer
without changes and its reflected at the free end.
- Change the damping coefficient of all the layers to "high"
by using the "damping" drop-down menu on the top of
your screen, and reset the system by pressing the
buttom. Restart the motion by pressing the time increment buttom and
observe the changes in the wave as it travels along the layer.
- Answer the following questions: a)Is the wave motion amplitude affected?? b)Is the wave speed affected??; c)What can you say about the energy originally given to the system? Is it lost?? How??
b) Hysteretic Damping
- Restart
the DrLayer program. Select the bottom eight layers and assign them
a "very fast" wave speed. This material will be referred
to as Material 1. Select the top four layers and assign them a "slow"
wave speed. This material will be referred to as Material 2.
- Choose
a pulse load and adjust its frequency to a high value (~80% max) by
using the frequency slider on the top of your screen.
- Select a bilinear material model with low yield stress using the "Material
Models..." option available in the "options"
drop down menu.
- To visualize the stress-strain soil response add stress-strain plot
boxes at convenient places using the
buttom while pressing the Ctrl+Shift keys. For this particular problem
we suggest to use two plot boxes located close to the material interface,
Figure 2.
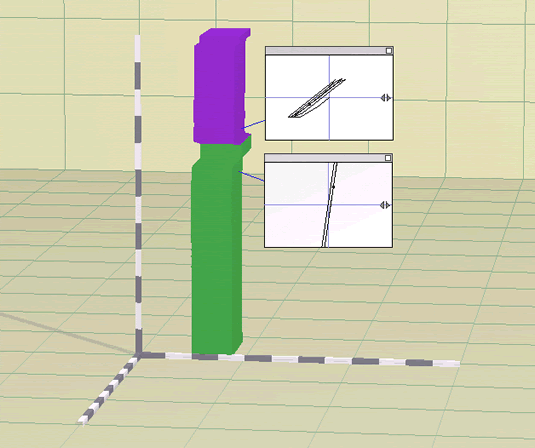
Figure 2 - Material damping in a two layer soil profile
- Starting with the set up described above, press the time increment
buttom to set up the wave motion. Note that the wave travels along material
1 without noticeable changes. At the interface, part of the energy carried
by the wave is transferred to material 2 and part of it is reflected.
Note that, as result of the interaction at the interface, permanent
deformations are concentrated close to the interface. Consequently,
the stress-strain curves at these points do not follow a straight line.
At the top and bottom of the layer a similar behavior is also observed.
- As time goes on the wave will be transmitted and reflected multiple
times at the interface. During each interaction additional plastic deformations
may occur.
- Answer the following questions:
a) Is the initial wave energy affected during the motion??
b) Where does the energy go??
c) Can you imagine a way to estimate the amount of energy lost?
d) Can you think of a similar mechanism in mechanics? Give a couple of examples.
BACK TO TOP
Observation
Damping can be thought of as some form of resistance to impeding motion. Friction readily comes to mind and helps as an analogy for thinking about damping. Due to friction part of the energy is transformed to heat or is dissipated in the form or irrecoverable or plastic deformations.On Your Own
Viscous Damping- Use different material stiffness and repeat the exercise.
- Use different damping values and repeat the analysis.
- Repeat the process with elastic materials. Do you observe the attenuation of waves??
- Use different material stiffness and different impedance ratios.
- Use different yield stresses and investigate the effect of hardening
in the attenuation of waves.
BACK TO TOP
Last
Updated:
12/27/00
Contact us at: parduino@u.washington.edu