mmf.math.linalg.cholesky.gmw81

gmchol(A[, test])	Return (L, e): the Gill-Murray generalized Cholesky
colmod(A)	Modified Cholesky factorization
mchol2(A)	Based on the MATLAB code

These are a collection of codes based on the [GMW81] algorithm.

Comments

colmod() :

Seems to work well and is quite efficient as it has been vectorized, but not quite as good as gmw(). Use this for now.

gmw() :

Seems to work well, but returns an explicit pivoting matrix and is very slow as it uses loops.

gmchol() :

Fast (uses weave) but very bad for large matrices because it uses no pivoting.

mmf.math.linalg.cholesky.gmw81.gmchol(A, test=False)

Return (L, e): the Gill-Murray generalized Cholesky decomposition of M = A + diag(e) = dot(L, L.T) where

1. M is safely symmetric positive definite (SPD) and well conditioned.
2. e is small (zero if A is already SPD and not much larger than the most negative eigenvalue of A)

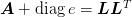
Parameters :

A : array

Must be a non-singular and symmetric matrix

test : bool

If True, use the directly translated iterative code for testing.

Returns :

L : 2d array

Lower triangular Cholesky factor.

e : 1d array

Diagonals of correction matrix E.

Notes

Translated from the following Gauss code of J. Gill::

****************************************************************/ * This is the Gill/Murray cholesky routine. Reference: / * */ * Gill, Jeff and Gary King. ``What to do When Your Hessian */ * is Not Invertible: Alternatives to Model Respecification */ * in Nonlinear Estimation,’’ Sociological Methods and */ * Research, Vol. 32, No. 1 (2004): Pp. 54–87. */ * */ * Abstract */ * */ * What should a researcher do when statistical analysis */ * software terminates before completion with a message that */ * the Hessian is not invertable? The standard textbook advice */ * is to respecify the model, but this is another way of saying */ * that the researcher should change the question being asked. */ * Obviously, however, computer programs should not be in the */ * business of deciding what questions are worthy of */ * study. Although noninvertable Hessians are sometimes signals */ * of poorly posed questions, nonsensical models, or */ * inappropriate estimators, they also frequently occur when */ * information about the quantities of interest exists in the */ * data, through the likelihood function. We explain the */ * problem in some detail and lay out two preliminary proposals */ * for ways of dealing with noninvertable Hessians without */ * changing the question asked. */ ***************************************************************/

proc gmchol(A);

/* calculates the Gill-Murray generalized choleski decomposition / / input matrix A must be non-singular and symmetric / / Author: Jeff Gill. Part of the Hessian Project. */ local i,j,k,n,sum,R,theta_j,norm_A,phi_j,delta,xi_j,gamm,E,beta_j; n = rows(A); R = eye(n); E = zeros(n,n); norm_A = maxc(sumc(abs(A))); gamm = maxc(abs(diag(A))); delta = maxc(maxc(__macheps*norm_A~__macheps)); for j (1, n, 1);

theta_j = 0; for i (1, n, 1);

sum = 0; for k (1, (i-1), 1);

sum = sum + R[k,i]*R[k,j];

endfor; R[i,j] = (A[i,j] - sum)/R[i,i]; if (A[i,j] -sum) > theta_j;

theta_j = A[i,j] - sum;

endif; if i > j;

R[i,j] = 0;

endif;

endfor; sum = 0; for k (1, (j-1), 1);

sum = sum + R[k,j]^2;

endfor; phi_j = A[j,j] - sum; if (j+1) <= n;

xi_j = maxc(abs(A[(j+1):n,j]));

else;

xi_j = maxc(abs(A[n,j]));

endif; beta_j = sqrt(maxc(maxc(gamm~(xi_j/n)~__macheps))); if delta >= maxc(abs(phi_j)~((theta_j^2)/(beta_j^2)));

E[j,j] = delta - phi_j;

elseif abs(phi_j) >= maxc(((delta^2)/(beta_j^2))~delta);

E[j,j] = abs(phi_j) - phi_j;

elseif ((theta_j^2)/(beta_j^2)) >= maxc(delta~abs(phi_j));

E[j,j] = ((theta_j^2)/(beta_j^2)) - phi_j;

endif; R[j,j] = sqrt(A[j,j] - sum + E[j,j]);

endfor; retp(R’R);

endp;

Examples

>>> np.random.seed(3)
>>> A = np.random.rand(100,100)*2 - 1
>>> A = A + A.T
>>> L, e = gmchol(A, test=True)
>>> np.allclose(np.dot(L,L.T), (A + np.diag(e)))
True
>>> -e.max()/np.linalg.eigvalsh(A).min() < 1000
True

>>> A2 =  np.array([[-0.451, -0.041, 0.124],
...                 [-0.041, -0.265, 0.061],
...                 [ 0.124, 0.061, -0.517]])
>>> L, e = gmchol(A2, test=True)
>>> e.max()/np.linalg.eigvalsh(A).min()

mmf.math.linalg.cholesky.gmw81.colmod(A)

Modified Cholesky factorization

R = cholmod(A) returns the upper Cholesky factor of A (same as chol) if A is (sufficiently) positive definite, and otherwise returns a modified factor R with diagonal entries >= sqrt(delta) and offdiagonal entries <= beta in absolute value, where delta and beta are defined in terms of size of diagonal and offdiagonal entries of A and the machine precision; see below. The idea is to ensure that E = A - R’*R is reasonably small if A is not too far from being indefinite. If A is sparse, so is R. The output parameter indef is set to 0 if `A is sufficiently positive definite and to 1 if the factorization is modified.

The point of modified Cholesky is to avoid computing eigenvalues, but for dense matrices, MODCHOL takes longer than calling the built-in EIG, because of the cost of interpreting the code, even though it only has one loop and uses vector operations.

reference: Nocedal and Wright, Algorithm 3.4 and subsequent discussion (not Algorithm 3.5, which is more complicated) original algorithm is due to Gill and Murray, 1974 written by M. Overton, overton@cs.nyu.edu, last modified Feb 2005

convenient to work with A = LDL’ where D is diagonal, L is unit lower triangular, and so R = (LD^(1/2))’

Notes

This is based on the following MATLAB code from Michael L. Overton: http://cs.nyu.edu/overton/g22_opt/codes/cholmod.m

function [R, indef, E] = cholmod(A)
if sum(sum(abs(A-A'))) > 0
    error('A is not symmetric')
end

% set parameters governing bounds on L and D (eps is machine epsilon)

n = length(A);
diagA = diag(A);
gamma = max(abs(diagA));             % max diagonal entry
xi = max(max(abs(A - diag(diagA))));  % max offidagonal entry
delta = eps*(max([gamma+xi, 1]));
beta = sqrt(max([gamma, xi/n, eps]));
indef = 0;

% initialize d and L

d = zeros(n,1);
if issparse(A)
    L = speye(n);  % sparse identity
else
    L = eye(n);
end

% there are no inner for loops, everything implemented with
% vector operations for a reasonable level of efficiency

for j = 1:n
    K = 1:j-1;  % column index: all columns to left of diagonal
                % d(K) doesn't work in case K is empty
    djtemp = A(j,j) - L(j,K)*(d(K,1).*L(j,K)');   % C(j,j) in book
    if j < n
        I = j+1:n;  % row index: all rows below diagonal
        Ccol = A(I,j) - L(I,K)*(d(K,1).*L(j,K)');  % C(I,j) in book
        theta = max(abs(Ccol));
        % guarantees d(j) not too small and L(I,j) not too big
        % in sufficiently positive definite case, d(j) = djtemp
        d(j) = max([abs(djtemp), (theta/beta)^2, delta]);
        L(I,j) = Ccol/d(j);
    else
        d(j) = max([abs(djtemp), delta]);
    end
    if d(j) > djtemp  % A was not sufficiently positive definite
        indef = 1;
    end
end
% convert to usual output format: replace L by L*sqrt(D) and transpose
for j=1:n
    L(:,j) = L(:,j)*sqrt(d(j));   % L = L*diag(sqrt(d)) bad in sparse case
end;
R = L';
if nargout == 3
    E = A - R'*R;
end

Examples

>>> np.random.seed(3)
>>> A = np.random.rand(100,100)*2-1
>>> A = A + A.T
>>> L, e = colmod(A)
>>> np.allclose(np.dot(L, L.T) - np.diag(e), A)
True
>>> 0 < np.linalg.eigvalsh(A + np.diag(e)).min()
True
>>> -e.max()/np.linalg.eigvalsh(A).min() < 1000
True

mmf.math.linalg.cholesky.gmw81.mchol2(A)

Based on the MATLAB code

by Brian Borchers and Michael Zibulevsky:

%
%  [L,D,E,pneg]=mchol2(G)
%
%  Given a symmetric matrix G, find a matrix E of "small" norm and c
%  L, and D such that  G+E is Positive Definite, and
%
%      G+E = L*D*L'
%
%  Also, calculate a direction pneg, such that if G is not PSD, then
%
%      pneg'*G*pneg < 0
%
%  Reference: Gill, Murray, and Wright, "Practical Optimization", p111.
%  Author:        Brian Borchers (borchers@nmt.edu)
%  Modification:  Michael Zibulevsky   (mzib@ee.technion.ac.il)
%
function [L,D,E,pneg]=mcholmz3(G)
%
%  n gives the size of the matrix.
%
n=size(G,1);
%
%  gamma, zi, nu, and beta2 are quantities used by the algorithm.
%
gamma=max(diag(G));
zi=max(max(G-diag(diag(G))));
nu=max([1,sqrt(n^2-1)]);
beta2=max([gamma, zi/nu, 1.0E-15]);

C=diag(diag(G));

L=zeros(n);
D=zeros(n,1);  %  use vestors as diagonal matrices
E=zeros(n,1);  %%****************** **************

%
%  Loop through, calculating column j of L for j=1:n
%

for j=1:n,

    bb=[1:j-1];
    ee=[j+1:n];

    if (j > 1),
        L(j,bb)=C(j,bb)./D(bb)';     %  Calculate the jth row of L.
    end;

    if (j >= 2)
        if (j < n),
            C(ee,j)=G(ee,j)- C(ee,bb)*L(j,bb)';    %  Update the jth column of C.
        end;
    else
        C(ee,j)=G(ee,j);
    end;

    %%%%     Update theta.

    if (j == n)
        theta(j)=0;
    else
        theta(j)=max(abs(C(ee,j)));
    end;

    %%%%%  Update D

    D(j)=max([eps,abs(C(j,j)),theta(j)^2/beta2]');

    %%%%%%  Update E.

    E(j)=D(j)-C(j,j);

    %%%%%%%  Update C again...

    %for i=j+1:n,
    %    C(i,i)=C(i,i)-C(i,j)^2/D(j,j);
    %end;

    ind=[j*(n+1)+1 : n+1 : n*n]';
    C(ind)=C(ind)-(1/D(j))*C(ee,j).^2;

end;

%
% Put 1's on the diagonal of L
%
%for j=1:n,
%    L(j,j)=1;
%end;

ind=[1 : n+1 : n*n]';
L(ind)=1;

%
%  if needed, finded a descent direction.
%
if (nargout == 4)
    [m,col]=min(diag(C));
    rhs=zeros(n,1);
    rhs(col)=1;
    pneg=L'

hs;

end;

return

%%%%%%%%%%%%%%%%%%%%%% Test %%%%%%%%%%%%%

n=3; G=rand(n);G=G+G’;eigG=eig(G), [L,D,E,pneg]=mchol(G) [L1,D1,E1,pneg1]=mcholmz1(G); LL=L-L1, DD=D-D1, EE=E-E1, pp=pneg-pneg1

n=3; G=rand(n);G=G+G’;eigG=eig(G), [L,D,E,pneg]=mchol(G) [L2,D2,E2,pneg2]=mcholmz2(G); LL=L-L2, DD=D-diag(D2), EE=E-diag(E2), pp=pneg-pneg2