Navigation

Previous topic

mmf.math.linalg.cholesky.gmw81

Next topic

mmf.math.linalg.pardiso

This Page

mmf.math.linalg.cholesky.se99

se99(A) A revised modified Cholesky factorisation algorithm.
eschol(A) Here is a MATLAB translation of the same code:
modchol(A)

Notes
air_modchol(A) This is based on the following c code from the `AIR project

These are a collection of codes based on the [ES99] algorithm.

mmf.math.linalg.cholesky.se99.se99(A)[source]

A revised modified Cholesky factorisation algorithm.

Schnabel, R. B. and Eskow, E. 1999, A revised modifed cholesky factorisation algorithm. SIAM J. Optim. 9, 1135-1148.

Notes

The invariant here is that at stage j:

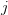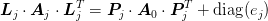
\mat{L}_{j}\cdot\mat{A}_{j}\cdot\mat{L}_{j}^{T} = \mat{P}_{j}\cdot\mat{A}_{0}\cdot\mat{P}_{j}^{T} + \diag(e_{j})

with the final stage 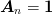\mat{A}_{n} = \mat{1}. We store 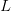L in the lower portion of A.

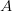mmf.math.linalg.cholesky.se99.eschol(A)[source]

Here is a MATLAB translation of the same code:: % /* % ** By Jeff Gill, April 2002. % ** % ** This procedure produces: % ** % ** y = chol(A+E), where E is a diagonal matrix with each element as small % ** as possible, and A and E are the same size. E diagonal values are % ** constrained by iteravely updated Gerschgorin bounds. % ** % ** REFERENCES: % ** % ** Jeff Gill and Gary King. 1998. “`Hessian not Invertable.’ Help!” % ** manuscript in progress, Harvard University. % ** % ** Robert B. Schnabel and Elizabeth Eskow. 1990. “A New Modified Cholesky % ** Factorization,” SIAM Journal of Scientific Statistical Computating, % ** 11, 6: 1136-58. % ** % ** % ** % ** Stephane Adjemian (2003): translation from Gauss to Matlab. % */ function AA = generalized_cholesky2(A)

n = size(A,1); L = zeros(n,n); deltaprev = 0; gamm = max(abs(diag(A))); tau = eps^(1/3);

if min(eig(A)) > 0;
tau = -1000000;

end;

norm_A = max(sum(abs(A))’); gamm = max(abs(diag(A))); delta = max([eps*norm_A;eps]); Pprod = eye(n);

if n > 2;
for k = 1,n-2;
if min((diag(A(k+1:n,k+1:n))’ - A(k,k+1:n).^2/A(k,k))’) < tau*gamm ...
& min(eig(A((k+1):n,(k+1):n))) < 0;

[tmp,dmax] = max(diag(A(k:n,k:n))); if A(k+dmax-1,k+dmax-1) > A(k,k);

P = eye(n); Ptemp = P(k,:); P(k,:) = P(k+dmax-1,:); P(k+dmax-1,:) = Ptemp; A = P*A*P; L = P*L*P; Pprod = P*Pprod;

end; g = zeros(n-(k-1),1); for i=k:n;

if i == 1;
sum1 = 0;
else;
sum1 = sum(abs(A(i,k:(i-1)))’);

end;

if i == n;
sum2 = 0;
else;
sum2 = sum(abs(A((i+1):n,i))); end;

g(i-k+1) = A(i,i) - sum1 - sum2;

end; [tmp,gmax] = max(g); if gmax ~= k;

P = eye(n); Ptemp = P(k,:); P(k,:) = P(k+dmax-1,:); P(k+dmax-1,:) = Ptemp; A = P*A*P; L = P*L*P; Pprod = P*Pprod;

end; normj = sum(abs(A(k+1:n,k))); delta = max([0;deltaprev;-A(k,k)+normj;-A(k,k)+tau*gamm]); if delta > 0;

A(k,k) = A(k,k) + delta; deltaprev = delta;

end;

end; A(k,k) = sqrt(A(k,k)); L(k,k) = A(k,k); for i=k+1:n;

if L(k,k) > eps;
A(i,k) = A(i,k)/L(k,k);
end;
L(i,k) = A(i,k);

A(i,k+1:i) = A(i,k+1:i) - L(i,k)*L(k+1:i,k)’; if A(i,i) < 0;

A(i,i) = 0;

end;

end;

end;

end; A(n-1,n) = A(n,n-1); eigvals = eig(A(n-1:n,n-1:n)); dlist = [ 0 ; deltaprev ;...

-min(eigvals)+tau*max((inv(1-tau)*max(eigvals)-min(eigvals))|gamm) ];
if dlist(1) > dlist(2);
delta = dlist(1);
else;
delta = dlist(2);

end; if delta < dlist(3);

delta = dlist(3);

end; if delta > 0;

A(n-1,n-1) = A(n-1,n-1) + delta; A(n,n) = A(n,n) + delta; deltaprev = delta;

end; A(n-1,n-1) = sqrt(A(n-1,n-1)); L(n-1,n-1) = A(n-1,n-1); A(n,n-1) = A(n,n-1)/L(n-1,n-1); L(n,n-1) = A(n,n-1); A(n,n) = sqrt(A(n,n) - L(n,(n-1))^2); L(n,n) = A(n,n); AA = Pprod’*L’*Pprod’;

mmf.math.linalg.cholesky.se99.modchol(A)[source]

Notes

Based on the MATLAB code from the Spatial Econometric Toolkit by James LeSage:

function [l,d]=modchol(A)
% PURPOSE: Modified Cholesky algorithm of Elizabeth Eskow and Robert B. Schnabel
%          Performs a modified cholesky factorization
%          of a SYMMETRIC MATRIX A, of the form P'*A*P + d = L*L'
% -----------------------------------------------------------------------------
% USAGE: [l,d] = modchol(A)
% where: A = symmetric input matrix
%        L = cholesky matrix
%        d = the minimal diagonal increment according to the Gerschgorin Circle Theorem
% ------------------------------------------------------------------------------
% NOTES: Useful for dealing with ill-conditioned numerical hessians and the like
% Schnabel, R. B. and Eskow, E. 1990. "A New Modified Cholesky Factorization."
% SIAM Journal of Scientific Statistical  Computing 11, 1136-58.)
%
% Altman, M., J. Gill and M. P. McDonald.  2003.  Numerical Issues in Statistical
% Computing for the Social Scientist}.  John Wiley \& Sons, has a nice
% discussion of this and R-code for this algorithm at:
% http://www.hmdc.harvard.edu/numerical_issues/
% ------------------------------------------------------------------------------

% Jim LeSage

n=max(size(A));
gamma=max(abs(diag(A)));
psi=max(max(abs(A-diag(diag(A)))));
delta=eps*max(gamma+psi,1);
Bet=sqrt( max([gamma,psi/sqrt(n^2-1),eps]));
for k=1:n
c(k,k)=A(k,k);
end;
[q,dummy]=max(abs(diag(c)));
for j=1:n %compute jth col of L
        l(j,j)=1;
        for s=1:j-1
        l(j,s)=c(j,s)/d(s);
        end
        for i=j+1:n
        lc=0;
                for s=1:j-1
                lc=lc+l(j,s)*c(i,s);
                end;
        c(i,j)=A(i,j)-lc;
        end
        theta(j)=0;
        if (j <=n)
        mc=0;
                for i=j+1:n
                        if abs(c(i,j)) >mc
                        mc= abs(c(i,j)) ;
                        end
                        theta(j)=mc;
                end
        end;
        tt=[abs(c(j,j)),(theta(j)/Bet)^2,delta];
        d(j)=max(tt);
        if (j<n)
                for i=j+1:n
                c(i,i)=c(i,i)-c(i,j)^2/d(j);
                end;
        end;
end
mmf.math.linalg.cholesky.se99.air_modchol(A)[source]

This is based on the following c code from the AIR project:

/* Copyright 2000-2002 Roger P. Woods, M.D. */
/* Modified 7/19/02 */

/*
 * This implements the revised modified Cholesky factorization
 * algorithm described by Schnabel and Eskow.
 *
 * If A is not positive definite, it solves a nearby matrix that is.
 *
 * Schnabel RB, Eskow E, A revised modified Cholesky factorization
 * algorithm,  Siam J Optim., 1999;9(4):1135-1148.
 *
 * Schnabel RB, Eskrow E. A new modified Cholesky factorization. Siam
 * J Sci Stat Comput, 1990;11(6):1136-1158
 *
 * Note that for a sufficiently positive definite matrix, the method is
 * effectively Algorithm 4.2.4 in the 2nd edition of Golub and van Loan's
 * Matrix Computations
 *
 * Returns 0 if matrix was sufficiently positive definite
 * Returns 1 if some other nearby matrix had to be factored
 */

#include "AIR.h"
#include <float.h>

unsigned int AIR_modchol(double **a, const unsigned int n, unsigned int *ipvt, double *g)

{
  double gamma=0.0;
  const double mu=0.1;
  const double tau=pow(DBL_EPSILON,1.0/3.0);
  const double tauhat=tau*tau;

  {
    unsigned int i;

    for(i=0;i<n;i++){

      double temp=fabs(a[i][i]);
      if(temp>gamma) gamma=temp;
    }
  }

{
    unsigned int j;

    /* Phase I, A is potentially positive definite */

    for(j=0;j<n;j++){

      unsigned int imax=j;

      {
        double min=a[j][j];
        double max=min;

        {
          unsigned int i;

          for(i=j+1;i<n;i++){

            double temp=a[i][i];

            if(temp<min) min=temp;
            else if(temp>max){
              max=temp;
              imax=i;
            }
          }
        }
        if(max<tauhat*gamma) break;
        if(min<-mu*max) break;
      }
      /* Pivot on maximum diagonal of remaining submatrix */

      ipvt[j]=imax;

      if(imax!=j){

        {
          double temp=a[j][j];

          a[j][j]=a[imax][imax];
          a[imax][imax]=temp;
        }
        {
          unsigned int i;

          for(i=0;i<j;i++){

            double temp=a[j][i];
            a[j][i]=a[imax][i];
            a[imax][i]=temp;
          }
        }
        {
          unsigned int i;

          for(i=imax+1;i<n;i++){

            double temp=a[i][imax];
            a[i][imax]=a[i][j];
            a[i][j]=temp;
          }
        }
        {
          unsigned int i;

          for(i=j+1;i<imax;i++){

            double temp=a[i][j];
            a[i][j]=a[imax][i];
            a[imax][i]=temp;
          }
        }
      }
      {
        if(j<n-1){

          double min=a[j+1][j+1]-a[j+1][j]*a[j+1][j]/a[j][j];

          {
            unsigned int i;

            for(i=j+2;i<n;i++){

              double temp=a[i][i]-a[i][j]*a[i][j]/a[j][j];
              if(temp<min) min=temp;
            }
          }
          if(min<-mu*gamma) break;
        }

        /* Perform jth iteration of factorization */
        a[j][j]=sqrt(a[j][j]);
        {
          unsigned int i;

          for(i=j+1;i<n;i++){

            a[i][j]/=a[j][j];
            {
              unsigned int k;

              for(k=j+1;k<=i;k++){
                a[i][k]-=a[i][j]*a[k][j];
              }
            }
          }
        }
      }
    }

    if(j==n) return 0;

/* Phase two, a not positive definite */
    if(j==n-1){

      double delta=tau*(-a[j][j])/(1-tau);
      double temp=tauhat*gamma;

      ipvt[j]=j;

      if(temp>delta) delta=temp;

      a[j][j]=sqrt(delta);
      return 1;
} else{
      unsigned int k=j;
      double deltaprev=0.0;

      /* Calculate the lower Gerschgorin Bounds of a[k]*/
      {
        unsigned int i;

        for(i=k;i<n;i++){

          g[i]=a[i][i];

          {
            unsigned int j1;

            for(j1=k;j1<i;j1++){

              g[i]-=fabs(a[i][j1]);
            }
          }
          {
            unsigned int j1;

            for(j1=i+1;j1<n;j1++){

              g[i]-=fabs(a[j1][i]);
            }
          }
        }
      }
      {
        /* Modified Cholesky decomposition */
        unsigned int j1;

        for(j1=k;j1+2<n;j1++){

          unsigned int imax=j1;
          double max=g[j1];

          /* Pivot on maximum lower Gerschgorin bound estimate */
          {
            unsigned int i;

            for(i=j1+1;i<n;i++){

              if(g[i]>max){
                max=g[i];
                imax=i;
              }
            }
          }
          ipvt[j1]=imax;
          if(imax!=j1){

            {
              double temp=a[j1][j1];

              a[j1][j1]=a[imax][imax];
              a[imax][imax]=temp;
            }
            {
              unsigned int i;

              for(i=0;i<j1;i++){

                double temp=a[j1][i];
                a[j1][i]=a[imax][i];
                a[imax][i]=temp;
              }
            }
            {
              unsigned int i;

              for(i=imax+1;i<n;i++){

                double temp=a[i][imax];
                a[i][imax]=a[i][j1];
                a[i][j1]=temp;
              }
            }
            {
              unsigned int i;

              for(i=j1+1;i<imax;i++){

                double temp=a[i][j1];
                a[i][j1]=a[imax][i];
                a[imax][i]=temp;
              }
            }
          }
          /* Calculate E[j1][j1] and add to diagonal */
          {
            double normj=0.0;
            double delta;

            {
              unsigned int i;

              for(i=j1+1;i<n;i++){

                normj+=fabs(a[i][j1]);
              }
            }
            delta=normj;
            if(tauhat*gamma>delta){
              delta=tauhat*gamma;
            }
            delta-=a[j1][j1];
            if(delta<0.0) delta=0.0;
            if(delta<deltaprev) delta=deltaprev;

            if(delta>0.0){
              a[j1][j1]+=delta;
              deltaprev=delta;
            }

            /* Update Gerschgorin bound estimates */
            if(a[j1][j1]!=normj){

              double temp=1-normj/a[j1][j1];

              {
                unsigned int i;

                for(i=j1+1;i<n;i++){

                  g[i]+=fabs(a[i][j1])*temp;
                }
              }
            }
          }
          /* Perform j1th iteration of factorization */
          a[j1][j1]=sqrt(a[j1][j1]);
          {
            unsigned int i;

            for(i=j1+1;i<n;i++){

              a[i][j1]/=a[j1][j1];
              {
                unsigned int k1;

                for(k1=j1+1;k1<=i;k1++){

                  a[i][k1]-=a[i][j1]*a[k1][j1];
                }
              }
            }
          }
        }
      }
      /* Final 2x2 submatrix */
      {
        double lambdahi=a[n-2][n-2]-a[n-1][n-1];
        double lambdalo;

        ipvt[n-2]=n-2;
        ipvt[n-1]=n-1;

        lambdahi=lambdahi*lambdahi;
        lambdahi+=4.0*a[n-1][n-2]*a[n-1][n-2];
        lambdahi=sqrt(lambdahi);
        lambdalo=-lambdahi;
        lambdahi+=(a[n-2][n-2]+a[n-1][n-1]);
        lambdalo+=(a[n-2][n-2]+a[n-1][n-1]);
        lambdahi/=2.0;
        lambdalo/=2.0;
        {
          double delta=tau*(lambdahi-lambdalo)/(1-tau);

          if(tauhat*gamma>delta) delta=tauhat*gamma;
          delta-=lambdalo;
          if(delta<0.0) delta=0.0;
          if(delta<deltaprev) delta=deltaprev;
          if(delta>0.0){
            a[n-2][n-2]+=delta;
            a[n-1][n-1]+=delta;
            deltaprev=delta;
          }
          a[n-2][n-2]=sqrt(a[n-2][n-2]);
          a[n-1][n-2]/=a[n-2][n-2];
          a[n-1][n-1]=sqrt(a[n-1][n-1]-a[n-1][n-2]*a[n-1][n-2]);
        }
      }
      return 1;
    }
  }
}

Navigation

© Copyright 2010, Michael McNeil Forbes. Last updated on 17 September 2012. Created using Sphinx 1.1.3.