mmf.math.linalg.cholesky.cholesky_¶
| se99(A) | Return (L, e): the Schnabel-Eskow generalized Cholesky |
Modified Cholesky.
This module provides different methods for computing the Modified
Cholesky Factorization of a symmetric matrix 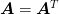 :
:
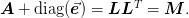
These algorithms attempt to satisfy the following goals:
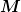 is safely symmetric positive definite (SPD) and well
conditioned.
is safely symmetric positive definite (SPD) and well
conditioned.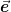 is as small as possible, meaning that it is zero if
is as small as possible, meaning that it is zero if 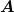 is
already SPD and not much larger than the most negative eigenvalue
is
already SPD and not much larger than the most negative eigenvalue
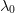 of
of 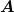 . The figure of merit in this sense is
usually
. The figure of merit in this sense is
usually 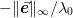 .
.- Efficient computational efficiency.
The original algorithms
| [GM74] | Philip E. Gill and Walter Murray, “Newton-type methods for unconstrained and linearly constrained optimization”, Mathematical Programming 7(1), 311 – 350 (1974). |
| [GMW81] | P. E. Gill, W. Murray, and M. H. Wright, “Practical Optimization”, Academic Press, London, (1981). |
| [SE90] | Robert B. Schnabel and Elizabeth Eskow, “A New Modified Cholesky Factorization”, SIAM Journal on Scientific and Statistical Computing 11(6), 1136-1158 (1990). |
| [SE99] | Robert B. Schnabel and Elizabeth Eskow, `”A Revised Modified Cholesky Factorization Algorithm” <>`_, SIAM Journal on Optimization 9(4), 1135 – 1148 (1999). |
Codes¶
GMW81:
proc gmchol(A);
/* calculates the Gill-Murray generalized choleski decomposition */
/* input matrix A must be non-singular and symmetric */
/* Author: Jeff Gill. Part of the Hessian Project. */
local i,j,k,n,sum,R,theta_j,norm_A,phi_j,delta,xi_j,gamm,E,beta_j;
n = rows(A);
R = eye(n);
E = zeros(n,n);
norm_A = maxc(sumc(abs(A)));
gamm = maxc(abs(diag(A)));
delta = maxc(maxc(__macheps*norm_A~__macheps));
for j (1, n, 1);
theta_j = 0;
for i (1, n, 1);
sum = 0;
for k (1, (i-1), 1);
sum = sum + R[k,i]*R[k,j];
endfor;
R[i,j] = (A[i,j] - sum)/R[i,i];
if (A[i,j] -sum) > theta_j;
theta_j = A[i,j] - sum;
endif;
if i > j;
R[i,j] = 0;
endif;
endfor;
sum = 0;
for k (1, (j-1), 1);
sum = sum + R[k,j]^2;
endfor;
phi_j = A[j,j] - sum;
if (j+1) <= n;
xi_j = maxc(abs(A[(j+1):n,j]));
else;
xi_j = maxc(abs(A[n,j]));
endif;
beta_j = sqrt(maxc(maxc(gamm~(xi_j/n)~__macheps)));
if delta >= maxc(abs(phi_j)~((theta_j^2)/(beta_j^2)));
E[j,j] = delta - phi_j;
elseif abs(phi_j) >= maxc(((delta^2)/(beta_j^2))~delta);
E[j,j] = abs(phi_j) - phi_j;
elseif ((theta_j^2)/(beta_j^2)) >= maxc(delta~abs(phi_j));
E[j,j] = ((theta_j^2)/(beta_j^2)) - phi_j;
endif;
R[j,j] = sqrt(A[j,j] - sum + E[j,j]);
endfor;
retp(R'R);
endp;
- mmf.math.linalg.cholesky.cholesky_.se99(A)[source]¶
Return (L, e): the Schnabel-Eskow generalized Cholesky decomposition of M = A + diag(e) = dot(L, L.T) where
- M is safely symmetric positive definite (SPD) and well conditioned.
- e is small (zero if A is already SPD and not much larger than the most negative eigenvalue of A)
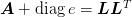
Parameters : A : array
Must be a non-singular and symmetric matrix
test : bool
If True, use the directly translated iterative code for testing.
Returns : L : 2d array
Lower triangular Cholesky factor.
e : 1d array
Diagonals of correction matrix E.
Examples
>>> np.random.seed(3) >>> A = np.random.rand(100,100)*2 - 1 >>> A = A + A.T >>> L, e = sechol(A) >>> np.allclose(np.dot(L,L.T), (A + np.diag(e))) True >>> np.linalg.eigvalsh(A).min() ()
>>> A2 = np.array([[-0.451, -0.041, 0.124], ... [-0.041, -0.265, 0.061], ... [ 0.124, 0.061, -0.517]]) >>> L, e = sechol(A2, test=True) >>> e.max()/np.linalg.eigvalsh(A).min()
This is based on the code in