Back to Theory Basic Concepts Harmonic Loading Impedance Ratio Transfer Function Numerical Solution Fourier Analysis	Dr. Layer 1.0 An Introduction to the Theory of Wave Propagation in Layer Media Material Boundary in an Elastic Half-space
	Introduction
	Impedance Ratio Coefficients    Consider a harmonic stress wave traveling along an elastic half-space in the +z direction and approaching an interface between two different materials, as shown in Figure 1. Since the wave is traveling towards the interface, it will be referred as incident wave. Since it is traveling in material 1, its wave-length will be l1=2p/k1, and it can therefore be described by Figure 1. One Dimensional Wave Propagation at Material Interface (1) 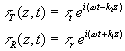When the incident wave reaches the interface, part of the energy will be transmitted through the interface to continue traveling in the positive z-direction through material 2. This transmitted wave will have a wavelength l2=2p/k2. The remainder will be reflected at the interface and will travel back through material 1 in the negative z-direction as a reflected wave. The transmitted and reflected waves can be described by  (2a) (2b) Assuming that the displacements associated with each of these waves are of the same harmonic form as the stresses that cause them; that is 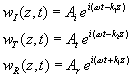(3a) (3b) (3c) 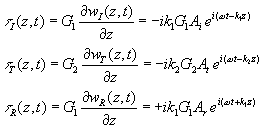Stress-strain and strain-displacement relationships can be used to relate the stress amplitudes to the displacement amplitudes: (4a) (4b) (4c) 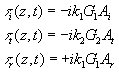From these, the stress amplitudes are related to the displacement amplitudes by (5a) (5b) (5c) At the interface, both compatibility of displacements and continuity of stresses must be satisfied. The former requires that (6) and the latter that (7) Substituting equations (3) and (4) into equations (6) and (7), respectively, indicates that (8a) (8b) at the interface. Substituting equations (5) into equation (8b) and using the relationship kG = wrvs, gives (9) Equation (9) can be rearranged to relate the displacement amplitude of the reflected wave to that of the incident wave: (10) and knowing Ai and Ar, equation (8a) can be used to determine At as (11) Remember that the product of the density and the wave propagation velocity is the specific impedance of the material. Equations (10) and (11) indicate that the partitioning of the energy at the interface depends only on the ratio of the specific impedances of the materials on either side of the interface. Defining the impedance ratio as az=r2vs2/r1vs1, the displacement amplitudes of the reflected and transmitted waves are (12) (13)  After evaluating the effect of the interface on the displacement amplitudes of the reflected and transmitted waves, its effect on stress amplitudes can be investigated. From equations (5) (14a) (14b) (14c) Substituting equations (14) into equations (12) and (13) and rearranging gives (15) (16)   Interesting Impedance Ratio Phenomena The importance of the impedance ratio in determining the nature of the reflection and transmission at interfaces can clearly be seen. Equations (12), (13), (15), and (16) indicate that fundamentally different types of behavior occur when the impedance ratio is less than or greater than 1. When the impedance ratio is less than 1, an incident wave can thought of as approaching a “softer” material. For this case, the reflected wave will have a smaller stress amplitude than the incident wave and its sign will be reversed. If the impedance ratio is greater than 1, the incident wave is approaching a “stiffer” material in which the stress amplitude of the transmitted wave will be greater than that of the incident wave and the stress amplitude of the reflected wave will be less than, but of the same sign, as that of the incident wave. The displacements amplitudes are also affected by the impedance ratio. The relative stress and displacement amplitudes of reflected and transmitted waves at boundaries with several different impedance ratios are illustrated in Table 1. Table 1 Influence of Impedance Ratio on Displacement and Stress Amplitudes of Reflected and Transmitted Waves Impedance Ratio Displacement Amplitudes Stress Amplitudes az Incident Reflected Transmitted Incident Reflected Transmitted 0 Ai Ai 2Ai si -si 0 1/4 Ai 3Ai/5 8Ai/5 si -3si/5 2si/5 1/2 Ai Ai/3 4Ai/3 si -si/3 2si/3 1 Ai 0 Ai si 0 si 2 Ai -Ai/3 2Ai/3 si si/3 4si/3 4 Ai -3Ai/5 2Ai/5 si 3si/5 8si/5 ¥ Ai -Ai 0 si si 2si The cases of az=0 and az=¥ are of particular interest. An impedance ratio of zero implies that the incident wave is approaching a “free end” across which no stress can be transmitted (tt=0). To satisfy this zero stress boundary condition, the displacement of the boundary (the transmitted displacement) must be twice the displacement amplitude of the incident wave (At=2Ai). The reflected wave has the same amplitude as the incident wave but is of the opposite polarity (tr=-ti). In other words, a free end will reflect a compression wave as a tension wave of identical amplitude and shape and a tension wave as an identical compression wave. An infinite impedance ratio implies that the incident wave is approaching a “fixed end” at which no displacement can occur (wt=0). In that case the stress at the boundary is twice that of the incident wave (tt=2ti) and the reflected wave has the same amplitude and polarity as the incident wave (Ar=-Ai). The case of az=1, in which the impedances on each side of the boundary are equal, is also of interest. Equations (12), (13), (15), and (16) indicate that no reflected wave is produced and that the transmitted wave has, as expected, the same amplitude and polarity as the incident wave. In other words, all of the elastic energy of the wave crosses the boundary unchanged and travels away, never to return. Another way of looking at a boundary with an impedance ratio of unity is as a boundary between two identical semi-infinite media. 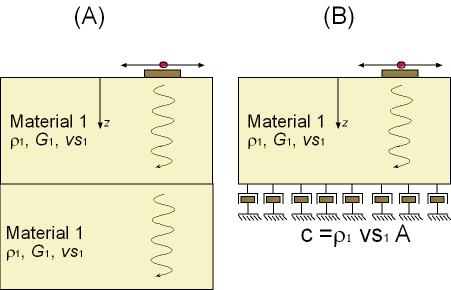A harmonic wave traveling in the positive z-direction (Figure 2-A) would impose an axial force  [(see equation()] on the boundary Figure 2. (A)Harmonic shear wave traveling along two connected soil layers; (B) Soil layer connected to a dashpot (19) This force is identical to that which would exist if the semi-infinite medium on the right side of the boundary were replaced by a dashpot (Figure 2-B) of coefficient c=rvsA. In other words, the dashpot would absorb all the elastic energy of the incident wave, so the response of the medium on the top would be identical for both cases illustrated in Figure 2-B. This result has important implications for ground response and soil-structure interaction analyses, where the replacement of a semi-infinite domain by discrete elements such as dashpots can provide tremendous computational efficiencies. References Kramer, S. L. (1996), "Geotechnical Enarthquake Engineering", Prentice Hall.
BACK TO TOP  Last Updated: 11/21/00	Contact us at: parduino@u.washington.edu