Dr. Layer
1.0
An
Introduction to the Theory of Wave Propagation in Layer Media
Harmonic Loading
Traveling Waves
Let us consider an expression for the longitudinal displacement of the form
 |
(1)
|
where the amplitude A is independent of x and t. Equation (1) is of the general form f(x-ct) and thus clearly represents a traveling wave. The argument k(x-ct) is called the phase of the wave; points of constant phase are propagated with the phase velocity c. At any instant t, u(x,t) is a periodic function of x with wavelength l, where l=2p/k. The quantity k=2p/l, which counts the number of wavelengths over 2p, is termed the wavenumber. At any position the displacement u(x,t) is time-harmonic with time period T, where T=2p/w. The circular frequency w follows from ( ) as
 |
(2)
|
It follows that an alternative representation of u(x,t) is
 |
(3)
|
Equations ( ) and ( ) are called traveling harmonic waves. The expressions represent trains of sinusoidal waves, which disturb at any instant of time the complete (unbounded) extend of the medium. Harmonic waves are steady-state waves, as opposed to the transient waves (pulses) which were introduced in the previous theoretical handout.
By substituting ( ) into the wave equation ( ) we obtain
 |
(4)
|
Equations ( ) show that the phase velocities of traveling harmonic waves in one-dimensional longitudinal strain are independent of the wavelength l.This implies that very short waves propagate with the same phase velocity as long waves. If the phase velocity does not depend on the wavelength we say that the system is nondispersive. If the material is notpurely elastic but displays dissipative behavior, it is found that the phase velocity of harmonic waves depend on the wavelength, and the system is said to be dispersive. Dispersion is an important phenomenon because it governs the change in shape of a pulse as it propagates through a dispersive medium
The phase velocity c should be clearly
distinguished from the particle velocity 
, which
is obtained as
 |
(5)
|
For one-dimensional longitudinal or shear strain the maximum value of the ratioof the particle velocity and the phase velocity is thus obtained as
 |
(6)
|
Within the range of validity of the linear theory the ratio A/k should be much less than unity.
Complex Notation
For mathematical convenience we generally use, instead of ( ), the expression
 |
(7)
|
where 
. Withoutn
stating it explicitly, henceforth it is understood that the real or imaginary
part of ( ) is to be taken for the physical interpretation of the solution.
For the case of one-dimensional shear strains the corresponding shear
stress is then represented by
 |
(8)
|
and the particle velocity is written as
 |
(9)
|
Standing Waves
Let us consider two displacement waves of the same frequency and wavelength, but traveling in opposite directions. Since the wave equation is linear the resultant displacement is
 |
(10)
|
where A+ and A- are real-valued amplitudes, and g+ and g- are phase angles. If the amplitudes of the two simple harmonic waves are equal, A+ = A- = A, we can write
 |
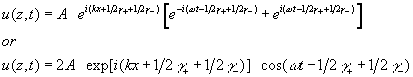(11)
|
The real part of this expression is
 |
(12)
|
Equation ( ) represent a standing wave, since the shape of the wave does not travel. At points where cos( kx + 1/2 g+ + 1/2 g- ) = 0, the two traveling waves always cancel each other and the medium is at rest. These points are called nodal points. Halfway between each pair of nodal points are the antinodes, where the motion has the largest amplitude.
Modes of Vibration
Standing waves form certain modes of free vibration of an elastic body. As an example we consider the vibrations of a rod. If we consider a semi-infinite rod and if we require that the displacement vanishes at x = 0, the possible harmonic motions are subject to restrictions. Equation (1) can now not be used and we have to employ the standing wave form ( ) with the angles g+ and g- chosen so that a nodal point coincides with the boundary x = 0, i.e.,
 |
(13)
|
 |
(14)
|
When, as a second boundary condition we add u=0 at x=l, the harmonic motion is still further limited, for now of all the harmonic motions represented by ( ) only those which have a nodal point at x=l can be used. Thus we require
 |
(15)
|
which implies
 |
(16)
|
The distance between nodal points is half the wavelength, and thus this distance must be l, l/2, l/3, etc. The corresponding circular frequencies are
 |
(17)
|
The circular frequency of the lowest or fundamental mode, which is called the fundamental frequency, is w0 = p ns/l radians per second; in cycles per second the fundamental frequency is f0 = ns/2l. The frequencies of the higher modes are in cycles per second, f2 = 2ns/2l, f3 = 3ns/2l, etc. The higher frequencies are called overtones. For the example of the rod with rigidly supported ends the overtones are integral multiples of the fundamental frequency. Overtones with this simple relation to the fundamental are called harmonics. Only for the simplest vibrating systems governed by the wave equation are the modes of vibration as simple as discussed in this section.
Last
Updated:
11/21/00
Contact us at: parduino@u.washington.edu