|
|
Inversion-based Feedforward
|
Inversion of System dynamics can be used to find feedforward
inputs that achieve high-precision positioning
--- see
conceptual description of the inversion-based
feedforward for precision control.
Our research developed procedures to find bounded inverses for non-minimum
phase systems (such inverses tended to be unbounded using standard methods);
quantified the circumstances under which inverses can improve performance even in the
presence of plant uncertainty; and developed an optimal-inversion method that
can be applied to non-square systems. Some of the key developments are summarized below.
|
Issue 1: Inversion of Nonlinear Non-minimum Phase Systems
Background: Research in the 1960s and 1970s showed
that a system's dynamics can be inverted to find inputs that
exactly track a desired output trajectory. For example, system
inversion can be used to find control inputs that enable an aircraft
to track a desired maneuver. These standard inversion methods led,
however, to unbounded inputs for nonminimum phase systems -- such systems
can be characterized as having "unstable" inverse systems.
Thus, the standard inversion method with unbounded inputs could
not be applied to practical nonminimum phase systems such as
flexible structures with non-collocated sensors and actuators.
In the past, other researchers sought to alleviate this
inability to invert nonminimum phase systems by relaxing the
problem, e.g., (a) inverting a modified system that is not
nonminimum phase, i.e., minimum phase, (b) changing the
desired output trajectory, i.e., tracking a different output
to enable inversion or (c) tracking the output asymptotically
if it belongs to a special class of exogenous signals.
Our early research (Ref 1)
provided a breakthrough by directly solving the inversion
problem for nonlinear nonminimum phase systems.
It developed and proved the convergence of a
Picard-like iteration to obtain bounded inverses for
nonlinear nonminimum phase systems. The use of stable
(but possibly non-causal) output-to-input maps enabled us to
find bounded solutions to "unstable" inverse systems.
(MATLAB Code used in Ref 1
can be downloaded here.)
|
Issue 2: Inversion under Plant Uncertainty
Background: In general, any inversion-based approach,
e.g., the approach in
Ref 1,
to precision tracking
is a model-based approach; hence, its performance depends
on the accuracy of the model. For example, model-based inversion can
be used to achieve high-precision, output tracking
if the models are relatively accurate. Anecdotal
experimental evidence showed, however, that large errors
in computing the inverse input (due to errors in the models)
can adversely affect the output-tracking performance.
These observations led to the basic question
"Should model-based inversion be used for precision output-tracking
in the presence of modeling uncertainties?"
The above fundamental question was answered by our research
(Ref 2),
which found bounds on size of model uncertainties
so that the inversion-based input together with a feedback
input beats the output-tracking performance of the feedback alone.
Moreover the research developed algorithms to find inverses when the
modeling uncertainty varies with frequency. This development is
important in practical applications because modeling uncertainty
typically tends to grow and become large at high frequencies.
|
Issue 3: Managing Non-causality of the Inverse
Background: An important challenge in
implementing the inversion approach
(Ref 1)
is that the inputs are non-causal for nonminimum phase systems;
hence the input needs be changed before the output is modified.
While it is intuitive that preview information of the desired output
can be used to find the current value of the inverse input,
the challenge is to address the question, "how much of the future
output trajectory information is needed to achieve a desired
precision in output tracking?"
This question was addressed by our research group
(see Ref 3);
we quantified the amount of preview information needed to achieve
a desired precision in output tracking and developed an algorithm
for online implementation of the non-causal inverse input.
In
Ref 4,
we also experimentally verified the preview-based method
and achieved sub-nano-scale positioning in a Scanning Tunneling Microscope
when imaging carbon atoms in graphite.
The theory was extended to nonlinear systems
in Ref 5.
|
Issue 4: Inversion for Non-Square Systems and To Handle Actuator Limits
Background: Standard inversion methods are applicable to square
systems with the same number of outputs as inputs. A challenge is
to extend the approach to nonsquare systems, say, with actuator
redundancy. Similarly, in some situations, a systematic approach is needed
to trade off the tracking requirement to manage system limitations such as
actuator bandwidth restrictions.
Our research developed optimal inversion methods
to account for actuator saturation and
bandwidth limitations (e.g., Ref 6). While the formulation of the problem
is similar
to standard optimal control theory, the optimal inverse
has an explicit solution. The same optimal inversion method
was extended to develop
inverses for non-square systems, e.g., to handle actuator
redundancy,
Ref 7.
|
Issue 5: Output Transition Versus State Transition
Background:
The minimum-time, state transition problem
with bounds on the input magnitude is a classical problem
that leads to a bang-bang-type input for the fastest state transition.
However, the transition time can be reduced further
if only the system output needs to be transitioned
from one value to another (in time interval [0,T])
rather than the entire system state.
The time-optimal output transition problem is to change the system output
from an initial value y1 (for all time t before t=0) to a final value y2
(for all time t after t=T).
The main contribution of our work is to solve the optimal output
transition problem (e.g.,
Ref 8
and Ref 9). It uses inversion-based
feedforward to maintain the output (using pre- and post-actuation)
at the desired values, y1 and y2 respectively, outside of the
output-transition interval [0, T]. The original approach minimized time and
energy for optimizing the transition. The minimum-time transition problem
was solved with extension to
nonlinear systems in Ref 10 and dual-stage systems in Ref 11.
Our theoretical developments
on inversion-based output transitions were applied to
Disk Drive servo systems in Ref 12 – this work was partially funded by
INSIC,
which is a consortium of Disk Drive companies.
A description of the feedforward control to
nano-positioning for high-density storage systems
can be found in this
presentation.
|
Application to Nanopositioning
A review of feedforward control and its application to
nanopositioning can be found in
Ref 13.
This article reviews inversion-based feedforward approaches used for high-speed
nanopositioning such as optimal inversion that accounts for model
uncertainty and inversion-based iterative control for repetitive
applications.
The article establishes connections to other
existing methods such as zero-phase-error-tracking
feedforward and robust feedforward.
Nanopositioning is also reviewed in the following presentation
slides.
|
|
|
Contact Santosh Devasia:
devasia@u.washington.edu
|
|
|
|
Related Presentations
|
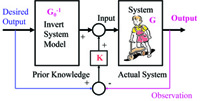
Inversion-based Feedforward Theory (Conceptual Slides)
|



Application of Feedforward to Nanopositioning
|

Application of Feedforward to Disk Drives:
Presentation to the Information Storage Industry Consortium
(INSIC)
|
References
Ref 1:
S. Devasia, D. Chen and B. Paden
"Nonlinear Inversion-Based
Output Tracking,"
IEEE Transactions on Automatic Control, Vol. 41 (7),
pp. 930-942, July 1996.
Ref 2:
S. Devasia
"Should Model-based Inverse Inputs be
used as Feedforward under Plant Uncertainty?"
IEEE Trans. on
Automatic Control, Vol. 47(11), pp. 1865-1871, Nov 2002.
Ref 3:
Q. Zou and S. Devasia
"Preview-based Stable-Inversion for Output Tracking,"
ASME J. of Dynamic Systems, Measurement and Control, Vol.
121 (4), pp. 625-630, December 1999.
Ref 4:
Q. Zou and S. Devasia
"Preview-based Optimal
Inversion for Output Tracking: Application to Scanning
Tunneling Microscopy,"
IEEE Transactions on Control Systems
Technology, Vol. 12(3), pp. 375-386, May 2004.
Ref 5: Q. Zou and S. Devasia "Precision Preview-based
Stable-Inversion for Nonlinear Nonminimum-Phase Systems:
The VTOL Example," Automatica, Vol. 43 (1), pp. 117-127, January, 2007.
Ref 6: J.S. Dewey, K. K. Leang and S. Devasia
"Experimental and Theoretical Results in Output-Trajectory
Redesign for Flexible Structures," ASME Journal of
Dynamic Systems, Measurement, and Control, Vol. 120 (4),
pp. 456-461, December 1998.
Ref 7:
R. Brinkerhoff and S. Devasia
"Output Tracking for Actuator Deficient/Redundant
Systems: Multiple Piezoactuator Example,"
AIAA J. of Guidance, Control, and Dynamics, Vol. 23
(2), pp. 370-373, March-April 2000.
Ref 8:
H. Perez and S. Devasia
"Optimal Output Transitions for Linear Systems,"
Automatica, Vol. 39(2), pp. 181-192, February 2003.
Ref 9: D. Iamratanakul, H. Perez and S. Devasia
"Minimum-Energy Output-Transitions for Linear Discrete-Time Systems:
Flexible Structure Applications," AIAA Journal of Guidance,
Control, and Dynamics, Vol. 27(4), pp. 572-585, July-August 2004.
Ref 10: S. Devasia "Nonlinear Minimum-Time Control With Pre-
and Post-Actuation." Automatica, Vol. 47 (7), pp. 1379-1387, July 2011.
Ref 11: S. Devasia "Time-Optimal Control with Pre/Post Actuation
for Dual-Stage Systems," IEEE Transactions on Control Systems Technology,
Vol. 20 (2), pp. 323-334, March 2012.
Ref 12: D. Iamratanakul and S. Devasia "Minimum-Time/Energy,
Output Transitions for Dual-Stage Systems," ASME J. of
Dynamic Systems, Measurement and Control, Vol. 131 (2), pp. 1-8, March, 2009
Ref 13:
G. M. Clayton, S. Tien, K. K. Leang, Q. Zou and S. Devasia
"A Review of Feedforward Control Approaches in Nanopositioning for
High Speed SPM,"
ASME Journal of Dynamic Systems, Measurement and
Control, Special Issue on Dynamic Modeling, Control and Manipulation
at the Nanoscale, Vol. 131 (6), Article number 061001, pp. 1-19, Nov. 2009
|
|







