Example 12.1 Time variation of the cell count after a single fraction exposure for different choices of the cell kinetic parameters: Cell birth rate (TCC) and the potential doubling time (TPOT) and constant growth fraction (GF) (rmrsim3.inp -> rmrsim3.out rmrsim4.inp -> rmrsim4.out ). 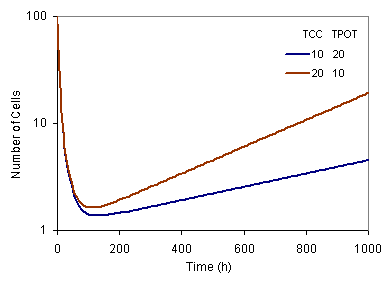 Cell count after single fraction dose exposure for different combinations of the Cell birth rate (TCC) and the potential doubling time (TPOT) Comments: Cell count after single fraction dose exposure for different combinations of the Cell birth rate (TCC) and the potential doubling time (TPOT) Comments:- Increasing the cell birth rate (TCC) and decreasing the potential doubling time (TPOT) increases the cell count as time increases.
- The initial cell count is 100 and a single fraction dose of 2 Gy at 10 Gy/h is assumed.
- GF, the growth factor is held constant at 1.0, i.e., the entire cell population is dividing.
Example 12.2 Time variation of the cell count after a single fraction exposure for different choices of the cell kinetic parameter: Growth fraction (GF) for constant Cell birth rate (TCC) and potential doubling time (TPOT) (rmrsim4.inp -> rmrsim4.out , rmrsim5.inp -> rmrsim5.out). 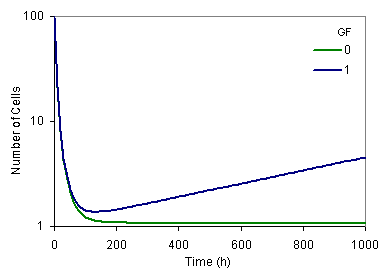 Cell count after single fraction dose exposure for different Growth Fractions (GF) while TCC and TPOT are held constant. Comments: Cell count after single fraction dose exposure for different Growth Fractions (GF) while TCC and TPOT are held constant. Comments:- Parameters TCC and TPOT are held at 10 and 20 hours respectively in order to observe the effect of the Growth Factor GF.
- Choosing the growth fraction to be equal to zero assumes the entire cell population to be non-dividing.
Suggested Problems - Approximately calculate the overall population doubling time for the input description used in Example 12.1.
- Predict the effect of the repair half time on the case of GF=0 in Example 12.2 without doing any calculations. Test the accuracy of your prediction using the input file given in Example 12.2 (choose the one with the GF=0.0).
- Modify one of the input file given in example 12.1 to include a split dose exposure scenario. Choose your input parameters such that variation of the number of cells during the irradiation times, including the split time is detailed. Plot the Number of cells Vs. time and justify the results.
- Examine the effects of repair half time and the growth factor (GF), one at a time, on the calculation you performed under problem 3. Make appropriate plots and justify the variations you observe.
Tip: Experiment by changing the various model parameters and physically interpreting your results.
|


 Cell count after single fraction dose exposure for different combinations of the Cell birth rate (TCC) and the potential doubling time (TPOT) Comments:
Cell count after single fraction dose exposure for different combinations of the Cell birth rate (TCC) and the potential doubling time (TPOT) Comments: Cell count after single fraction dose exposure for different Growth Fractions (GF) while TCC and TPOT are held constant. Comments:
Cell count after single fraction dose exposure for different Growth Fractions (GF) while TCC and TPOT are held constant. Comments: