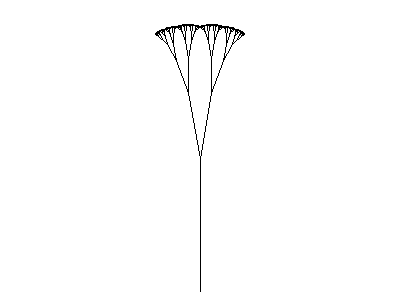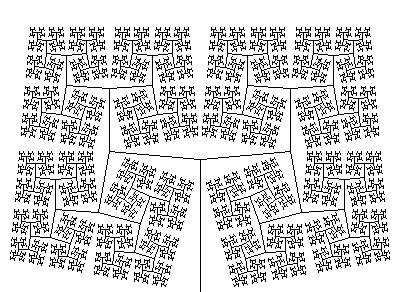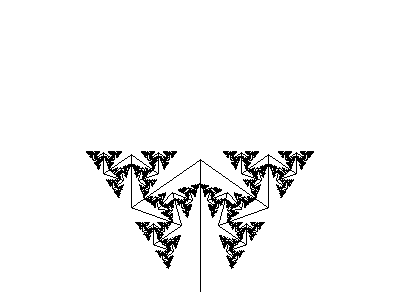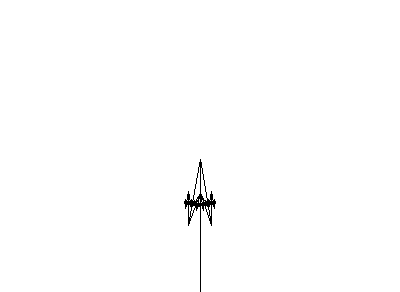
A fractal's appearance may change
with each iteration. This geometric
fractal demonstrates behavior that
is quite different from those in the
Mandelbrot and Julia sets.
| Fractals - Examples and Simulations |
 A fractal's appearance may change with each iteration. This geometric fractal demonstrates behavior that is quite different from those in the Mandelbrot and Julia sets. |
| Serious eye
candy Some
exceptional fractal still images can be found here
and here.
This site features state-of-the-art examples of fractal animation. The animation movie Universe #3X is the "deepest" fractal animation to date. Types of Fractals L-System Fractals
This
applet shows a very wide variety of L-system fractals.
Varying
the controls built into the applet can radically change what type of
image is generated.
IFS FractalsThere are more L-System fractals available at this site, which has a nice catalog of some of the well known fractals in this class. The
Sierpinski triangle (or gasket)
and the fern are examples of IFS (iterated function system)
fractal. Several examples, both deterministic and random, are
available: [ 1
| 2
| 3
| 4 | 5 | 6
].
Another site has some non-interactive samples of IFS fractals. However, it also explains what an IFS fractal is and gives the mathematical formula for it. In addition, it also has complex number fractals--which include the Mandelbrot and Julia Sets--and orbit fractals as well. Pascal's Triangle There
are so many things that can be with Pascal's triangle that looking at
only the fractal aspect of it seems .... well, limited. So
here's
a web page that should properly be titled "More than you ever wanted to
know about Pascal's triangle." After that, look at
these pages [ 1
| 2
].
Mandlebrot and Julia SetsExplore the
Mandelbrot
set: Zoom in on any part of this image to see the
recursive nature of this set.
More Mandelbrot applets with different capabilities are useful for exploring different aspects of the set [ 1 | 2 | 3 | 4 ]. Then try out the Julia and Mandelbrot Set explorer. Click on a point in the Mandelbrot set fractal to see the corresponding Julia set. Collections
Applications
|
| Home
|
Overview
|
History
|
Tutorials
|
Multimedia
and
Lectures Examples and Simulations | Advanced Topics |