PKDGRAV Performance
MPICH and LAM Performance on Astrolab
In this section, we summarize results from our performance experiments on the Astrolab cluster. First we began with a version of PKDGRAV compiled using the standard gcc compiler and MPICH libraries. As we suspected, the performance was quite unpredictable. The problem being that the gcc compiler has a stack alignment problem which causes a reduction in efficiency on a processor of a factor of two and on parallel jobs performs very unpredictably (Fig 1). As you can see the performance actually gets worse in the beginning with the number of processors and in the end performs much worse than the rest. In figure 1 we have plotted the "scaled performance" (flops per clock tick) of PKDGRAV. The megaflop rate per time step is computed by PKDGRAV and is an accurate measurement for comparing the performance as long as the comparison is done between processors of the same family, such as here. We have taken the factory quoted clock speed as fact. This is within reasonable allowances.
In the rest of the tests we used the Portland Group C compiler (pgcc); it does not suffer
from stack misalignment as does gcc. Comparing the MPICH and LAM
versions of PKDGRAV using pgcc, we found that the LAM version
performed much better than the MPICH version on 8, 12, and 16
processors as can be seen in figure 1 and in figure 2. Figure 2 is plot of the raw
performance. As one can see the Roadrunner cluster performance is on
a different scale than the Astrolab cluster. This is due to the
difference in processor speed: Astrolab contains 300Mhz processors and
Roadrunner contains 450Mhz processors. We will discuss more about the
Roadrunner cluster in the next section. Also, note that the first
point is not two processors not one. We would have liked to see the
scaling from one to two processors, but the memory required to run the
test on one processor without disk swapping exceeded the available 256
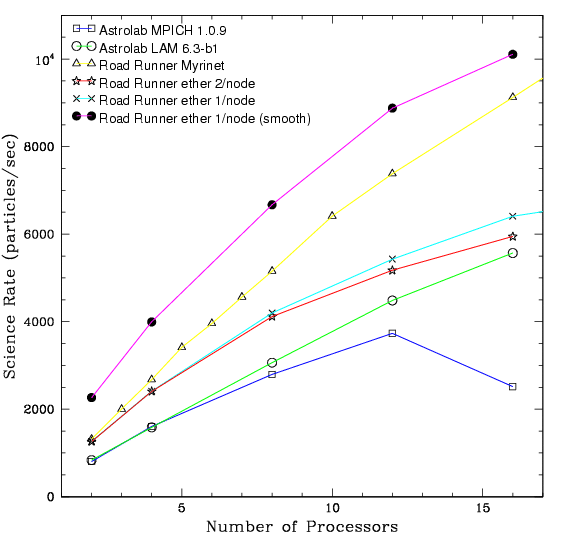
MB on an Astrolab node. As another comparison of performance, in figure 3 we have plotted the "scientific
rate." The scientific rate is defined as the total number of
particles divided by the time taken to advance one time step: this
excludes the domain decomposition and tree building.
LAM's performance peaks at roughly 1.25 Gflops/sec, which is better
than the best recorded rate for such a simulation on the Astrolab
cluster. This comes in just below the Roadrunner performance using only
ethernet. The previous best rate was just 1 Gflop using the MPICH
implementation. The performance difference lies in the construction
of MPICH vs LAM. MPICH is coded in a layered scheme10. Each layer
depends solely on the layer below it and each layer starting from the
lowest level can be taken out and replaced by a more machine specific
layer. This allows users to develop fast message passing systems,
that take full advantage of the local architecture. This versatility
is gained at the cost of speed. As one will see in the next section,
Myricom has ported MPICH its performance far exceeds that of MPICH
using ethernet. GAMMA and VIA have also released ports to MPICH, all
of which are signs of MPICH's versatility. LAM performed better on
Astrolab, because it seems to be more suited for the Beowulf cluster
architecture, already.
Figure 1: Scaled Performance
All of the runs were scaled by dividing the Mflop/s/timestep by the the Mhertz clock speed.
Note: The last point for the Astrolab cluster using pgcc with MPICH is suspicious. We were unable to rerun the test on 16 nodes due to system complications. (postscript)
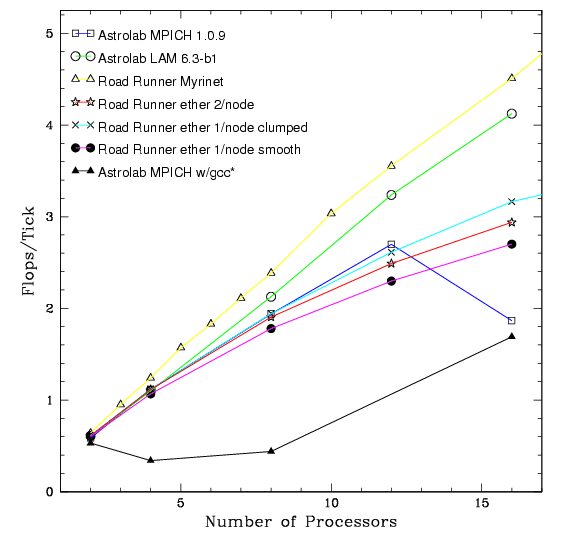
Figure 2: Raw Performance
This graph is a representation of the output of the Mflop/s/timestep. The division in the two starting points for each group of lines corresponding to the two different clusters is indicative of their having different processor speeds. (postscript)
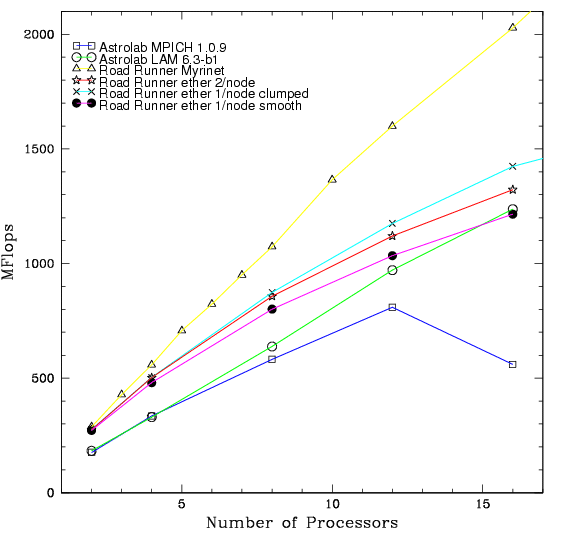
Figure 3: Science Rate
The science rate is defined as the number of particles computed per second. This is a robust benchmark, because one can compare two different architectures, which is not possible with the Mflop output. (postscript)

Myrinet and MPICH Performance on Road Runner
We performed four sets of runs; two using ethernet and the highly
evolved distribution (one process per node and two processes per
node), two using Myrinet (one with the highly evolved distribution and
one with a smooth distribution. In this section we present results
from the tests performed on the Roadrunner cluster and compare them to
the results of the tests on the Astrolab cluster. First, we compare
the results of the MPICH runs on Astrolab to those on Roadrunner. We
then compare the one process per node performance to the two process
per node performance. Thirdly, we examine the speed gained by using
the Myrinet message passing layer, and lastly, we compare a run using
a smooth distribution to that
of one using the highly evolved
distribution. The results from all of these tests are presented
in figures 1, 2, & 3.
The set of runs testing the performance of PKDGRAV on Roadrunner using
one process per node (the Roadrunner cluster has two 450Mhz processors
per node) produced a slightly worse scaling than it's counterpart on
Astrolab (fig 1). What this
indicates, is that PKDGRAV on a message passing machine is not as
dominated by memory latency. This is shown here by the fact that the
Astrolab performed slightly better than the Roadrunner cluster, which
has faster memory access. This conclusion needs more investigation,
mainly due the fact that the 16 node test on Astrolab is flawed.
In comparing the two ethernet runs using the highly evolved or clumped
distribution on Roadrunner, the one process/node sets perform better
than the two processes/node sets. This can be seen clearly in all
three figures 1, 2, & 3.
This is consistent with the comparison with the Astrolab. The
additional process on each node increases the load on the memory
subsystem, decreasing the overall performance. However, it could be
that having a free processor per node allows communication to be
handled separately from computations.
We tested PKDGRAV using Myrinet with a less evolved (smooth)
distribution in order to compare it with the set of tests done using
the highly evolved distribution. This allowed us to see how the
scaling and efficiency of the domain decomposition of PKDGRAV changed
over the time of a simulation. In figures 1 & 2 one
can see that the Mflops/sec for the clumped distribution is higher
than that for the smooth distribution. If one looks at figure 3, the scientific rate is much higher for
the smooth case. The discrepancy lies in the fact that the smooth
case is effected more by the memory and network latency. For each
particle force calculation less floating point operations are
performed, which means the processor is waiting more for information
to process causing the Mflop rate to decrease, but the scientific rate
is still higher as one would expect.

Perlinear Performance
The perlinear performance test examines the percent deviation from the
ideal case. The ideal case being a linear speed up directly
proportional to the number of nodes, in other words an instant
retrieval of information controlled by other processes. As one
expects, the faster the net connection, the better the perlinear
performance. As one can see in figure 4, the test runs on the Roadrunner
cluster using Myrinet experience only a 12% drop on 16 nodes from 2
node performance, compared to a 25% drop using ethernet. The greatest
advancement seen here is the perlinear performance of LAM using
ethernet on the Astrolab cluster compared to the performance of MPICH
on both clusters. LAM only experiences a 15-16% drop in performance
on 16 nodes, this combined with it's scaled performance makes it the clear
choice for MPI implementations on Beowulf class clusters with
commodity networking thus far in
our research. One promising aspect for the validity of figure 4 is
the constancy for which MPICH performs on both the Astrolab cluster
and the Roadrunner cluster. They perform almost identically, which
needn't be the case, because the cluster are setup differently. This
supports the above argument of MPICH giving consistent, yet
slower performance across many architectures. Figures 5 & 6
give alternate views of the perlinear performance. Figure 5 shows the the perlinear science rate,
which varies slightly from the Mflop perlinear case for all tests with
the exception of the Myrinet tests. This is discussed in the next
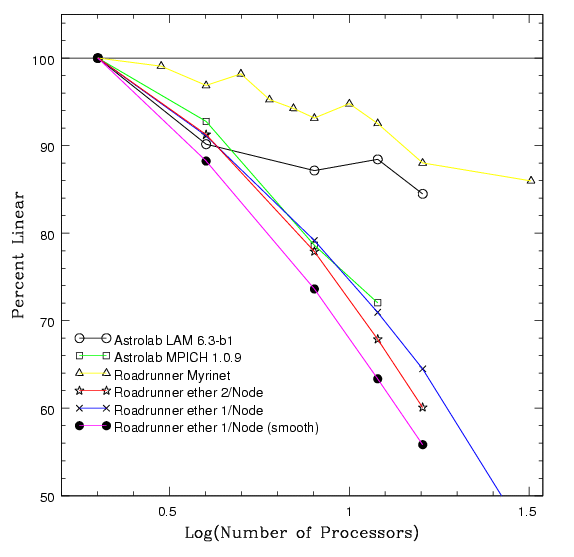
paragraph. Figure 6 is a log
plot of figure 4, which allows one to see further tests we conducted
using the Roadrunner cluster. On 32 nodes the Myrinet experienced
only a 14% drop in performance, compared to a 55% drop for the
ethernet performance.
While performing the tests, we first just tested 2, 4, 8, 12, & 16
nodes, and noticed in the perlinear plots that the performance on 12
nodes deviated consistently from the trend of the power of two node
performance. We further investigated this by performing more runs on
a different numbers of nodes using Myrinet. The performance on the
number of nodes which are not powers of two performed
consistently better (fig 4). This
performance difference is a direct effect of the domain decomposition
algorithm used by PKDGRAV, which is described in the PKDGRAV section. Because the
domain decomposition tends to divide the densest region in half when the
number of nodes is a power of two, the force calculations involve the
opening of more nodes on other processors. This means more message
passing and slower performance due to network latency. With non-powers of
two nodes the division is not made directly through the densest region.
The region is split into, e.g., threes and fives instead of two, which quite
often leaves the majority of the densest region on one node, therefore
reducing the communication needed. In the current case, the five node
performance showed the greatest improvement from the power of two
performance. What appears to be a super linear speed-up in science rate is due the fact that the
percent linear tests are being based upon a two node performance and
from what we have just stated one should expect a much better
performance from higher numbers of nodes. The message passing
increases with the number of nodes and that ultimately pushes the
performance back down. This effect is highly dependent on the
distribution and will therefore not always be the same, but if there
exists a region in a simulation that is much denser than the rest, one
should see such effects with the current domain decomposition algorithm.
This behavior is specific of the algorithm and we expect to also see
this with different MPI implementations.
Figure 4: Perlinear Scaling
The perlinear scaling shows the percent deviation from two processor performance. The two processor test was used as a base, because the memory required for a 1.3 million particle simulation exceeds the memory one machine in the Astrolab cluster. This graph is based on the Raw Mflops/sec performance test. (postscript)
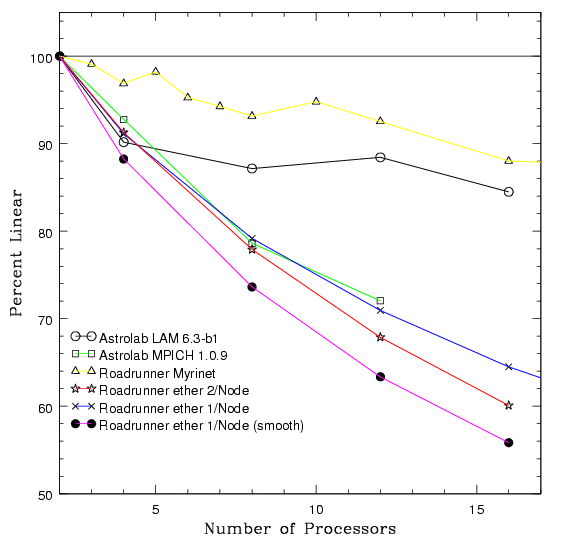
Figure 5: Perlinear Science Rate Scaling
The perlinear scaling shows the percent deviation from two processor performance. The two processor test was used as a base, because the memory required for a 1.3 million particle simulation exceeds the memory one machine in the Astrolab cluster. This graph is based on the Science Rate performance test. (postscript)
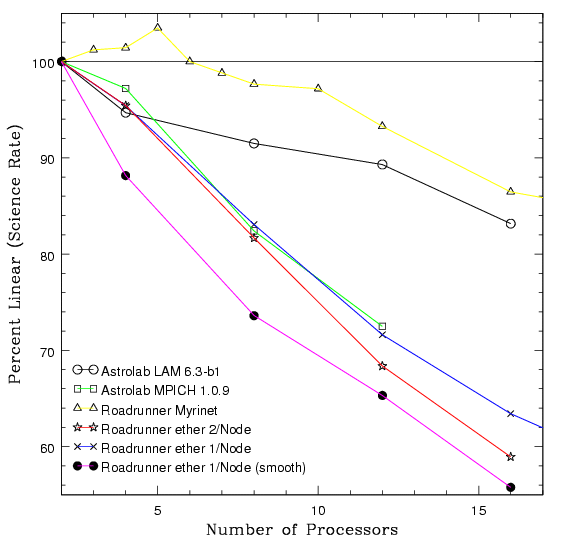
Figure 6: Perlinear (Log) Scaling
The perlinear scaling shows the percent deviation from two processor performance. The two processor test was used as a base, because the memory required for a 1.3 million particle simulation exceeds the memory one machine in the Astrolab cluster. This graph is based on the Raw Mflops/sec performance test. (postscript)

Conclusion
In this paper we have presented the performance test results of
PKDGRAV using different MPI implementations on two Beowulf class
clusters. This investigation will soon be followed up with an
investigation of GAMMA and VIA passing layers. We found that
although Myrinet performs much better than ethernet over all with
PKDGRAV, the LAM implementation of MPI over ethernet performs the best
for the cost on Beowulf styles clusters like those covered in this
investigation. We also found that the performance lost by using dual
processor nodes instead of single processor nodes is not very
significant; therefore, it may be advantageous in terms of Mflops per
dollar to construct Beowulf clusters with dual processor nodes.
Finally, the information collected regarding the domain decomposition
will be using in a new domain decomposition algorithm that will attempt
to optimize the decomposition in a similar way to that used by a chess
game, by testing a few different configurations before deciding on
one. The time it takes to do this determination will be over come by
the reduction of communication needed.

 MPICH and LAM Performance on Astrolab
MPICH and LAM Performance on Astrolab Figure 1: Scaled Performance
Figure 1: Scaled Performance Figure 2: Raw Performance
Figure 2: Raw Performance Figure 3: Science Rate
Figure 3: Science Rate Myrinet and ethernet Performance on Road Runner
Myrinet and ethernet Performance on Road Runner Perlinear Performance
Perlinear Performance Figure 4: Perlinear Scaling
Figure 4: Perlinear Scaling Figure 5: Perlinear Science Rate
Figure 5: Perlinear Science Rate Figure 6: Perlinear (log) Scaling
Figure 6: Perlinear (log) Scaling Conclusion
Conclusion





