PKDGRAV (Parallel K-D tree GRAVity code)

The following is an adaptation of a previous paper written by Marios D. Dikaiakos and Joachim Stadel¹. The changes made are both stylistic (i.e footnotes) and reflect the improvements made in PKDGRAV.

The k-D Tree Structure
Calculating Gravity

Periodic Boundary Conditions

Parallel Aspects of the Code

Domain Decomposition
Parallel tree-walking phase
The Machine Dependent Layer

The k-D Tree Structure

The central data structure in PKDGRAV is a tree structure which forms the hierarchical representation of the mass distribution. Unlike the more traditional oct-tree used in the Barnes-Hut algorithm, we use a k-D tree², which is a binary tree. The root-cell of this tree represents the entire simulation volume. Other cells represent rectangular sub-volumes that contain the mass, center-of-mass, and moments up to hexadecapole order of their enclosed regions.

To build the k-D tree, we start from the root-cell and bisect recursively the cells through their longest axis. At the very top of the tree we are domain decomposing among the processors, so the bisection is done such that each processor gets an equal computational load. The computational cost is calculated from the previous timestep. Once we are within a processor, each cell is bisected so that the sub-volumes are of equal size so that higher order moments of cells are kept to a minimum (Figure 1). The depth of the tree is chosen so that we end up with at most 8 particles in the leaf cells (buckets). We have found this number to be near optimal for the parallel gravity calculation.

**Figure 1:** Two-dimensional k-D Tree distributed over four processors.
$\begin{figure}\centerline{\psfig{figure=FIGS/kDT.ps,width=4in}} \end{figure}$

Several factors motivated the use of k-D tree structure over the classical oct-tree. The simplicity of the structure allows for a very efficient tree-construction. The use of buckets, by which only $2 \lceil N/8 \rceil$ nodes are required, makes the tree structure memory-efficient. Most significantly, it can be extended to a parallel, distributed tree structure in a very natural way.

Calculating Gravity

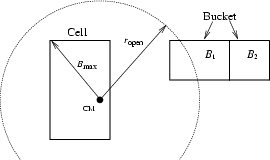
PKDGRAV calculates the gravitational accelerations using the well known tree-walking procedure of the Barnes-Hut algorithm³, except that it collects interactions for entire buckets rather than single particles. Thus, it amortizes the cost of tree traversal for a bucket, over all its particles. In the tree building phase, PKDGRAV assigns to each cell of the tree an opening radius about its center-of-mass. This is defined as,

$\begin{displaymath}r_{\rm open} = {2 B_{\rm max} \over \sqrt{3} \; \theta} + B_{\rm center} \end{displaymath}$

(1)

where $B_{\rm max}$ and $B_{\rm center}$ are the maximum distances from a particle in the cell to the center-of-mass and center-of-cell respectively. $\theta$ is a user specified accuracy parameter which is similar to the traditional $\theta$ parameter of the Barnes-Hut code; notice that decreasing $\theta$ in Equation 1, increases $r_{\rm open}$ .

The opening radii are used in the Walk phase of the algorithm as follows: for each bucket ${\cal B}_i$ , PKDGRAV starts descending the k-D tree, ``opening'' those cells whose $r_{\rm open}$ intersect with ${\cal B}_i$ (Figure 2). If a cell is ``opened,'' then PKDGRAV repeats the intersection-test with ${\cal B}_i$ for the cell's children. Otherwise, the cell is added to the particle-cell interaction list of ${\cal B}_i$ . When PKDGRAV reaches the leaves of the tree and a bucket ${\cal B}_j$ is opened, all of ${\cal B}_j$ 's particles are added to the particle-particle interaction list of ${\cal B}_i$ .

**Figure 2:** Opening radius for a cell in the k-D tree, intersecting bucket B₁ and not bucket B₂. This cell is ``opened'' when walking the tree for B₁. When walking the tree for B₂, the cell will be added to the particle-cell interaction list of B₂.
$\begin{figure}\centerline{\psfig{figure=FIGS/oprad.ps,width=2.4in}} \end{figure}$

Once the tree has been traversed in this manner we can calculate the gravitational acceleration for each particle of ${\cal B}_i$ by evaluating the interactions specified in the two lists. PKDGRAV uses a fourth-order multipole expansion to calculate particle-cell interactions.

Periodic Boundary Conditions

One disadvantage of tree codes is that they must deal with periodic boundary conditions explicitly, unlike grid codes where this aspect is taken care of implicitly. Although this adds complexity to any tree code, it is possible to incorporate periodic boundary conditions efficiently by using approximations to the Ewald summation technique^4,5. PKDGRAV differs significantly from the prescription given by [4], which is ill suited to a parallel code. Due to the mathematical technicality of the method we do not provide further description here except stating that it is ideally suited to parallel computation⁶.

Parallel Aspects of the Code

Domain Decomposition

Achieving effective parallelism requires that work be divided equally amongst the processors in a way which minimizes interprocessor communication during the gravity calculation. Since we only need a crude representation for distant mass, the concept of data locality translates directly into spatial locality within the simulation. Each particle can be assigned a work-factor, proportional to the cost of calculating its gravitational acceleration in the prior time-step. Therefore, during domain decomposition, we divide the particles into spatially local regions of approximately equal work.

Experience has shown that using a data structure for the domain decomposition that does not coincide with the hierarchical tree for gravity calculation, leads to poor memory scaling with number of processors and/or tedious book-keeping. That is the case, for instance, when using an Orthogonal Recursive Bisection (ORB) tree for domain decomposition and an oct-tree for gravity⁷. Current domain decomposition techniques for the oct-tree case involve forming ``costzones,'' that is, processor domains out of localized sets of oct-tree cells⁸, or ``hashed oct-trees''⁹. PKDGRAV uses the ORB tree structure to represent the domain decomposition of the simulation volume. The ORB structure is completely compatible with the k-D tree structure used for the gravity calculation (Figure 1). A root finder is used to recursively subdivide the simulation volume so that the sums of the work-factors in each processor domain are equal. Once this has been done, each processor builds a local tree from the particles within its domain. This entire domain decomposition and tree building process is fully parallelizable and incur negligible cost to the overall gravity calculation.

Parallel tree-walking phase

The Walk phase starts from the root-cell of the domain decomposition tree (ORB tree), each processor having a local copy of this tree, and descends from its leaf-cells into the local trees stored on each processor. PKDGRAV can index the parent, sibling and children of a cell. Therefore, it can traverse a k-D tree stored on another processor in an architecture independent way. Non-local cells are identified uniquely by their cell index and their domain number (or processor identifier). Hence, tree walking the distributed data structure is identical to tree walking on a single processor, except that PKDGRAV needs to keep track of the domain number of the local tree upon which the walk is performed. Interaction lists are evaluated as described earlier, making Walk the only phase where interprocessor communication takes place, after the domain decomposition.

The Machine Dependent Layer

A small library of high level functions called MDL (Machine Dependent Layer) handles all parallel aspects of the code. This keeps the main gravity code architecture-independent and simplifies porting. For example, MDL provides a memory swapping primitive to move particles between processors during domain decomposition. Furthermore, MDL provides memory sharing primitives allowing local arrays of data to be visible to all processors. These primitives support access to non-local cells and particles during the Walk phase. In particular, a procedure called mdlAquire can be used to request and receive non-local data by providing an index into a non-local array, and an identifier for the processor that owns that array. On shared address space machines, we rely on the shared address space to implement mdlAquire.

On distributed memory machines, such as workstation clusters and IBM's SP-2, we maintain a local software cache on each processor. When a processor requests a cell or particle that is not in its cache, the request is sent to the appropriate processor that owns the data. While waiting for the data to be sent back, the requesting processor handles cache-requests sent from other processors. The owner processor sends back a cache line comprised of more than a single cell or particle, in an attempt to amortize the effects of latency and message passing overhead. This cache line is inserted into the local cache, and a pointer to the requested element is returned. To improve responsiveness of the software cache, after a number of accesses to the cache MDL checks whether any requests for data have arrived; if so, it services these first.