Final project

Due Thursday, June 9, 2011, by 11:00pm PDT, by pushing to your bitbucket repository.

The goals of this project are to

• Gain some experience with writing Python scripts.
• Gain some more experience with OpenMP and MPI.

Make sure you update your clone of the class repository before doing this assignment:

$ cd $CLASSHG
$ hg pull -u     # pulls and updates

You should also create a directory $MYHG/homeworks/project to work in since this is where your modified versions of the files will eventually need to be.

The directory $CLASSHG/codes/python/quadrature_convergence contains a variant of the code from Homework 4 to test the Trapezoid method and Simpson’s method for quadrature.

The main program is now in the file runquad.f90 and requires that the value of n be in a file input.txt. It uses both methods and prints the resulting errors, along with the value of dx for this n, in the file output.txt.

This directory also contains a file quadtests.py that defines a Python module with a function run_tests. This function has an optional argument that is a list of n values to test. For each n it creates a file input.txt, runs the code using the os.system function, and then reads in the resulting errors, collecting them in arrays. The module also has a function plot_errors that can be used to produce plots of the results.

In lecture on June 6 this will be discussed in more detail.

The project concerns modifying this code to test the Trapezoid rule in two space dimensions for the approximation of an integral of the form

I = \int_a^b \int_c^d g(x,y) \, dy \, dx

This can be rewritten as \int_a^b f(x) \, dx where the function f(x) = \int_c^d g(x,y) \, dy.

We can approximate the integral of f(x) by the trapezoid rule in x. For each x we must approximate f(x) by a trapezoid rule approximation to the integral of g(x,y) in y.

Suppose we use nx cells in x and ny cells in y, and let

\Delta x = (b-a)/nx, \qquad \Delta y = (d-c)/ny

and define points where we will evaluate functions using

x_i = a + (i-1)\Delta x, \qquad i=1, 2, \ldots, nx+1

y_j = c + (j-1)\Delta y, \qquad j=1, 2, \ldots, ny+1.

Then the two-dimensional integral can be approximated by

I \approx \frac 1 2 \Delta x \sum_{i=1}^{nx+1} (f(x_i) + f(x_{i+1})) = \frac 1 2 \Delta x (f(a) + f(b)) + \Delta x \sum_{i=2}^{nx} f(x_i).

But now for each $i$ we must approximate f(x_i) by

f(x_i) \approx \frac 1 2 \Delta y \sum_{i=1}^{ny+1} (g(x_i,y_j) + g(x_i,y_{j+1})) = \frac 1 2 \Delta y (g(x_i,c) + g(x_i,d)) + \Delta y \sum_{i=2}^{ny} g(x_i,y_j).

Inserting this in the above sum, we see that the double integral I is now approximated by a double sum.

Part A

Write a serial program structured similar to the one in $CLASSHG/codes/python/quadrature_convergence to approximate a double integral using the Trapezoid Rule as described above. Your directory $MYHG/project/parta should contain the following:

• A module functions_mod.f90 that defines the function g(x,y) to be integrated. You do not need to specify an indefinite integral function. Instead you can simply specify the true solution in your main program for the problem you are solving.

• A module quadrature_mod.f90 that contains a function trapezoid with signature:

  subroutine trapezoidal(g, a, b, c, d, nx, ny, integral)

  This subroutine should compute the double integral and return this value.

  You may find it convenient to define an allocatable local array in this subroutine to hold values of the one dimensional integrals f(x_i) that you will compute for each x_i. Or you can simply sum things in a double loop, but be careful about the weights at each point around the boundary!

• A main program runquad.f90 that does the following:

  • Reads nx, ny from input.txt. Assume both integers are on a single line in the file, separated by white space.
  • Calls trapezoid and then computes the error in the value returned.
  • Prints dx, dy, error on a single line to a file output.txt.
  • Prints out the number of times the integrand function was evaluated, which should be (nx+1) * (ny+1) if you’ve implemented it well.

• A Makefile so that make run will run the code.

Test your program with several case for which you can compute the exact integral for comparison. For the version you turn in, use the function

g(x,y) = \sin(x)\sin(y)

and approximate the integral

\int_0^\pi \int_0^{\pi/2} g(x,y) \, dy\, dx = 2

• Your directory for Part A should also contain a Python module quadtest.py containing

  • a function run_tests(nxlist, nylist) that runs the code for a sequence of values (nx,ny) taken from these lists, reads in the resulting values in output.txt, and returns the tuple (dx,dy,errors) where each of these is an array of the same length as nxlist and nylist.
  • a function plot_errors(dx,dy,errors) that produces a log-log plot of abs(error) versus max(dx,dy).
  • a “main program” so that if the the module is executed as a script it will execute both functions (see $CLASSHG/codes/python/quadrature_convergence/quadtest.py for an example)

If you code is working, you should observe second order accuracy. For example, with the test problem suggested above, it might be reasonable to use

• nxlist = [10, 20, 40, 80]
• nylist = [5, 10, 20, 40]

and you should then obtain a plot like this:

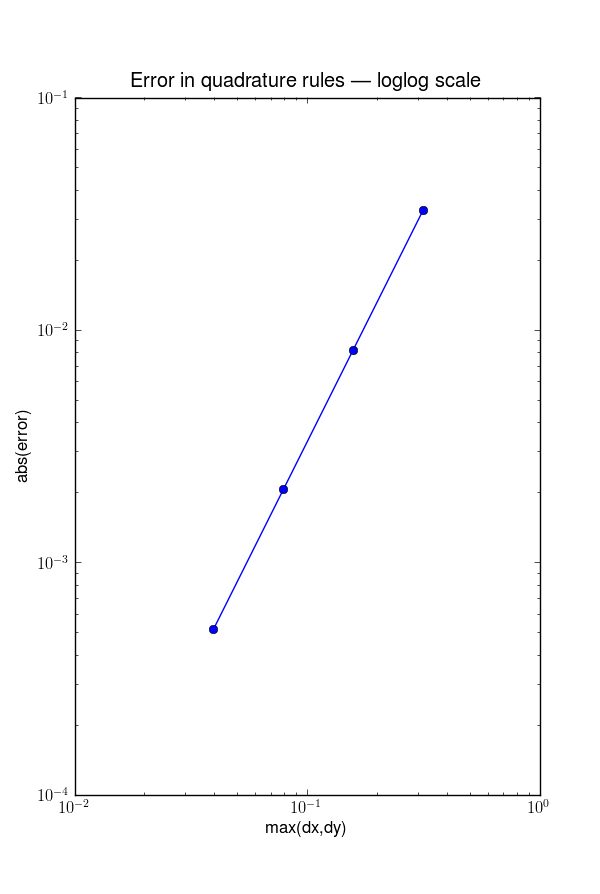
If you only observer first order accuracy (if the error is proportional to dx rather than to dx**2) then there is a bug in your code.

Part B

Modify your code to use OpenMP to compute the double sum, using “fine grain” parallelism. Replace the outer loop by a parallel do loop. You will also have to add a reduction to compute the final integral.

The main program should read the number of threads to use from a file nthreads.txt that contains a single integer. This value can be stored in a module variable nthreads of the quadrature_mod so that it is available in the trapezoidal subroutine.

The signature of the trapezoidal subroutine should be the same as in Part A.

Have the code print out which values of i each thread is handling. The code should work for any number of threads, and should also run if compiled without the -fopenmp flag.

Have the main program print out at the end how many function evaluations were done by each thread. Remember that the function evaluation counter will now have to be an array. Also print out the total number of function evaluations.

Confirm that you get the same results with this version of the code.

Part C

Modify your code from Part A to use MPI. Split up the values of i between processes and have each process compute part of the integral.

Note that the processes do not have to exchange the data as was necessary for the Jacobi iteration, so this should be easier to do than Homework 6. You will need to do a reduction to compute the final integral.

Have the trapezoidal subroutine print out which values of i each process is handling. The code should work for two or more processes.

Have the main program print out at the end how many function evaluations were done by each process. Also print out the total number of function evaluations. Note that this will require another reduction.

The signature of the trapezoidal subroutine should be the same as in Part A.

Confirm that you get the same results with this version of the code.

What to turn in

The directories project/parta, project/partb, and project/partc should each contain:

• Fortran codes
• A Makefile that works for the fortran codes, that allows you to type make run to run the code.

The directory project/parta should also contain a file quadtest.py. You don’t need to include this file in the other directories, although the other versions should use input and output files in the same way so that this same module could be used to plot results from any of the versions.

When you are done, don’t forget to use the hg add, hg commit, and hg push commands to push these to your bitbucket repository for grading.