Homework 6

Due Thursday, May 26, 2011, by 11:00pm PDT, by pushing to your bitbucket repository.

The goals of this homework are to

• Better understand Jacobi iteration
• Gain some experience with MPI.

Make sure you update your clone of the class repository before doing this assignment:

$ cd $CLASSHG
$ hg pull -u     # pulls and updates

You should also create a directory $MYHG/homeworks/homework6 to work in since this is where your modified versions of the files will eventually need to be.

See

• MPI
• MPI with subroutine calls
• Slides from lectures for Lectures 18-23

The directory $CLASSHG/codes/fortran/heat2d contains main program and subroutine that together solve a two-dimensional steady state heat conduction problem by Jacobi iteration. The problem is the Poisson problem

u_{xx} + u_{yy} = f(x,y)

on the unit square 0\leq x\leq 1, 0\leq y\leq 1 with boundary conditions that specify the values of u at all points around the boundary. The equations are solved on an n \times n Cartesian grid with n^2 interior points (the grid points are indexed from 0 to n+1 in each direction with the first and last being boundary points where the values are specified). The grid points are equally spaced with \Delta x = \Delta y = h.

The code is currently set to solve the above problem with f(x,y) = 0 and boundary values

Left boundary:

u(x,y) = 0 for x=0 and 0\leq y \leq 1

Right boundary:

u(x,y) = \left\{ \begin{array}{ll} 1&~~x=1, ~0.3<y<0.7\\ 0&~~ x=1, (y\leq 0.3 ~\text{or}~ y\geq 0.7) \end{array}\right.

Bottom boundary:

u(x,y) = 0 for y=0 and 0\leq x \leq 1

Top boundary:

u(x,y) = \left\{ \begin{array}{ll} 1&~~y=1, ~0.3<x<0.7\\ 0&~~ y=1, (x\leq 0.3 ~\text{or}~ x\geq 0.7) \end{array}\right.

With these boundary conditions the temperature is held at 0 all around the boundary except for two hot spots along the top and right boundary. The resulting temperature distribution is shown in the figures below both as a pseudocolor plot and as a contour plot.

Assignment:

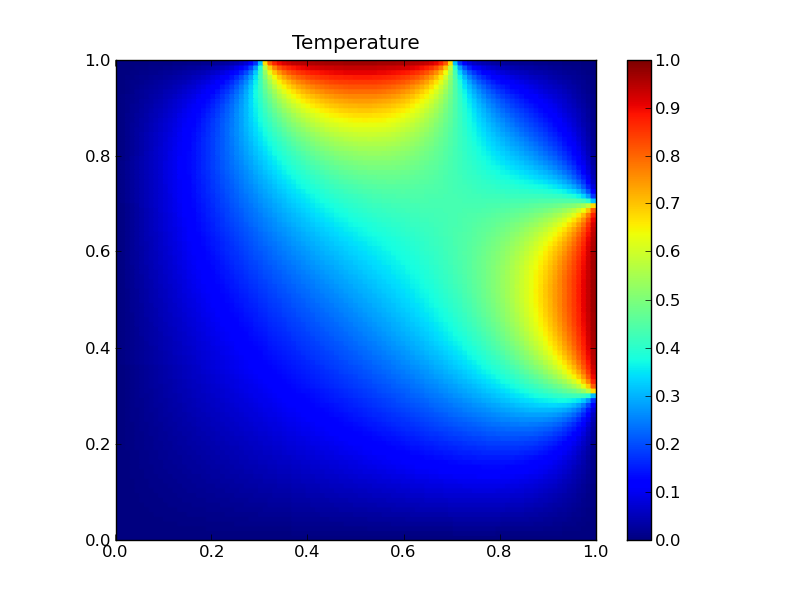
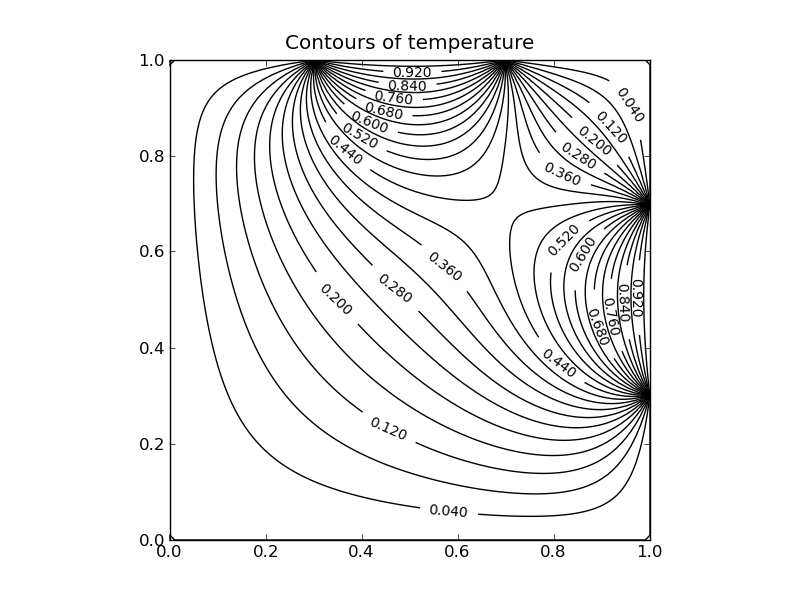
The assignment is to convert this code into an MPI version.

• Create a subdirectory $MYHG/homeworks/homework6 to contain an MPI version of the two-dimensional Jacobi solver. It should contain:

  • jacobi2d_main_mpi.f90
  • jacobi2d_sub_mpi.f90
  • Makefile
  • readme.txt

  This code should solve the same problem as implemented in $CLASSHG/codes/fortran/heat2d

• Typing:

  make plots

  should produce plots such as those shown above. For this you can use the python script in $CLASSHG/codes/python/plotheat2d.py. See $CLASSHG/codes/fortran/heat2d/Makefile for the rule used to make plots.

• Use the form of the code in $CLASSHG/codes/mpi/heat1d a model for structuring this code. This is a version of Jacobi iteration in 1 dimension that uses a main program and a subroutine, and solves the same problem as the code in $CLASSHG/codes/mpi/jacobi2_mpi.f90 where the implementation was done in a single program.

  See MPI with subroutine calls for some discussion of the use of MPI with subroutine calls and how it differs from what might be done with OpenMP.

  Your code should run with the main program and subroutine you provide, and you should modify the Makefile as needed and provide a readme.txt file with instructions on how to use it.

  Your subroutine should also work if it is called from a different main program (with the correct calling sequence), as we might do in grading this assignment.

• In two dimensions you will have to specify how to split the i,j values between processes. Do this by splitting up the values j=1,n into chunks from j=jstart,jend (as in one dimension) with each process handling all values of i=1,n within its own set of j values. In other words, a 12 x 12 grid would be split among 4 processes as indicated below:

  

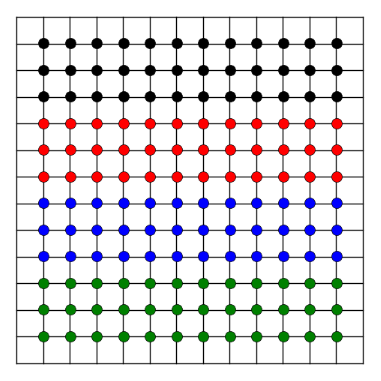
  Note that each iteration you should use MPI_ISEND and MPI_RCV to transfer information at the edges of each chunk to the neighboring processes.

  The values that must be sent should be contiguous in memory when the grid is split into horizontal strips. Note that grid indexing is different than matrix indexing! Horizontal rows of a grid correspond to elements u(i,j) with i varying and j fixed, the same as a column of a matrix.

• When you are done, don’t forget to use the hg add, hg commit, and hg push commands to push these to your bitbucket repository for grading.