Table Of Contents

Convergence Acceleration
- Examples

Previous topic

Next topic

This Page

Convergence Acceleration¶

We consider various convergence acceleration techniques in the module mmf.math.integrate.acceleration. These are useful for accelerating series (i.e. if you are trying to sum an infinite number of terms than fall off smoothly) or extrapolating quantities to an infinite limit.

Examples¶

As an example and a test of the messages, we will compute a lattice sum of a radially spherical function in two dimensions:

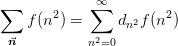
$\sum_{\vect{n}} f(n^2) = \sum_{n^2=0}^{\infty} d_{n^2}f(n^2)$

where $d_{n^2}$ is the degeneracy factor. In two dimensions this is easy to compute as follows: