mmf.math.integrate.acceleration¶
| levin(s[, type, k0, degree, ds]) | Return the triangular acceleration table a for n terms of |
This module provides some techniques for sequence acceleration.
Most of the theory and notation follows D. Laurie’s discussion in Appendix A. of [R4]. The general model is that the sequence has the form:
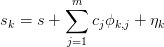
where  is the converged result,
is the converged result,  is some set
of known residual dependencies with unknown coefficients
is some set
of known residual dependencies with unknown coefficients 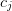 and
and 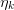 is a residual that will be taken to be negligible
[R3].
is a residual that will be taken to be negligible
[R3].
The acceleration will be summarized in a table of coefficients
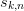 as follows:
as follows:

where the arrows show the dependencies: Each term 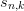 is a
function of the terms
is a
function of the terms 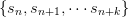 . The
first column is thus the original sequence.
. The
first column is thus the original sequence.
Linear Accelerations¶
Here we consider linear sequence transformations  such that
such that
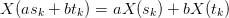 . In particular, we
consider each column of
. In particular, we
consider each column of 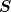 to be a linear transformation
of the previous column:
to be a linear transformation
of the previous column: 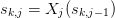 . In this
case, we may provide an explicit construction using n terms that
eliminates the first n residuals by demanding:
. In this
case, we may provide an explicit construction using n terms that
eliminates the first n residuals by demanding:
(1)![\begin{aligned}
s_{k+\delta} &= s_{k,n} + \sum_{j=1}^{n}c_{j}\phi_{k+\delta,j}, &
\delta &\in[0,1,\cdots,n].
\end{aligned}](../../../_images/math/a7ddcb0b154a59781aa54709d744145f290aff4e.png)
This defines the entry 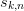 in terms of the original
elements of the sequence below and to the left by defining
in terms of the original
elements of the sequence below and to the left by defining 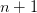 equations for the
equations for the 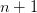 unknowns
unknowns 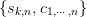 . Note that for each
. Note that for each 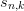 , the set of
coefficients
, the set of
coefficients  is different because this is not the
original sequence (for example, we have truncated and ignored the
error terms
is different because this is not the
original sequence (for example, we have truncated and ignored the
error terms  ).
).
Naively, one may directly solve these systems of equations for each of
entries 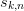 , but this takes
, but this takes 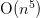 operations. There is a general procedure called the “E-algorithm”
that reduces this to
operations. There is a general procedure called the “E-algorithm”
that reduces this to 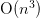 which we now present. This
is implemented by e_algorithm(). For special forms of the
residuals
which we now present. This
is implemented by e_algorithm(). For special forms of the
residuals  specialized methods exist which are often
much faster. Some of these are described later.
specialized methods exist which are often
much faster. Some of these are described later.
Note
For linear models, one should obtain convergence either proceeding down or to the right, but the key feature is that the convergence of the rows to the right should be much faster: this indicates that the underlying model is good. If the rows do not converge much faster than the columns, one should consider a different acceleration technique.
General E-Algorithm¶
As we discussed above, each successive column of S may be expressed
in terms of this as an affine combination of the previous two entries
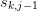 and
and 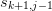 :
:
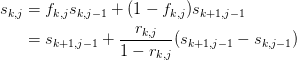
(The affinity is required to preserve the linearity, for example, so
that 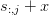 and
and 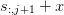 converge to the
same value
converge to the
same value 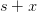 .)
.)
Start with the original sequence 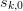 as the first column
of
as the first column
of 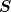 . Consider this, along with the new sequence
. Consider this, along with the new sequence
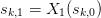 and the sequence of residuals
and the sequence of residuals
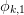 . The transformation
. The transformation  can be represented
as a matrix:
can be represented
as a matrix:
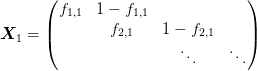
Equations (1) for  are then satisfied if
are then satisfied if
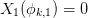 which defines the coefficients:
which defines the coefficients:
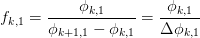
The E-algorithm is then to apply this transformation 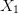 to
the rest of the columns of
to
the rest of the columns of  to obtain a new set of
residuals (the first column having been annihilated). Now treat
to obtain a new set of
residuals (the first column having been annihilated). Now treat
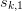 as the new original sequence and repeat the process.
This is implemented by e_algorithm(). In certain special cases,
one can directly derive formula for the coefficients
as the new original sequence and repeat the process.
This is implemented by e_algorithm(). In certain special cases,
one can directly derive formula for the coefficients 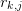 .
The table
.
The table 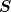 can them be directly constructed. This is
done in direct_algorithm().
can them be directly constructed. This is
done in direct_algorithm().
To estimate the error-sensitivity, we consider each entry
 to be a function of the
original sequence entries. Given errors in the input
to be a function of the
original sequence entries. Given errors in the input 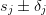 , an estimate of the error in the result is
, an estimate of the error in the result is
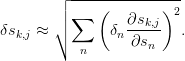
For linear algorithms, this is easy to compute since ![s_{k,j} =
\left[\mat{K}_{j}\cdot \vect{s}\right]_k](../../../_images/math/afbb70120df949a1f3e3dcd87863576136e5c0be.png) where
where 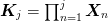 . The squares of the errors
. The squares of the errors 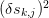 will be the diagonals of the matrix
will be the diagonals of the matrix
 .
.
For some of the faster specialized algorithms, it is a bit cumbersome to compute this exactly, so we directly propagate the errors as either

or
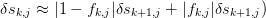
This will overestimate the errors as cancellations that occur at various stages are not taken into account, but in practise, this is not very significant.
Richardson Extrapolation¶
The Richardson extrapolation method considers models of the form
(2)
These most typically arise in problems such as differentiation,
integration, or discretization where there is a step-size 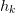 that is decreased at successive stages. The most general model
(2) requires the full E-algorithm, but there are several
special cases that admit analytic solutions:
that is decreased at successive stages. The most general model
(2) requires the full E-algorithm, but there are several
special cases that admit analytic solutions:
Geometric progression of step sizes with constant r:
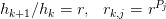
Arithmetic progression of exponents:
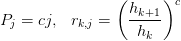
Modified Salzer’s Extrapolation¶
The modified Salzer’s extrapolation is based on a model of the form

This provides another efficient method which can be derived by
dividing (1) by  :
:
![\begin{aligned}
\frac{s_{k+\delta}}{\psi_{k+\delta}} &=
\frac{s_{k,n}}{\psi_{k+\delta}} + \sum_{j=0}^{n-1}
\frac{c_{j+1}}{(k+\delta+k_{0})^j}, &
\delta \in [0,1,\cdots,n].
\end{aligned}](../../../_images/math/0e6d403c58d5620a1f89647bc53e84926fbcc23b.png)
From this we can construct the solution in terms of the divided
difference operators 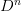 : at
: at  which acts as
a difference of the sequence
which acts as
a difference of the sequence 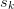 as a function of
as a function of 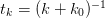 . The idea here is that the sum on the right is a
polynomial of order
. The idea here is that the sum on the right is a
polynomial of order  in t_k, and hence will be
annihilated by the n th difference operator at
in t_k, and hence will be
annihilated by the n th difference operator at  .
.

Semi-linear Accelerations¶
The previous linear acceleration techniques are fairly robust, and one can generally prove that if the original sequence converges, then the accelerated sequence will also converge to the same limit. However, to obtain convergence, one must put good inputs into the model (1).
Perhaps the most famous of these methods are those due to Levin.
These are generalizations of the Salzer expansion where the function
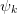 is expressed in terms of the residuals
is expressed in terms of the residuals 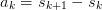 of the sequence (as opposed to linear methods where
of the sequence (as opposed to linear methods where
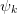 is determined a priori independently of the actual
sequence). Semi-linear methods often work well, even if no a priori
information about the sequence is know, however, they are also more
difficult to characterize. (For example, even if the transformation
is exact for two sequences, it may not be exact for them sum as the
transformations are not completely linear.)
is determined a priori independently of the actual
sequence). Semi-linear methods often work well, even if no a priori
information about the sequence is know, however, they are also more
difficult to characterize. (For example, even if the transformation
is exact for two sequences, it may not be exact for them sum as the
transformations are not completely linear.)
To understand where the Levin transformation works, note that

The three most common Levin accelerations are:
T: 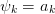
U: 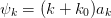
W: 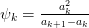
Notes and References¶
| [R3] | Determining the form of Instead, one must find a good set of approximation that fall off sufficiently rapidly which is why these types of sequences work well with Salzar’s modified algorithm. |
| [R4] | F. Bornemann, D. Laurie, S. Wagon, and J. Waldvogel, The SIAM 100-Digit Challenge: A Study in High-Accuracy Numerical Computing, SIAM, 2004. |
- mmf.math.integrate.acceleration.levin(s, type='u', k0=0, degree=None, ds=None)[source]¶
Return the triangular acceleration table a for n terms of the sequence s[k] using the Levin transformation type.
Parameters : s : 1-d array of length n
s[k] should be the k’th term in the sequence.
type : ‘t’, ‘u’, or ‘w’
Type ‘u’ is typically the most generally useful as it works whenever type ‘t’ works, however, ‘t’ works well for sequences
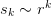 and usually requires one less term, so for
these types of sequences, it should be used to reduce roundoff
error. For types ‘t’ and ‘u’ the returned table
acceleration table a is (n-1 x n-1). For type w, the
table is (n-2 x n-2).
and usually requires one less term, so for
these types of sequences, it should be used to reduce roundoff
error. For types ‘t’ and ‘u’ the returned table
acceleration table a is (n-1 x n-1). For type w, the
table is (n-2 x n-2).k0 : float
Constant for the ‘u’ transform.
degree : int
Degree of extrapolation to use to determine last difference a_k
ds : None or float or 1-d array of length n
This should be an estimate of the errors in the terms of the sequence. If it is a single number, it is interpreted as the relative error in the terms, otherwise it is taken to be the array of absolute errors.
If it is not None, then the error estimate array dS will also be returned.
Returns : S : array (n x n)
Triangular acceleration array. The rows S[k,:] should converge faster than the columns S[:,n], otherwise the model should not be trusted. Without round-off error, S[0,-1] would be the best estimate, but at some point, round-off error becomes significant.
dS : array (n x n)
If ds is provided and not None, then this array of error estimates will also be returned.
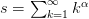 with partial sums
with partial sums 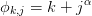 which will ultimately be exact. However, after
summing only n terms, the residual will still be
which will ultimately be exact. However, after
summing only n terms, the residual will still be ![\eta_{k}
= \sum_{j=2m}^{\infty}{k+j}^{\alpha} \approx
\order[(2m)^{\alpha+1}]](../../../_images/math/9e5d485c44b004a28ca415ec2b7d8bd785563250.png) which is certainly not negligible if the
series needs convergence acceleration!
which is certainly not negligible if the
series needs convergence acceleration!