mmf.solve.solver_utils¶
| IterationError | Iteration has failed for some reason. |
| NoDescentError | No downhill step could be found. |
| line_search(g, g0[, g1, trust_dg, ...]) | Return (l, g(l)) where g(l) decreases sufficiently. |
Inheritance diagram for mmf.solve.solver_utils:

Solver Utilities.
This module provides some utilities used by various solvers.
- class mmf.solve.solver_utils.IterationError¶
Bases: exceptions.Exception
Iteration has failed for some reason.
- __init__()¶
x.__init__(...) initializes x; see help(type(x)) for signature
- class mmf.solve.solver_utils.NoDescentError[source]¶
Bases: mmf.solve.solver_interface.IterationError
No downhill step could be found.
- __init__()¶
x.__init__(...) initializes x; see help(type(x)) for signature
- mmf.solve.solver_utils.line_search(g, g0, g1=None, trust_dg=False, allow_backstep=True, mesgs=Mesg(show=Container(info=False, status=True, warn=False, error=True, iter=False), store=Container(info=True, status=True, warn=True, error=True, iter=False)), max_steps=10, avg_descent_factor=0.0001, min_step=1e-05, min_scale_factor=0.1, max_scale_factor=0.5, use_cubic_factor=0.5, allow_bad_step=False)[source]¶
Return (l, g(l)) where g(l) decreases sufficiently.
The assumption idea here is that one is trying to minimize a function g(x) where x = x0 + l*dx and dx is known to be a local downhill direction. Taking a large step l=1 could work well if the function is linear, but if the function fluctuates on length scales comparable to |dx|, then one needs to take a shorter step.
The step size is monotonically reduced and a cubic interpolation scheme is used to find the optimal step using a minimal number of steps.
The standard line search algorithm can use this with g(l) = g(x0 + l*dx) but more general search algorithms can also be used.
Parameters : g : function
This should return the objective function g(l) where l is the scale parameter. l will monotonically decrease from 1.
g0 : float
Value of objective g(0) at l=0.
g1 : float (optional)
Value of objective g(1) at l=1.
trust_dg : bool, optional
If True, then we assume that the model for g(l) is correct (see below) and use
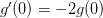 in order to perform
extrapolations for the optimal l. This will ensure l is
always positive. Otherwise, a quadratic approximation might be
used which allows for negative l.
in order to perform
extrapolations for the optimal l. This will ensure l is
always positive. Otherwise, a quadratic approximation might be
used which allows for negative l.allow_backstep : bool, optional
If True (default), then take the second step in the negative direction if not trust_dg. This may scale the problem in an inefficient manner, so we provide this option to suppress backsteps until some information is build up about the function.
mesgs : IMesg
Messages are displayed using this.
allow_bad_step : bool, optional
If True, then accept bad steps (i.e. do nothing other than compute new g(1).)
Other Parameters: avg_descent_factor : float
A successful step is one which decreases the objective function by at least this relative amount:
g < - g0*(1 - l*(2-l)*avg_descent_factor)
where we take l to be positive here. This prevents infinite loops.
Note
- This form is predicated on the assumption that
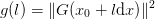
where
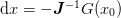 is the Newton step. If
this is the case, then for a linear function
is the Newton step. If
this is the case, then for a linear function 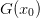 (or
for sufficiently small l),
(or
for sufficiently small l),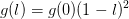
- This should still work well with the relaxes assumptions that:
g is non-negative with an ultimate goal of g=0.
That in the linear regime for small l one has: .. math:
g_l \approx g_0(1 - 2l).
min_step : float
This is the minimum value of l to try before giving up.
min_scale_factor, max_scale_factor : float
l is reduced by a fraction between min_scale_factor and max_scale_factor. The lower scale prevents excessively small steps while the upper scale ensures termination in a reasonable number of steps. If the function is not a minimum and the -2*g0 is a good approximation of the derivative, then arbitrarily small steps will always be accepted. See the Examples below for a demonstration.
max_steps : int
Maximum number of line-search steps to take. Raises NoDescentError if a descent direction has not been found after this many steps.
use_cubic_factor : float
If trust_dg is False, then we use a quadratic interpolation to estimate
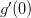 . If the relative error in
this estimate is less than use_cubic_factor, then we use the
cubic interpolation.
. If the relative error in
this estimate is less than use_cubic_factor, then we use the
cubic interpolation.Raises : :class:`NoDescentError` :
If a step cannot be found because function does not decrease fast enough, or step size is too small.
Notes
If the functional form is justified, then we know the slope of
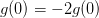 so we can use two points to fit a cubic polynomial
in order to find the optimal
so we can use two points to fit a cubic polynomial
in order to find the optimal 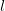 :
: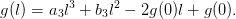
If we only have one point, then we set
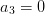 .
.If the functional form is not justified (for example, during a Broyden algorithm where the inverse Jacobian is approximate or incorrect) then this may fail because the slope
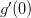 is
incorrect (possibly even with an incorrect sign). In this case,
we fit a quadratic to the previous two points:
is
incorrect (possibly even with an incorrect sign). In this case,
we fit a quadratic to the previous two points: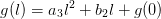
A test is made to see if
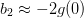 . If so, then the
cubic approximation is used, otherwise the quadratic approximation
is assume (which may allow
. If so, then the
cubic approximation is used, otherwise the quadratic approximation
is assume (which may allow 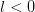 ).
).Examples
Here is a bad problem. The initial step is 500 but a step of about 1 is required, so l is about 1/500 = 0.002.
>>> f = lambda x: x**2 - 1 >>> df = lambda x: 2*x >>> x0 = 0.001 >>> dx = - f(x0)/df(x0) >>> def g(l): ... print l ... return abs(f(x0 + l*dx))**2
>>> l, g_l = line_search(g, g0=g(0), mesgs=_MESGS) 0 1 -0.5 -0.166... -0.076... -0.033... -0.014... -0.006... -0.002... -0.001...
There are quite a few steps here because l must become small. The number of steps can be reduced by reducing the *_scale_factor parameters, but this runs the risk of overshooting and producing extremely small steps. (If the Jacobian is correct, then small enough steps will always be accepted unless at a local minimum).
Note that one can still get hung up at local extrema if not sufficiently close to the solution. In this case, the program should raise an exception.
>>> f = lambda x: (x - 3)*(x*x + 1) >>> df = lambda x: 2*x**2 - 6*x >>> x0 = 1 - 6**(1/2)/3 >>> dx = 0.1 # Correct direction >>> def g(l): ... return abs(f(x0 + l*dx))**2
>>> l, g_l = line_search(g, g0=g(0), mesgs=_MESGS) Traceback (most recent call last): ... NoDescentError: Minimum step-size reached l = ... < 1e-05, err = 2.9... Perhaps a local minimum has been found?