mmf.solve.broyden_solvers

ExtendedBroyden(*varargin, **kwargs)	This solver uses the Extended Broyden algorithm with dynamic restarts toward the specified j_inv0 when the algorithm starts to diverge.
ModifiedBroyden(*varargin, **kwargs)	This solver uses the Modifed Broyden algorithm. >> from solver_interface import Problem, BareState >> class Sqrt(Problem): ... ‘’‘Iterative solution to sqrt(n).’‘’ ... _state_vars = [(‘n’, Required, ‘To compute sqrt(n)’)] ... process_vars() ... def __init__(self, *v, **kw): self.n = np.array(self.n) ... def get_initial_state(self): ... return BareState(x_=copy(self.n)) ... def G(self, x, iter_data, abs_tol, rel_tol, mesgs): ... return x*x - self.n ... ‘Keep x positive’ ... x1 = x ... okay = lambda x: all(x >= 0) ... if not okay(x1): ... x_control = zip(*[(i_, abs(x_)) ... for i_, x_ in enumerate(x1) ... if x_ < 0]) ... x1 = extrapolate(x_controls) ... if not okay(x1): ... x1 = abs(x1) ... G1 = self.G(abs(x), None, abs_tol, rel_tol, mesgs) ... return (x1, G1) >> abs_xtol = 0.01 >> rel_xtol = 0.01 >> solver = ModifiedBroyden(abs_xtol=abs_xtol, rel_xtol=rel_xtol) >> problem = Sqrt(n=[0.01, 1.0, 100.0]) >> state0 = problem.get_initial_state() >> state, niter = solver.solve(problem, state0) >> abs(state.x_[0] - 0.1) < abs_xtol True >> abs(state.x_[1] - 1.0) < abs_xtol True >> abs(state.x_[2] - 10.0) < abs_xtol True >> abs(state.x_[2] - 10.0)/10.0 < rel_xtol True
Broyden(*varargin, **kwargs)	This solver uses the simple Broyden algorithm.
ExtendedBroydenData(*varargin, **kwargs)	Container for Extended Broyden data.
BroydenData(*varargin, **kwargs)	Container for Broyden data.
tst()

Inheritance diagram for mmf.solve.broyden_solvers:

Iterative solvers based on the Broyden method.

This module contains methods for solving root-finding problems with various Broyden algorithms.

The problem is expressed as x = F(x) where the Jacobian of F(x) close to the solution should be close to zero (in other words, the iteration should be as close to convergent as possible) because the Broyden iterations always start with the approximation of an identity J.

Todo

Check usage of max_step. This is now administered in Solver.solve() and should accept a vector.

class mmf.solve.broyden_solvers.ExtendedBroyden(*varargin, **kwargs)

Bases: mmf.solve.broyden_solvers._Broyden

This solver uses the Extended Broyden algorithm with dynamic restarts toward the specified j_inv0 when the algorithm starts to diverge.

ExtendedBroyden(G_tol=1e-12,
                x_tol=1e-12,
                x_tol_rel=1e-12,
                tol_safety_factor=10,
                norm_p=None,
                min_abs_step=1e-12,
                min_rel_step=1e-12,
                max_iter=inf,
                max_time=inf,
                max_step=inf,
                schedule=[],
                verbosity=0,
                message_indent=2,
                mesgs=show=info=False

status=True warn=False error=True iter=False store=info=True status=True warn=True error=True iter=False messages=[],

plot=False, debug=False, n_prev=10, dyadic=False, bad_step_factor=10, weight=0.5, ls_avg_descent_factor=0.0001, ls_min_scale_factor=0.1, ls_max_scale_factor=0.5, ls_linear=True, ls_allow_backstep=True, ls_min_step=1e-12, ls_linear_min_step=None, ls_strategy=default, ls_n_bad_steps=10, ls_allow_bad_steps=False, max_weighted_step=inf, try_weighted_step=True, initial_recession_factor=0.2, recession_factor=0.5, j_inv_incompatibility=0.1, ls_max=10, sensitive_rel_tol=0.1, sensitive_abs_tol=0.01, Jinv_tol=0.01, j_inv0=0.5, n_bad=10, alpha=0.5, x_scale=None, no_restart=False)

Note

In order for this to work reasonably, you must provide a reasonable estimate for x_scale which sets the typical scale over which the function G(x) is linear. If not provided, then IProblem.x_scale will be used.

>>> from solver_interface import Problem, BareState
>>> from mmf.objects import ClassVar
>>> class Sqrt(Problem):
...     '''Iterative solution to sqrt(n).'''
...     _no_name_clash = set(['state0'])
...     _state_vars = [('n', Required, 'To compute sqrt(n)'),
...                    ('state0', Computed)]
...     process_vars()
...     def __init__(self, *v, **kw):
...         self.n = np.array(self.n)
...         self.state0 = self.get_initial_state()
...     def get_initial_state(self):
...         return BareState(x_=copy(self.n))
...     def F(self, x, iter_data=None, abs_tol=None, rel_tol=None,
...           mesgs=[]):
...         return x - (x*x - self.n)
...     def Jinv(self, x):
...         return np.diag(1/(2*x))
...     def step(self, x, x0=None, G0=None, dx0=None, F0=None,
...              compute_G=False, compute_dx=False, compute_F=False,
...              extrapolate=None, iter_data=None,
...              abs_tol=1e-12, rel_tol=1e-12, mesgs=[]):
...         'Keep x positive'
...         x1 = x
...         okay = lambda x: all(x >= 0)
...         if not okay(x1):
...             x_controls = zip(*[(i_, abs(x_))
...                                for i_, x_ in enumerate(x1)
...                                if x_ < 0])
...             x1 = extrapolate(x_controls)
...         if not okay(x1):
...             x1 = abs(x1)
...         F1 = self.F(abs(x), None, abs_tol, rel_tol,  mesgs)
...         G1 = dx1 = None
...         return (x1, G1, dx1, F1)
>>> abs_xtol = 0.01
>>> rel_xtol = 0.01
>>> solver = ExtendedBroyden(x_tol=abs_xtol, x_tol_rel=rel_xtol,
...                          no_restart=True)
>>> problem = Sqrt(n=[0.01, 1.0, 100.0])
>>> state0 = problem.get_initial_state()
>>> state, niter = solver.solve(problem, state0)
>>> abs(state.x_[0] - 0.1) < abs_xtol
True
>>> abs(state.x_[1] - 1.0) < abs_xtol
True
>>> abs(state.x_[2] - 10.0) < abs_xtol
True
>>> abs(state.x_[2] - 10.0)/10.0 < rel_xtol
True

Attributes

State Variables:
G_tol	See ISolver.G_tol
x_tol	See ISolver.x_tol
x_tol_rel	See ISolver.x_tol_rel
tol_safety_factor	“Increase the tolerances when computing function by this amount so that roundoff error will not affect derivative computations etc.
norm_p	See ISolver.norm_p
min_abs_step	Fail if step size falls below this
min_rel_step	Fail if relative step size falls below this
max_iter	Maximum number of iterations.
max_time	Maximum time.
max_step	To prevent too large steps (mainly to prevent converging to an undesired solution) the step size of any component will never be larger than this.
schedule	List of pairs of dictionaries (fn_rep_dict, solver_dict) determining the schedule. The solver the solution will be run through the standard solver with the solver and state updated with these arguments at each stage of the schedule. One might like to start solving with low-resolution and low accuracy, slowly increasing these for example.
verbosity	Level of verbosity: 0 means quiet
message_indent	<no description>
mesgs	Messenger object
plot	If the problem implements IPlotProblem and this is True, then the results are plotted after each iteration.
debug	If True, then store some debugging information in _debug.
dyadic	If True, then use a dyadic representation for Jinv. If this is a number greater than 1, then this number is passed as DyadicSum.n_max limiting the rank of the dyadic representation.
bad_step_factor	If the error increases by more than a factor of bad_step_factor from the previous step, then a weighted step is used. The default is a large value so this does not happen much. If you know that the weighted step will be in the correct direction, then make this smaller. This must be greater than 1 otherwise the method may loop forever.
weight	If the broyden step fails, then the new step is x - w*G(x).
ls_avg_descent_factor	To ensure that we terminate, the line search algorithm requires that each step descend with at least this slope, otherwise the routine will terminate with an error indicating that a local minimum was found rather than a root.
ls_min_scale_factor	Minimum factor by which the step size is reduced in the line search. See solver_utils.line_search().
ls_max_scale_factor	Minimum factor by which the step size is reduced in the line search. See solver_utils.line_search().
ls_linear	If True then the line searches will be along a line. This ensures that bad updates to the inverse Jacobian are completely overwritten, but if the initial direction is not downhill, then this can fail. As a recourse, if the linear search fails, then one pass with the non-linear search is attempted to see if the Jacobian can be compensated. See also ls_linear_min_step. If False, then new directions are used at each step as the inverse Jacobian is updated. Hopefully this will lead to an improved step that is ultimately downhill. Previous bad updates to the inverse Jacobian may not be completely erased.
ls_allow_backstep	If True, then the second line search step (if the first step fails) will be in the negative direction. This may scale the problem inappropriately (especially if a monotonic decrease in a control parameter is desired), in which case one should set this to False.
ls_min_step	To ensure termination, if the relative step size becomes smaller than this, then the routine will terminate with an error.
ls_linear_min_step	If defined, then this will be the bailout criterion for the linear line-search algorithm. This allows for a much earlier bailout from the linear search leaving the high-precision test and ultimate bailout for the subsequent non-linear search. In general, this should be somewhat larger than ls_min_step. If it is not specified, then it is a factor of 100 times larger than ls_min_step.
ls_strategy	Choose the line-search strategy. See iterate() for possibilities.
ls_n_bad_steps	Maximum number of bad steps to try during a line-search phase before giving up.
ls_allow_bad_steps	Set to allow the line search to allow bad steps. Used mainly for debugging, not for production use.
max_weighted_step	Maximum length of the weighted steps (also respects max_step). If this is zero, then weighted steps are never used (except for the first step).
try_weighted_step	If this is True, then a weighed step will be attempted if the other steps fail. This should be True if the iteration is naturally somewhat convergent (i.e. if the objective function has the form G(x) = x - F(x) where the iteration x -> F(x) is somewhat convergent) and should be False if the objective function is unrelated to the steps.
initial_recession_factor	When the error increases by more than bad_step_factor, then the step is regressed toward the previous step by this factor. The regression factor is then further reduced by regression_factor.
recession_factor	When the error increases by more than bad_step_factor, then the step is regressed toward the previous step by this factor until the error is suitably reduced.
j_inv_incompatibility	Maximum incompatibility for an update of the inverse Jacobian to be accepted. See set_point().
ls_max	Maximum number of steps allowed during line search. If the standard iteration fails to improve the solution, then a line search may be used to find the local minimum in the search direction. This can be used to limit or disable this.
sensitive_rel_tol	Sensitive parameters are only adjusted significantly if the relative change in the error of those components is less than this.
sensitive_abs_tol	Sensitive parameters are only adjusted significantly if the absolute change in the error of those components is less than this.
Jinv_tol	This is the tolerance required on the relative change of the predicted step in order to ascertain that the inverse Jacobian is accurate. See _line_search_d().
n_bad	Number of bad steps to allow. When, after this many steps, the best solution has not been improved, then we bail.
x_scale	Typical scale (or vector of scales for each component) over which the function G(x) is approximately linear. This is important for ensuring that the dynamic restart mechanism only restarts components from far away. If None, then IProblem.x_scale will be used.
no_restart	If True then dynamic restarts are not used. Set this if there is no good approximation for j_inv0.
Delegates:
ExtendedBroyden.solver_data0 = ExtendedBroydenData(n_prev=ExtendedBroyden.n_prev=10, j_inv0=ExtendedBroyden.j_inv0=ExtendedBroyden.alpha=0.5)	Blank SolverData instance.
References:
ExtendedBroyden.n_prev -> ExtendedBroyden.solver_data0.n_prev	Number 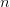of previous steps to keep and use.
ExtendedBroyden.j_inv0 -> ExtendedBroyden.solver_data0.j_inv0	Convergent approximation 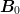to pull back to.
ExtendedBroyden.method -> ExtendedBroyden.solver_data0.j_inv_F.method	‘J’ for Broyden’s good method 1a) and ‘B’ for the “bad” method 2b).
ExtendedBroyden.alpha -> ExtendedBroyden.solver_data0.j_inv0	Linear mixing parameter. If bad steps are taken, then the Jacobian is pulled back to that which will give a linear mixing .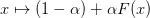
Excluded Variables:
last_state	The last good state. This may be used after an exception is raised to obtain the state that caused the exception or the last good state before the exception occured (in the case of an external interrupt for example. To resume the computation, one should be able to call ISolver.solve() with this state as an input (i.e. this state should be complete with the history set etc. To ensure this, use IState.solver_set_x_()).
_debug	Debugging data.
_f_evals	Total number of function evaluations. Used by solve() and problem_step().
reset_Jinv	If True, then on the next iteration, reset Jinv. Only works once. This can be used in solver_interface.IProblem.schedule to force the Jacobian to be reset.

Methods

all_items()	Return a list [(name, obj)] of (name, object) pairs containing all items available.
archive(name)	Return a string representation that can be executed to restore the object.
archive_1([env])	Return (rep, args, imports).
converged(x, x1, G1, dx1, F1, x0, G0, dx0, ...)	This should return a Converged instance with the
initialize(**kwargs)	Calls __init__() passing all assigned attributes.
items([archive])	Return a list [(name, obj)] of (name, object) pairs where the
iterate(x, problem, solver_data[, x0, G0, ...])	Perform a single iteration and return the triplet
line_search(x, x0, F0, problem, solver_data, ...)	Return (x1, F1) where the step size diminishes sufficiently
line_search_broyden(x, x0, F0, problem, ...)	Return (x1, F1) corresponding to a pure broyden step.
line_search_jacobian(x, x0, F0, problem, ...)	Return (x1, F1).
line_search_linear(x, x0, F0, problem, ...)	Return (x1, F1) where the step size diminishes sufficiently
line_search_non_linear(x, x0, F0, problem, ...)	Return (x1, F1) where the step size diminishes sufficiently
print_iteration_info(iteration_number, ...)	Print iteration information.
problem_F(problem, solver_data, x[, x0, G0, ...])	This should be used instead of calling problem.F() as
problem_G(problem, solver_data, x[, x0, G0, ...])	This should be used instead of calling problem.F() as
problem_step(problem, solver_data, x[, x0, ...])	This should be used instead of calling problem.step() as
resume()	Resume calls to __init__() from __setattr__(),
set_point(j_inv, x, g[, skip_inds, force])	Update the inverse Jacobian if the step is suitable
solve(problem, state[, iterations])	Return the new state representing the solution to the specified problem starting from the specified state.
suspend()	Suspend calls to __init__() from

__init__(*varargin, **kwargs)

iterate(x, problem, solver_data, x0=None, G0=None, dx0=None, F0=None, mesgs=Mesg(show=Container(info=False, status=True, warn=False, error=True, iter=False), store=Container(info=True, status=True, warn=True, error=True, iter=False)))

Perform a single iteration and return the triplet (x_new, (x, G, dx, F)).

The line-search strategy is dictated by ls_strategy which may take on one of the following values.

‘pure_broyden’ : Perform pure Broyden steps irrespective of

whether or not they increase the error. Termination occurs if more than ls_n_bad_step bad steps are taken.

‘1’ :

class mmf.solve.broyden_solvers.ModifiedBroyden(*varargin, **kwargs)

Bases: mmf.solve.broyden_solvers._Broyden

This solver uses the Modifed Broyden algorithm. >> from solver_interface import Problem, BareState >> class Sqrt(Problem): ... ‘’‘Iterative solution to sqrt(n).’‘’ ... _state_vars = [(‘n’, Required, ‘To compute sqrt(n)’)] ... process_vars() ... def __init__(self, *v, **kw): self.n = np.array(self.n) ... def get_initial_state(self): ... return BareState(x_=copy(self.n)) ... def G(self, x, iter_data, abs_tol, rel_tol, mesgs): ... return x*x - self.n ... ‘Keep x positive’ ... x1 = x ... okay = lambda x: all(x >= 0) ... if not okay(x1): ... x_control = zip(*[(i_, abs(x_)) ... for i_, x_ in enumerate(x1) ... if x_ < 0]) ... x1 = extrapolate(x_controls) ... if not okay(x1): ... x1 = abs(x1) ... G1 = self.G(abs(x), None, abs_tol, rel_tol, mesgs) ... return (x1, G1) >> abs_xtol = 0.01 >> rel_xtol = 0.01 >> solver = ModifiedBroyden(abs_xtol=abs_xtol, rel_xtol=rel_xtol) >> problem = Sqrt(n=[0.01, 1.0, 100.0]) >> state0 = problem.get_initial_state() >> state, niter = solver.solve(problem, state0) >> abs(state.x_[0] - 0.1) < abs_xtol True >> abs(state.x_[1] - 1.0) < abs_xtol True >> abs(state.x_[2] - 10.0) < abs_xtol True >> abs(state.x_[2] - 10.0)/10.0 < rel_xtol True

ModifiedBroyden(G_tol=1e-12,
                x_tol=1e-12,
                x_tol_rel=1e-12,
                tol_safety_factor=10,
                norm_p=None,
                min_abs_step=1e-12,
                min_rel_step=1e-12,
                max_iter=inf,
                max_time=inf,
                max_step=inf,
                schedule=[],
                verbosity=0,
                message_indent=2,
                mesgs=show=info=False

status=True warn=False error=True iter=False store=info=True status=True warn=True error=True iter=False messages=[],

plot=False, debug=False, n_prev=10, dyadic=10, bad_step_factor=10, weight=0.5, ls_avg_descent_factor=0.0001, ls_min_scale_factor=0.1, ls_max_scale_factor=0.5, ls_linear=True, ls_allow_backstep=True, ls_min_step=1e-12, ls_linear_min_step=None, ls_strategy=default, ls_n_bad_steps=10, ls_allow_bad_steps=False, max_weighted_step=inf, try_weighted_step=True, initial_recession_factor=0.2, recession_factor=0.5, j_inv_incompatibility=0.1, ls_max=10, sensitive_rel_tol=0.1, sensitive_abs_tol=0.01, Jinv_tol=0.01, alpha=1.0, W=None, DIIS=10, mmf_method=True)

Attributes

State Variables:
G_tol	See ISolver.G_tol
x_tol	See ISolver.x_tol
x_tol_rel	See ISolver.x_tol_rel
tol_safety_factor	“Increase the tolerances when computing function by this amount so that roundoff error will not affect derivative computations etc.
norm_p	See ISolver.norm_p
min_abs_step	Fail if step size falls below this
min_rel_step	Fail if relative step size falls below this
max_iter	Maximum number of iterations.
max_time	Maximum time.
max_step	To prevent too large steps (mainly to prevent converging to an undesired solution) the step size of any component will never be larger than this.
schedule	List of pairs of dictionaries (fn_rep_dict, solver_dict) determining the schedule. The solver the solution will be run through the standard solver with the solver and state updated with these arguments at each stage of the schedule. One might like to start solving with low-resolution and low accuracy, slowly increasing these for example.
verbosity	Level of verbosity: 0 means quiet
message_indent	<no description>
mesgs	Messenger object
plot	If the problem implements IPlotProblem and this is True, then the results are plotted after each iteration.
debug	If True, then store some debugging information in _debug.
bad_step_factor	If the error increases by more than a factor of bad_step_factor from the previous step, then a weighted step is used. The default is a large value so this does not happen much. If you know that the weighted step will be in the correct direction, then make this smaller. This must be greater than 1 otherwise the method may loop forever.
weight	If the broyden step fails, then the new step is x - w*G(x).
ls_avg_descent_factor	To ensure that we terminate, the line search algorithm requires that each step descend with at least this slope, otherwise the routine will terminate with an error indicating that a local minimum was found rather than a root.
ls_min_scale_factor	Minimum factor by which the step size is reduced in the line search. See solver_utils.line_search().
ls_max_scale_factor	Minimum factor by which the step size is reduced in the line search. See solver_utils.line_search().
ls_linear	If True then the line searches will be along a line. This ensures that bad updates to the inverse Jacobian are completely overwritten, but if the initial direction is not downhill, then this can fail. As a recourse, if the linear search fails, then one pass with the non-linear search is attempted to see if the Jacobian can be compensated. See also ls_linear_min_step. If False, then new directions are used at each step as the inverse Jacobian is updated. Hopefully this will lead to an improved step that is ultimately downhill. Previous bad updates to the inverse Jacobian may not be completely erased.
ls_allow_backstep	If True, then the second line search step (if the first step fails) will be in the negative direction. This may scale the problem inappropriately (especially if a monotonic decrease in a control parameter is desired), in which case one should set this to False.
ls_min_step	To ensure termination, if the relative step size becomes smaller than this, then the routine will terminate with an error.
ls_linear_min_step	If defined, then this will be the bailout criterion for the linear line-search algorithm. This allows for a much earlier bailout from the linear search leaving the high-precision test and ultimate bailout for the subsequent non-linear search. In general, this should be somewhat larger than ls_min_step. If it is not specified, then it is a factor of 100 times larger than ls_min_step.
ls_strategy	Choose the line-search strategy. See iterate() for possibilities.
ls_n_bad_steps	Maximum number of bad steps to try during a line-search phase before giving up.
ls_allow_bad_steps	Set to allow the line search to allow bad steps. Used mainly for debugging, not for production use.
max_weighted_step	Maximum length of the weighted steps (also respects max_step). If this is zero, then weighted steps are never used (except for the first step).
try_weighted_step	If this is True, then a weighed step will be attempted if the other steps fail. This should be True if the iteration is naturally somewhat convergent (i.e. if the objective function has the form G(x) = x - F(x) where the iteration x -> F(x) is somewhat convergent) and should be False if the objective function is unrelated to the steps.
initial_recession_factor	When the error increases by more than bad_step_factor, then the step is regressed toward the previous step by this factor. The regression factor is then further reduced by regression_factor.
recession_factor	When the error increases by more than bad_step_factor, then the step is regressed toward the previous step by this factor until the error is suitably reduced.
j_inv_incompatibility	Maximum incompatibility for an update of the inverse Jacobian to be accepted. See set_point().
ls_max	Maximum number of steps allowed during line search. If the standard iteration fails to improve the solution, then a line search may be used to find the local minimum in the search direction. This can be used to limit or disable this.
sensitive_rel_tol	Sensitive parameters are only adjusted significantly if the relative change in the error of those components is less than this.
sensitive_abs_tol	Sensitive parameters are only adjusted significantly if the absolute change in the error of those components is less than this.
Jinv_tol	This is the tolerance required on the relative change of the predicted step in order to ascertain that the inverse Jacobian is accurate. See _line_search_d().
alpha	<no description>
W	<no description>
DIIS	Size of DIIS subspace
mmf_method	Use my DIIS method rather than the usual.
Delegates:
ModifiedBroyden.solver_data0 = BroydenData(dyadic=ModifiedBroyden.dyadic=10, n_prev=ModifiedBroyden.n_prev=10)	Blank SolverData instance.
References:
ModifiedBroyden.n_prev -> ModifiedBroyden.solver_data0.n_prev	Number of previous steps to store.
ModifiedBroyden.dyadic -> ModifiedBroyden.solver_data0.dyadic	If True, then use a dyadic representation for Jinv. If this is a number greater than 1, then this number is passed as DyadicSum.n_max limiting the rank of the dyadic representation.
Excluded Variables:
last_state	The last good state. This may be used after an exception is raised to obtain the state that caused the exception or the last good state before the exception occured (in the case of an external interrupt for example. To resume the computation, one should be able to call ISolver.solve() with this state as an input (i.e. this state should be complete with the history set etc. To ensure this, use IState.solver_set_x_()).
_debug	Debugging data.
_f_evals	Total number of function evaluations. Used by solve() and problem_step().
reset_Jinv	If True, then on the next iteration, reset Jinv. Only works once. This can be used in solver_interface.IProblem.schedule to force the Jacobian to be reset.

Methods

all_items()	Return a list [(name, obj)] of (name, object) pairs containing all items available.
archive(name)	Return a string representation that can be executed to restore the object.
archive_1([env])	Return (rep, args, imports).
converged(x, x1, G1, dx1, F1, x0, G0, dx0, ...)	This should return a Converged instance with the
initialize(**kwargs)	Calls __init__() passing all assigned attributes.
items([archive])	Return a list [(name, obj)] of (name, object) pairs where the
iterate(x, problem, solver_data[, x0, G0, ...])	Perform a single iteration and return the triplet
line_search(x, x0, F0, problem, solver_data, ...)	Return (x1, F1) where the step size diminishes sufficiently
line_search_broyden(x, x0, F0, problem, ...)	Return (x1, F1) corresponding to a pure broyden step.
line_search_jacobian(x, x0, F0, problem, ...)	Return (x1, F1).
line_search_linear(x, x0, F0, problem, ...)	Return (x1, F1) where the step size diminishes sufficiently
line_search_non_linear(x, x0, F0, problem, ...)	Return (x1, F1) where the step size diminishes sufficiently
print_iteration_info(iteration_number, ...)	Print iteration information.
problem_F(problem, solver_data, x[, x0, G0, ...])	This should be used instead of calling problem.F() as
problem_G(problem, solver_data, x[, x0, G0, ...])	This should be used instead of calling problem.F() as
problem_step(problem, solver_data, x[, x0, ...])	This should be used instead of calling problem.step() as
resume()	Resume calls to __init__() from __setattr__(),
set_point(j_inv, x, g[, skip_inds, force])	Update the inverse Jacobian if the step is suitable
solve(problem, state[, iterations])	Return the new state representing the solution to the specified problem starting from the specified state.
suspend()	Suspend calls to __init__() from

__init__(*varargin, **kwargs)

class mmf.solve.broyden_solvers.Broyden(*varargin, **kwargs)

Bases: mmf.solve.broyden_solvers._Broyden

This solver uses the simple Broyden algorithm.

Examples

>>> from solver_interface import Problem, BareState
>>> class Sqrt(Problem):
...     '''Iterative solution to sqrt(n).'''
...     _state_vars = [('n', Required, 'To compute sqrt(n)'),
...                    ('state0', Computed)]
...     process_vars()
...     def __init__(self, *v, **kw):
...         self.n = np.array(self.n)
...         self.state0 = self.get_initial_state()
...     def get_initial_state(self):
...         return BareState(x_=copy(self.n))
...     def F(self, x, iter_data=None, abs_tol=None, rel_tol=None,
...           mesgs=_MESGS):
...         return x - (x*x - self.n)
...     def Jinv(self, x):
...         return np.diag(1/(2*x))
...     def step(self, x, x0=None, G0=None, dx0=None, F0=None,
...              compute_G=False, compute_dx=False, compute_F=False,
...              extrapolate=None, iter_data=None,
...              abs_tol=1e-12, rel_tol=1e-12, mesgs=_MESGS):
...         'Keep x positive'
...         x1 = x
...         okay = lambda x: all(x >= 0)
...         if not okay(x1):
...             x_controls = zip(*[(i_, abs(x_))
...                                for i_, x_ in enumerate(x1)
...                                if x_ < 0])
...             x1 = extrapolate(x_controls)
...         if not okay(x1):
...             x1 = abs(x1)
...         F1 = self.F(abs(x), None, abs_tol, rel_tol,  mesgs)
...         G1 = dx1 = None
...         return (x1, G1, dx1, F1)
>>> x_tol = 0.01
>>> G_tol = 0.01
>>> solver = Broyden(x_tol=x_tol, G_tol=G_tol, ls_max=100,
...                  ls_strategy='default', dyadic=2, n_prev=2)
>>> problem = Sqrt(n=[0.01, 1.0, 100.0])
>>> state0 = problem.get_initial_state()
>>> state, niter = solver.solve(problem, state0)
>>> niter              # Newton takes 5, straight Broyden takes 21
10
>>> abs(state.x_[0] - 0.1) < 1.2*x_tol
True
>>> abs(state.x_[1] - 1.0) < 1.2*x_tol
True
>>> abs(state.x_[2] - 10.0) < x_tol
True
>>> G, dx = problem.G(state.x_)
>>> abs(G).max() < G_tol
True

Methods

all_items()	Return a list [(name, obj)] of (name, object) pairs containing all items available.
archive(name)	Return a string representation that can be executed to restore the object.
archive_1([env])	Return (rep, args, imports).
converged(x, x1, G1, dx1, F1, x0, G0, dx0, ...)	This should return a Converged instance with the
initialize(**kwargs)	Calls __init__() passing all assigned attributes.
items([archive])	Return a list [(name, obj)] of (name, object) pairs where the
iterate(x, problem, solver_data[, x0, G0, ...])	Perform a single iteration and return the triplet
line_search(x, x0, F0, problem, solver_data, ...)	Return (x1, F1) where the step size diminishes sufficiently
line_search_broyden(x, x0, F0, problem, ...)	Return (x1, F1) corresponding to a pure broyden step.
line_search_jacobian(x, x0, F0, problem, ...)	Return (x1, F1).
line_search_linear(x, x0, F0, problem, ...)	Return (x1, F1) where the step size diminishes sufficiently
line_search_non_linear(x, x0, F0, problem, ...)	Return (x1, F1) where the step size diminishes sufficiently
print_iteration_info(iteration_number, ...)	Print iteration information.
problem_F(problem, solver_data, x[, x0, G0, ...])	This should be used instead of calling problem.F() as
problem_G(problem, solver_data, x[, x0, G0, ...])	This should be used instead of calling problem.F() as
problem_step(problem, solver_data, x[, x0, ...])	This should be used instead of calling problem.step() as
resume()	Resume calls to __init__() from __setattr__(),
set_point(j_inv, x, g[, skip_inds, force])	Update the inverse Jacobian if the step is suitable
solve(problem, state[, iterations])	Return the new state representing the solution to the specified problem starting from the specified state.
suspend()	Suspend calls to __init__() from

__init__(*varargin, **kwargs)

class mmf.solve.broyden_solvers.ExtendedBroydenData(*varargin, **kwargs)

Bases: mmf.solve.broyden_solvers.BroydenData

Container for Extended Broyden data.

ExtendedBroydenData(iter_data=None,
                    iteration_number=0,
                    j_inv_G=,
                    dyadic=False,
                    x0=None,
                    g0=None,
                    skip_0=None,
                    x_good_0=None,
                    g_good_0=None,
                    x_good_1=None,
                    g_good_1=None,
                    skip_good=None,
                    old_err=inf,
                    inv_jacobian_err=inf)

The core for this method is defined in mmf.solve.JinvExtendedBroydenFull and a proxy object is used to maintain the state and compute the updates.

Attributes

class mmf.solve.broyden_solvers.BroydenData(*varargin, **kwargs)

Bases: mmf.solve.solver_interface.SolverData

Container for Broyden data.

BroydenData(iter_data=None,
            iteration_number=0,
            j_inv_G=,
            dyadic=True,
            x0=None,
            g0=None,
            skip_0=None,
            x_good_0=None,
            g_good_0=None,
            x_good_1=None,
            g_good_1=None,
            skip_good=None,
            old_err=inf,
            inv_jacobian_err=inf)

The core for this method is defined in mmf.solve.JinvBroyden and a proxy object is used to maintain the state and compute the updates.

Attributes

mmf.solve.broyden_solvers.tst()