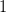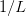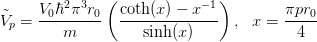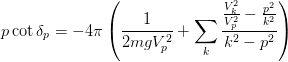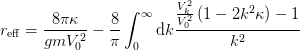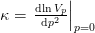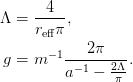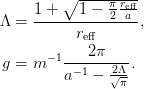mmf.physics.potentials.separable¶
| VPoschlTeller(*varargin, **kwargs) | Poschl-Teller potential used by GFMC groups. |
| Separable(*varargin, **kwargs) | Base class for separable potentials, including methods to compute their scattering properties: 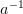 and and 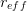 are computed by potentials.ainv() and potentials.reff(). are computed by potentials.ainv() and potentials.reff(). |
| SharpCutoff(*varargin, **kwargs) | Separable potential with a sharp momentum cutoff. |
| SmoothCutoff(*varargin, **kwargs) | Separable potential with a smooth momentum cutoff. |
| Yamaguchi(*varargin, **kwargs) | Separable Yamaguchi potential. |
| EffectiveRange(*varargin, **kwargs) | Separable Effective Range Interaction, completely determined by the scattering length and effective range. |
Inheritance diagram for mmf.physics.potentials.separable:
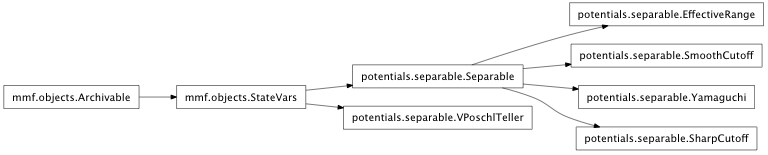
Separable Potentials.
This module contains various three-dimensional separable potentials of the form
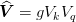
The relevant one-body Schrodinger equation becomes in momentum space (for bound states):
The effective range expansion can be expressed succinctly for separable potentials:
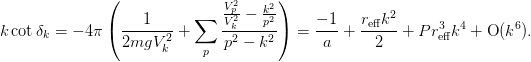
The first two coefficients are computed by the methods Separable.ainv() and Separable.reff().
Note
Everything here is expressed in units where
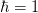 . To restore these constants make the following
substitutions. Also, these units are for the one-body problem: i.e.
. To restore these constants make the following
substitutions. Also, these units are for the one-body problem: i.e.  is
the mass of a single species. If you wish to use these for the two-body
problem, be sure to use the reduced mass in place of
is
the mass of a single species. If you wish to use these for the two-body
problem, be sure to use the reduced mass in place of  .
.
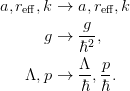
The dimensions are thus:
- [
] :
which implies
.
- [
] :
- [
] :
.
- [
] = [
] :
- class mmf.physics.potentials.separable.VPoschlTeller(*varargin, **kwargs)[source]¶
Bases: mmf.objects.StateVars
Poschl-Teller potential used by GFMC groups.
VPoschlTeller(V0=-1.0, r0=Required)
Attributes
State Variables: - V0¶
Strength of the potential. - r0¶
Range of potential. (This is only the effective range if V0 = -1) Methods
V(r[, m]) Vp(p[, m]) Fourier transform of potential. Vpq(p, q[, m]) Integrated potential over angles that appears in the BCS all_items() Return a list [(name, obj)] of (name, object) pairs containing all items available. archive(name) Return a string representation that can be executed to restore the object. archive_1([env]) Return (rep, args, imports). initialize(**kwargs) Calls __init__() passing all assigned attributes. items([archive]) Return a list [(name, obj)] of (name, object) pairs where the resume() Resume calls to __init__() from __setattr__(), suspend() Suspend calls to __init__() from This is the initialization routine. It is called after the attributes specified in _state_vars have been assigned.
The user version should perform any after-assignment initializations that need to be performed.
Note
Since all of the initial arguments are listed in kwargs, this can be used as a list of attributes that have “changed” allowing the initialization to be streamlined. The default __setattr__() method will call __init__() with the changed attribute to allow for recalculation.
This recomputing only works for attributes that are assigned, i.e. iff __setattr__() is called. If an attribute is mutated, then __getattr__() is called and there is no (efficient) way to determine if it was mutated.
Computed values with True Computed.save will be passed in through kwargs when objects are restored from an archive. These parameters in general need not be recomputed, but this opens the possibility for an inconsistent state upon construction if a user inadvertently provides these parameters. Note that the parameters still cannot be set directly.
See __init__() Semantics for details.
Methods
V(r[, m]) Vp(p[, m]) Fourier transform of potential. Vpq(p, q[, m]) Integrated potential over angles that appears in the BCS all_items() Return a list [(name, obj)] of (name, object) pairs containing all items available. archive(name) Return a string representation that can be executed to restore the object. archive_1([env]) Return (rep, args, imports). initialize(**kwargs) Calls __init__() passing all assigned attributes. items([archive]) Return a list [(name, obj)] of (name, object) pairs where the resume() Resume calls to __init__() from __setattr__(), suspend() Suspend calls to __init__() from - __init__(*varargin, **kwargs)¶
This is the initialization routine. It is called after the attributes specified in _state_vars have been assigned.
The user version should perform any after-assignment initializations that need to be performed.
Note
Since all of the initial arguments are listed in kwargs, this can be used as a list of attributes that have “changed” allowing the initialization to be streamlined. The default __setattr__() method will call __init__() with the changed attribute to allow for recalculation.
This recomputing only works for attributes that are assigned, i.e. iff __setattr__() is called. If an attribute is mutated, then __getattr__() is called and there is no (efficient) way to determine if it was mutated.
Computed values with True Computed.save will be passed in through kwargs when objects are restored from an archive. These parameters in general need not be recomputed, but this opens the possibility for an inconsistent state upon construction if a user inadvertently provides these parameters. Note that the parameters still cannot be set directly.
See __init__() Semantics for details.
- Vpq(p, q, m=1.0)[source]¶
Integrated potential over angles that appears in the BCS s-wave gap equation:
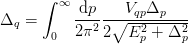
Notes
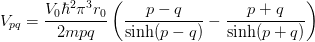
Examples
>>> V = VPoschlTeller(r0=1) >>> p = np.array([[0,1,2]]) >>> q = p.T >>> V.Vpq(p,q) array([[-6.57973627, -6.21059264, -5.25788171], [-6.21059264, -5.88551639, -5.03455853], [-5.25788171, -5.03455853, -4.4270986 ]])
- class mmf.physics.potentials.separable.Separable(*varargin, **kwargs)[source]¶
Bases: mmf.objects.StateVars
Base class for separable potentials, including methods to compute their scattering properties:
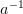 and
and 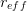 are computed by potentials.ainv() and potentials.reff().
are computed by potentials.ainv() and potentials.reff().Separable(g=-1.0, m=1.0)
Notes
These potentials have the form:
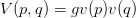
Our convention for normalization is that v(0) = 1. By default, the coupling constant is set to -1, so the potential is attractive. The form-factors
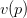 should be functions
that decay for large momenta and are roughly constant for small
momenta.
should be functions
that decay for large momenta and are roughly constant for small
momenta.Attributes
State Variables: - g¶
Coupling constant - m¶
Mass. Set to reduced mass for two-body Computed Variables: - inf¶
Infinite endpoint wrapped with a Decay subclass to encode the nature of the decay. List of typical/critical momenta. The points should be carefully inspected during integration etc. Methods
ainv([abs_tol, rel_tol]) Return the inverse s-wave scattering-length. all_items() Return a list [(name, obj)] of (name, object) pairs containing all items available. archive(name) Return a string representation that can be executed to restore the object. archive_1([env]) Return (rep, args, imports). initialize(**kwargs) Calls __init__() passing all assigned attributes. items([archive]) Return a list [(name, obj)] of (name, object) pairs where the k_cot_delta(p2[, abs_tol, rel_tol]) Return the phase shift 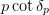 as a function of
as a function of 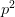 .
.reff([abs_tol, rel_tol]) Return the s-wave effective range. resume() Resume calls to __init__() from __setattr__(), set_g(ainv[, reff]) Set the coupling and Lambda to fix the scattering length suspend() Suspend calls to __init__() from v(p) Return the form factor. Subclasses should call to add p_c to self.V
Methods
ainv([abs_tol, rel_tol]) Return the inverse s-wave scattering-length. all_items() Return a list [(name, obj)] of (name, object) pairs containing all items available. archive(name) Return a string representation that can be executed to restore the object. archive_1([env]) Return (rep, args, imports). initialize(**kwargs) Calls __init__() passing all assigned attributes. items([archive]) Return a list [(name, obj)] of (name, object) pairs where the k_cot_delta(p2[, abs_tol, rel_tol]) Return the phase shift 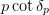 as a function of
as a function of 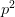 .
.reff([abs_tol, rel_tol]) Return the s-wave effective range. resume() Resume calls to __init__() from __setattr__(), set_g(ainv[, reff]) Set the coupling and Lambda to fix the scattering length suspend() Suspend calls to __init__() from v(p) Return the form factor. - ainv(abs_tol=1e-12, rel_tol=1e-12)[source]¶
Return the inverse s-wave scattering-length.
Notes
This is computed by
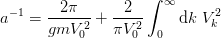
- p_c[source]
List of typical/critical momenta. The points should be carefully inspected during integration etc.
- class mmf.physics.potentials.separable.SharpCutoff(*varargin, **kwargs)[source]¶
Bases: mmf.physics.potentials.separable.Separable
Separable potential with a sharp momentum cutoff.
SharpCutoff(g=-1.0, m=1.0, Lambda=1.0)
Notes
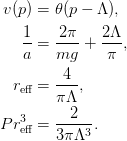
assume(L>0);assume(k>0);assume(p>0);additionally(L>k): kcd:=(v)->-4*Pi*(1/2/m/g/v(k)**2 + int((v(p)**2/v(k)**2 - k^2/p^2)/(p^2-k^2)*p^2/2/Pi^2,p=0..infinity)): v:=p->Heaviside(L-p): ainv=-subs(k=0,kcd(v)); re=2*coeff(series(kcd(v),k,6),k,2); P*re^3=coeff(series(kcd(v),k,6),k,4);Examples
>>> V = SharpCutoff(Lambda=10.0) >>> V.set_g(ainv=1.0, reff=0.1) >>> V.ainv() 1.00000000... >>> V.reff() 0.10000000...
Attributes
State Variables: - g¶
Coupling constant - m¶
Mass. Set to reduced mass for two-body - Lambda¶
Momentum cutoff Computed Variables: - inf¶
Infinite endpoint wrapped with a Decay subclass to encode the nature of the decay. - p_c¶
List of typical/critical momenta. The points should be carefully inspected during integration etc. Methods
ainv([abs_tol, rel_tol]) Return the inverse s-wave scattering-length. all_items() Return a list [(name, obj)] of (name, object) pairs containing all items available. archive(name) Return a string representation that can be executed to restore the object. archive_1([env]) Return (rep, args, imports). initialize(**kwargs) Calls __init__() passing all assigned attributes. items([archive]) Return a list [(name, obj)] of (name, object) pairs where the k_cot_delta(p2[, abs_tol, rel_tol]) Return the phase shift 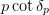 as a function of
as a function of 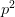 .
.reff([abs_tol, rel_tol]) Return the s-wave effective range. resume() Resume calls to __init__() from __setattr__(), set_g(ainv[, reff]) Set the coupling to fix the scattering length. suspend() Suspend calls to __init__() from v(p) Subclasses should call to add p_c to self.V
Methods
ainv([abs_tol, rel_tol]) Return the inverse s-wave scattering-length. all_items() Return a list [(name, obj)] of (name, object) pairs containing all items available. archive(name) Return a string representation that can be executed to restore the object. archive_1([env]) Return (rep, args, imports). initialize(**kwargs) Calls __init__() passing all assigned attributes. items([archive]) Return a list [(name, obj)] of (name, object) pairs where the k_cot_delta(p2[, abs_tol, rel_tol]) Return the phase shift 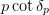 as a function of
as a function of 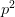 .
.reff([abs_tol, rel_tol]) Return the s-wave effective range. resume() Resume calls to __init__() from __setattr__(), set_g(ainv[, reff]) Set the coupling to fix the scattering length. suspend() Suspend calls to __init__() from v(p) - __init__(*varargin, **kwargs)¶
Subclasses should call to add p_c to self.V
- class mmf.physics.potentials.separable.SmoothCutoff(*varargin, **kwargs)[source]¶
Bases: mmf.physics.potentials.separable.Separable
Separable potential with a smooth momentum cutoff.
SmoothCutoff(g=-1.0, m=1.0, Lambda=1.0)
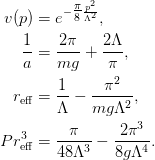
assume(L>0);assume(k>0);assume(p>0);additionally(L>k): kcd:=(v)->-4*Pi*(1/2/m/g/v(k)**2 + int((v(p)**2/v(k)**2 - k^2/p^2)/(p^2-k^2)*p^2/2/Pi^2,p=0..infinity)): v:=p->exp(-Pi/8*p^2/L^2): eqs:={ainv=-expand(simplify(eval(subs(k=0,kcd(v))))), re=2*expand(simplify(coeff(series(kcd(v),k,6),k,2)))}; P*re^3=coeff(series(kcd(v),k,6),k,4); solve(eqs,[g,L]);Examples
>>> a = 1.0 >>> V = SmoothCutoff(Lambda=10.0) >>> V.set_g(ainv=1.0, reff=0.1) >>> V.ainv() 1.000000000... >>> V.reff() 0.100000000...
Attributes
State Variables: - g¶
Coupling constant - m¶
Mass. Set to reduced mass for two-body - Lambda¶
Momentum cutoff Computed Variables: - inf¶
Infinite endpoint wrapped with a Decay subclass to encode the nature of the decay. - p_c¶
List of typical/critical momenta. The points should be carefully inspected during integration etc. Methods
ainv([abs_tol, rel_tol]) Return the inverse s-wave scattering-length. all_items() Return a list [(name, obj)] of (name, object) pairs containing all items available. archive(name) Return a string representation that can be executed to restore the object. archive_1([env]) Return (rep, args, imports). initialize(**kwargs) Calls __init__() passing all assigned attributes. items([archive]) Return a list [(name, obj)] of (name, object) pairs where the k_cot_delta(p2[, abs_tol, rel_tol]) Return the phase shift 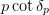 as a function of
as a function of 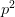 .
.reff([abs_tol, rel_tol]) Return the s-wave effective range. resume() Resume calls to __init__() from __setattr__(), set_g(ainv[, reff]) Set the coupling to fix the scattering length. suspend() Suspend calls to __init__() from v(p) Subclasses should call to add p_c to self.V
Methods
ainv([abs_tol, rel_tol]) Return the inverse s-wave scattering-length. all_items() Return a list [(name, obj)] of (name, object) pairs containing all items available. archive(name) Return a string representation that can be executed to restore the object. archive_1([env]) Return (rep, args, imports). initialize(**kwargs) Calls __init__() passing all assigned attributes. items([archive]) Return a list [(name, obj)] of (name, object) pairs where the k_cot_delta(p2[, abs_tol, rel_tol]) Return the phase shift 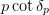 as a function of
as a function of 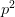 .
.reff([abs_tol, rel_tol]) Return the s-wave effective range. resume() Resume calls to __init__() from __setattr__(), set_g(ainv[, reff]) Set the coupling to fix the scattering length. suspend() Suspend calls to __init__() from v(p) - __init__(*varargin, **kwargs)¶
Subclasses should call to add p_c to self.V
- class mmf.physics.potentials.separable.Yamaguchi(*varargin, **kwargs)[source]¶
Bases: mmf.physics.potentials.separable.Separable
Separable Yamaguchi potential.
Yamaguchi(g=-1.0, m=1.0, Lambda=1.0)
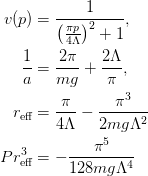
assume(L>0);assume(k>0);assume(p>0);additionally(L>k): kcd:=(v)->-4*Pi*(1/2/m/g/v(k)**2 + int((v(p)**2/v(k)**2 - k^2/p^2)/(p^2-k^2)*p^2/2/Pi^2,p=0..infinity)): v:=p->1/(1+(Pi*p/4/L)^2): eqs:={ainv=-expand(simplify(eval(subs(k=0,kcd(v))))), re=2*expand(simplify(coeff(series(kcd(v),k,6),k,2)))}; P*re^3=coeff(series(kcd(v),k,6),k,4); solve(eqs,[g,L]); simplify(expand(rationalize(allvalues(solve(eqs,[g,L]))[1][1])));Note: this has a closed effective range expansion with three terms.
Examples
>>> V = Yamaguchi(Lambda=10.0) >>> V.set_g(ainv=1.0,reff=0.5) >>> V.ainv() 1.0... >>> V.reff() 0.499999...
Attributes
State Variables: - g¶
Coupling constant - m¶
Mass. Set to reduced mass for two-body - Lambda¶
Momentum cutoff Computed Variables: - inf¶
Infinite endpoint wrapped with a Decay subclass to encode the nature of the decay. - p_c¶
List of typical/critical momenta. The points should be carefully inspected during integration etc. Methods
ainv([abs_tol, rel_tol]) Return the inverse s-wave scattering-length. all_items() Return a list [(name, obj)] of (name, object) pairs containing all items available. archive(name) Return a string representation that can be executed to restore the object. archive_1([env]) Return (rep, args, imports). initialize(**kwargs) Calls __init__() passing all assigned attributes. items([archive]) Return a list [(name, obj)] of (name, object) pairs where the k_cot_delta(p2[, abs_tol, rel_tol]) Return the phase shift 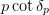 as a function of
as a function of 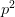 .
.reff([abs_tol, rel_tol]) Return the s-wave effective range. resume() Resume calls to __init__() from __setattr__(), set_g(ainv[, reff]) Set the coupling and Lambda to fix the scattering length suspend() Suspend calls to __init__() from v(p) Subclasses should call to add p_c to self.V
Methods
ainv([abs_tol, rel_tol]) Return the inverse s-wave scattering-length. all_items() Return a list [(name, obj)] of (name, object) pairs containing all items available. archive(name) Return a string representation that can be executed to restore the object. archive_1([env]) Return (rep, args, imports). initialize(**kwargs) Calls __init__() passing all assigned attributes. items([archive]) Return a list [(name, obj)] of (name, object) pairs where the k_cot_delta(p2[, abs_tol, rel_tol]) Return the phase shift 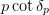 as a function of
as a function of 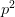 .
.reff([abs_tol, rel_tol]) Return the s-wave effective range. resume() Resume calls to __init__() from __setattr__(), set_g(ainv[, reff]) Set the coupling and Lambda to fix the scattering length suspend() Suspend calls to __init__() from v(p) - __init__(*varargin, **kwargs)¶
Subclasses should call to add p_c to self.V
- class mmf.physics.potentials.separable.EffectiveRange(*varargin, **kwargs)[source]¶
Bases: mmf.physics.potentials.separable.Separable
Separable Effective Range Interaction, completely determined by the scattering length and effective range.
EffectiveRange(g=-1.0, m=1.0, Lambda=1.0)
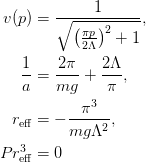
assume(L>0);assume(k>0);assume(p>0);additionally(L>k): kcd:=(v)->-4*Pi*(1/2/m/g/v(k)**2 + int((v(p)**2/v(k)**2 - k^2/p^2)/(p^2-k^2)*p^2/2/Pi^2,p=0..infinity)): v:=p->1/sqrt((Pi*p/2/L)^2+1): eqs:={ainv=-expand(simplify(eval(subs(k=0,kcd(v))))), re=2*expand(simplify(coeff(series(kcd(v),k,6),k,2)))}; P*re^3=coeff(series(kcd(v),k,6),k,4); simplify(expand(rationalize(subs(allvalues(solve(eqs,[g,L]))[1][1],L)),symbolic)); solve(eqs,[g,L]);Note that this as a closed effective range expansion stopping at the second term.
Examples
>>> V = EffectiveRange(Lambda=10.0) >>> V.set_g(ainv=1.0,reff=0.5) >>> V.ainv() 1.000000... >>> V.reff() 0.500000...
Attributes
State Variables: - g¶
Coupling constant - m¶
Mass. Set to reduced mass for two-body - Lambda¶
Momentum cutoff Computed Variables: - inf¶
Infinite endpoint wrapped with a Decay subclass to encode the nature of the decay. - p_c¶
List of typical/critical momenta. The points should be carefully inspected during integration etc. Methods
ainv([abs_tol, rel_tol]) Return the inverse s-wave scattering-length. all_items() Return a list [(name, obj)] of (name, object) pairs containing all items available. archive(name) Return a string representation that can be executed to restore the object. archive_1([env]) Return (rep, args, imports). initialize(**kwargs) Calls __init__() passing all assigned attributes. items([archive]) Return a list [(name, obj)] of (name, object) pairs where the k_cot_delta(p2[, abs_tol, rel_tol]) Return the phase shift 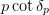 as a function of
as a function of 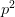 .
.reff([abs_tol, rel_tol]) Return the s-wave effective range. resume() Resume calls to __init__() from __setattr__(), set_g(ainv[, reff]) Set the coupling and Lambda to fix the scattering length suspend() Suspend calls to __init__() from v(p) Subclasses should call to add p_c to self.V
Methods
ainv([abs_tol, rel_tol]) Return the inverse s-wave scattering-length. all_items() Return a list [(name, obj)] of (name, object) pairs containing all items available. archive(name) Return a string representation that can be executed to restore the object. archive_1([env]) Return (rep, args, imports). initialize(**kwargs) Calls __init__() passing all assigned attributes. items([archive]) Return a list [(name, obj)] of (name, object) pairs where the k_cot_delta(p2[, abs_tol, rel_tol]) Return the phase shift 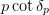 as a function of
as a function of 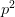 .
.reff([abs_tol, rel_tol]) Return the s-wave effective range. resume() Resume calls to __init__() from __setattr__(), set_g(ainv[, reff]) Set the coupling and Lambda to fix the scattering length suspend() Suspend calls to __init__() from v(p) - __init__(*varargin, **kwargs)¶
Subclasses should call to add p_c to self.V