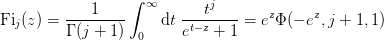Navigation

Previous topic

mmf.math.special.fermi

Next topic

mmf.objects

This Page

mmf.math.special.lerch

LerchPhi(z, s, a) Return the Lerch Trancident function 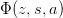\Phi(z,s,a) on a restricted
Li(s, z) Return the polylogarithm 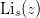\Li_s(z).
Fi(j, z) Return the complete Fermi-Dirac integral 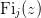\operatorname{Fi}_{j}(z).

Module of routines for computing the Lerch Trancendent and related functions.

We have the Lerch Trancendent 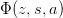\Phi(z,s,a), the Polylogarithm \Li_s(z):

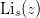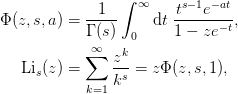
\begin{aligned} \Phi(z,s,a) &= \frac{1}{\Gamma(s)}\int_0^\infty \d{t}\; \frac{t^{s-1}e^{-at}}{1-ze^{-t}},\\ \Li_s(z) &= \sum_{k=1}^{\infty} \frac{z^{k}}{k^s} = z\Phi(z, s, 1), \end{aligned}

The Fermi-Dirac integrals can be expressed in terms of these:

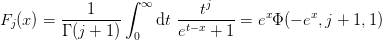
\begin{aligned} F_{j}(x) &= \frac{1}{\Gamma(j + 1)}\int_{0}^{\infty}\d{t}\; \frac{t^{j}}{e^{t - x} + 1} = e^{x}\Phi(-e^{x},j+1,1) \end{aligned}

mmf.math.special.lerch.LerchPhi(z, s, a)[source]

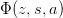Return the Lerch Trancident function \Phi(z,s,a) on a restricted domain.

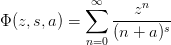
\Phi(z,s,a) = \sum_{n=0}^\infty \frac{z^n}{(n+a)^s}

Computes the result using the integral representation

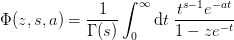
\Phi(z,s,a) = \frac{1}{\Gamma(s)}\int_0^\infty \d{t}\; \frac{t^{s-1}e^{-at}}{1-ze^{-t}}

Examples

>>> abs(LerchPhi(1,2,3) - (np.pi**2/6.0 - 5.0/4.0)) < 1e-12
True
>>> abs(LerchPhi(0.5,2,3) - 0.157924211720100047221250) < 1e-12
True
mmf.math.special.lerch.Li(s, z)[source]

Return the polylogarithm \Li_s(z).

\Li_s(z) &= \sum_{k=1}^{\infty} \frac{z^k}{k^s} = z\Phi(z, s, 1),

mmf.math.special.lerch.Fi(j, z)[source]

Return the complete Fermi-Dirac integral \operatorname{Fi}_{j}(z).

\operatorname{Fi}_{j}(z) &= \frac{1}{\Gamma(j + 1)}\int_{0}^{\infty}\d{t}\; \frac{t^{j}}{e^{t - z} + 1} = e^{z}\Phi(-e^{z},j+1,1)

Navigation

© Copyright 2010, Michael McNeil Forbes. Last updated on 17 September 2012. Created using Sphinx 1.1.3.