mmf.math.ode.test_deq

Consider a first-order ODE:

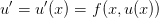
and a transformation to a new set of variables 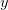, 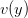defined by

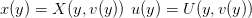
Taking the differentials we obtain a set of linear equations:

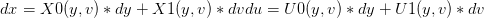
from which we can isolate

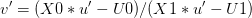
which may be fully expressed in terms of 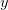and via the relations.

For a system of first-order equations (and any system can be reduced to this) we have

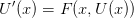
and a transformation to a new set of variables 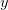, 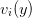defined by

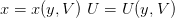
Taking the differentials we obtain a set of linear equations:

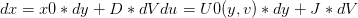
from which we may isolate

We obtain the transformed equations:

from sympy import *

m = 2 for _i in xrange(m+1):

var(‘u%i’ % _i) var(‘v%i’ % _i)

x, y, f = var([‘x’,’y’,’f’]) X, U = var([‘X’,’U’]) X1, U1 = var([‘X1’,’U1’]) X2, U2 = var([‘X2’,’U2’])

eq1 = u(x).diff(x,x) - f(x, u(x), u(x).diff(x)) trans = {x: X(y(x), v(y(x))), u(x): U(y(x), v(y(x)))}

sy = {y:y(x), v:v(y(x))} sx = {u:u(x)} simp = {

u(x).diff(x):u1, u(x).diff(x,x):u2, v(y).diff(y).subs(sy):v1, v(y).diff(y,y).subs(sy):v2, X(y,v).diff(y).subs(sy):X1, X(y,v).diff(v).subs(sy):X2, U(y,v).diff(y).subs(sy):U1, U(y,v).diff(v).subs(sy):U2}

{y(x).diff(x):solve(trans[x].diff(x) - 1, y(x).diff(x))[0]} {u1:trans[u(x)].diff(x).subs({v1:v(y).diff(y).subs({y:y(x)})})}

eq1 = u(x).diff(x, x) - (exp(u(x)*x)*u(x).diff(x))