mmf.math.integrate¶
| acceleration | This module provides some techniques for sequence acceleration. |
| integrate_1d | |
| multidimen | Multi-dimensional integration. |
| odepack | |
| IntegrationError([mesg, res, err]) | Error during integration. |
| IntParam([c]) | These parameters control the integration. |
| quad(f, a, b[, epsabs, epsrel, limit, points]) | An improved version of integrate.quad that does some argument checking and deals with points properly. |
| mquad(f, a, b[, abs_tol, verbosity, fa, fb, ...]) | Return (res, err) where res is the numerically evaluated |
| spherical_int(f[, points, param]) | This function computes the spherical integral of the function |
| spherical_int_no_r(f[, points, param]) | This function computes the spherical integral of the function |
| spherical_int2(f[, specialR, specialX, param]) | This function computes the spherical integral of the function |
| spherical_int2_no_r(f[, specialR, specialX, ...]) | This function computes the spherical integral of the function |
| angular_average(f[, r, theta, phi, param]) | Compute the integral of f(r, cos(theta), phi) in spherical coordinates. |
| angular_average_no_r(f[, r, theta, phi, param]) | Compute the integral of f(r, cos(theta), phi)/r^2 in spherical coordinates. |
| adaptive_angular_average(f, r[, theta, phi, ...]) | Compute the integral of f(r, cos(theta), phi) in spherical coordinates using multi-dimensional adaptive methods. |
| adaptive_angular_average_no_r(f, r[, theta, ...]) | Compute the integral of f(r, cos(theta), phi)/r^2 in spherical coordinates. |
| ssum(xs) | Return (sum(xs), err) computed stably using Kahan’s summation |
| ksum(a, b[, c]) | Return (a+b, c) computed stably using Kahan’s summation |
| exact_add(a, b) | Exact addition. |
| exact_sum(xs) | Compute the sum of all values in xs exactly. |
| Richardson(f[, ps, l, n0]) | Compute the Richardson extrapolation of 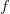 given the function given the function |
| rsum(f[, N0, ps, l, abs_tol, rel_tol]) | Sum f using Richardson extrapolation. |
| levin_sum(f_term[, N0, offset, Nmin, Nmax, ...]) | Sums the terms f_term(N) using the Levin u-transformation. |
| mc_angular_average(f[, r, theta, phi, param]) | Compute the integral of f(r, cos(theta), phi) in spherical coordinates using monte-carlo. |
| mc_integrate(f, a, b[, abs_tol, rel_tol, w]) | Performs a Monte-Carlo integration of f(x) over the |
Inheritance diagram for mmf.math.integrate:
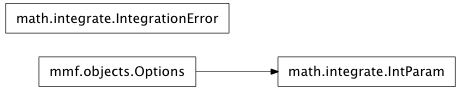
Integration Utilities.
- class mmf.math.integrate.IntegrationError(mesg=None, res=None, err=None)¶
Bases: exceptions.Exception
Error during integration.
- __init__(mesg=None, res=None, err=None)¶
- class mmf.math.integrate.IntParam(c=None, **kwargs)¶
Bases: mmf.objects.Options
These parameters control the integration.
- __init__(c=None, **kwargs)¶
- AbsTol = 1e-18¶
- Dimension = 3¶
- Lambda = inf¶
- Nfunc = 100000¶
- RecLimit = 10000¶
- RelTol = 1e-12¶
- Verbose = True¶
- mmf.math.integrate.quad(f, a, b, epsabs=1e-12, epsrel=1e-08, limit=1000, points=None, **kwargs)¶
An improved version of integrate.quad that does some argument checking and deals with points properly.
Return (ans, err).
Examples
>>> def f(x): return 1./x**2 >>> (ans, err) = quad(f, 1, np.inf, points=[]) >>> abs(ans - 1.0) < err True >>> (ans, err) = quad(f, 1, np.inf, points=[3.0, 2.0]) >>> abs(ans - 1.0) < err True
- mmf.math.integrate.mquad(f, a, b, abs_tol=1e-12, verbosity=0, fa=None, fb=None, save_fx=False, res_dict=None, max_fcnt=10000, min_step_size=None, norm=<function <lambda> at 0xb55f3f0>, points=[])¶
Return (res, err) where res is the numerically evaluated integral using adaptive Simpson quadrature.
mquad tries to approximate the integral of function f from a to b to within an error of abs_tol using recursive adaptive Simpson quadrature. mquad allows the function y = f(x) to be array-valued. In the matrix valued case, the infinity norm of the matrix is used as it’s “absolute value”.
Parameters : f : function
Possibly array valued function to integrate. If this emits a NaN, then an AssertionError is raised to allow the user to optimize this check away (as it exists in the core of the loops)
a, b : float
Integration range (a, b)
fa, fb : float
f(a) and f(b) respectively (if already computed)
abs_tol : float
Approximate absolute tolerance on integral
verbosity : int
Display info if greater than zero. Shows the values of [fcnt a b-a Q] during the iteration.
save_fx : bool
If True, then save the abscissa and function values in res_dict.
res_dict : dict
Details are stored here. Pass a dictionary to access these. The dictionary will be modified.
fcnt : Number of function evaluations. xy : List of pairs (x, f(x)) if save_fx is defined.
max_fcnt : int
Maximum number of function evaluations.
min_step_size : float
Minimum step size to limit recursion.
norm : function
Norm to use to determine convergence. The absolute error is determined as norm(f(x) - F).
points : [float]
List of special points to be included in abscissa.
Notes
Based on “adaptsim” by Walter Gander. Ref: W. Gander and W. Gautschi, “Adaptive Quadrature Revisited”, 1998. http://www.inf.ethz.ch/personal/gander
Examples
Orthogonality of planewaves on [0, 2pi]
>>> def f(x): ... v = np.exp(1j*np.array([[1.0, 2.0, 3.0]])*x) ... return v.T.conj()*v/2.0/np.pi >>> ans = mquad(f, 0, 2*np.pi) >>> abs(ans - np.eye(ans.shape[0])).max() < _abs_tol True
>>> res_dict = {} >>> def f(x): return x**2 >>> ans = mquad(f, -2, 1, res_dict=res_dict, save_fx=True) >>> abs(ans - 3.0) < _abs_tol True >>> x = np.array([xy[0] for xy in res_dict['xy']]) >>> y = np.array([xy[1] for xy in res_dict['xy']]) >>> abs(y - f(x)).max() 0.0
>>> def f(x): return 1.0/np.sqrt(x) + 1.0/np.sqrt(1.0-x) >>> abs(mquad(f, 0, 1, abs_tol=1e-8) - 4.0) < 2e-7 True
>>> def f(x): ... if x < 0: ... return 0.0 ... else: ... return 1.0 >>> abs(mquad(f, -2.0, 1.0) - 1.0) < 1e-10 True
>>> def f(x): return 1./x >>> mquad(f, 1, np.inf) Traceback (most recent call last): ... ValueError: Infinite endpoints not supported.
- mmf.math.integrate.spherical_int(f, points=None, param=IntParam({'RelTol': 1e-12, 'AbsTol': 1e-18, 'Verbose': True, 'RecLimit': 10000, 'Nfunc': 100000, 'Dimension': 3, 'Lambda': inf}))¶
This function computes the spherical integral of the function ‘f(r)’ in d=param.Dimension dimensions.
‘points’ should be a list of radii where the function may be discontinuous.
The integrals are controlled by the parameters: param.Dimension: Dimension. param.Lambda: Radial cutoff. param.AbsTol/Omega_d: Absolute tolerance. param.RelTol: Relative tolerance. param.RecLimit: Recursion Limit. param.Verbose: Verbosity.
The tolerances work as follows: if the answer is large then the relative tolerance is less than RelTol (though the absolute tolerance may be larger). If the answer is small, the absolute tolerance is less than AbsTol (though the relative tolerance may be larger).
- mmf.math.integrate.spherical_int_no_r(f, points=None, param=IntParam({'RelTol': 1e-12, 'AbsTol': 1e-18, 'Verbose': True, 'RecLimit': 10000, 'Nfunc': 100000, 'Dimension': 3, 'Lambda': inf}))¶
This function computes the spherical integral of the function ‘f(r)’ in d=param.Dimension dimensions. It does not include the factor of r^(d-1) which must be included in ‘f’: i.e. this function computes the spherical integral of ‘f(r)/r^(d-1)’ but does include the spherical measure factor Omega_d = param._spherical_measure().
‘points’ should be a list of radii where the function may be discontinuous.
The integrals are controlled by the parameters: param.Dimension: Dimension. param.Lambda: Radial cutoff. param.AbsTol/Omega_d: Absolute tolerance. param.RelTol: Relative tolerance. param.RecLimit: Recursion Limit. param.Verbose: Verbosity.
The tolerances work as follows: if the answer is large then the relative tolerance is less than RelTol (though the absolute tolerance may be larger). If the answer is small, the absolute tolerance is less than AbsTol (though the relative tolerance may be larger).
- mmf.math.integrate.spherical_int2(f, specialR=None, specialX=None, param=IntParam({'RelTol': 1e-12, 'AbsTol': 1e-18, 'Verbose': True, 'RecLimit': 10000, 'Nfunc': 100000, 'Dimension': 3, 'Lambda': inf}))¶
This function computes the spherical integral of the function ‘f(r, costheta)’ in d=param.Dimension dimensions. Thus, this computes the spherical integral of ‘f(r, <r, q>/r/q)’ where <r, q> = r*q*cos(theta).
The functions ‘specialR(x)’ and ‘specialX(p)’, if not ‘None’ should compute possible discontinuities in the integrand. If exactly one of these is defined, then that variable is computed as in the inner integral.
The integrals are controlled by the parameters: param.Dimension: Dimension. param.Lambda: Radial cutoff. param.AbsTol/Omega_d: Absolute tolerance. param.RelTol: Relative tolerance. param.RecLimit: Recursion Limit. param.Verbose: Verbosity.
The tolerances work as follows: if the answer is large then the relative tolerance is less than RelTol (though the absolute tolerance may be larger). If the answer is small, the absolute tolerance is less than AbsTol (though the relative tolerance may be larger).
- mmf.math.integrate.spherical_int2_no_r(f, specialR=None, specialX=None, param=IntParam({'RelTol': 1e-12, 'AbsTol': 1e-18, 'Verbose': True, 'RecLimit': 10000, 'Nfunc': 100000, 'Dimension': 3, 'Lambda': inf}))¶
This function computes the spherical integral of the function ‘f(r, costheta)’ in d=param.Dimension dimensions. It does not include the factor of r^(d-1) which must be included in ‘f’, but does include the spherical measure factor Omega_d = param._spherical_measure(). Thus, this computes the spherical integral of ‘f(r, <r, q>/r/q)/r^(d-1)’ where <r, q> = r*q*cos(theta).
The functions ‘specialR(x)’ and ‘specialX(p)’, if not ‘None’ should compute possible discontinuities in the integrand. If exactly one of these is defined, then that variable is computed as in the inner integral.
The integrals are controlled by the parameters: param.Dimension: Dimension. param.Lambda: Radial cutoff. param.AbsTol/Omega_d: Absolute tolerance. param.RelTol: Relative tolerance. param.RecLimit: Recursion Limit. param.Verbose: Verbosity.
The tolerances work as follows: if the answer is large then the relative tolerance is less than RelTol (though the absolute tolerance may be larger). If the answer is small, the absolute tolerance is less than AbsTol (though the relative tolerance may be larger).
- mmf.math.integrate.angular_average(f, r=inf, theta=3.141592653589793, phi=6.283185307179586, param=IntParam({'RelTol': 1e-12, 'AbsTol': 1e-18, 'Verbose': True, 'RecLimit': 10000, 'Nfunc': 100000, 'Dimension': 3, 'Lambda': inf}))¶
Compute the integral of f(r, cos(theta), phi) in spherical coordinates.
If the input parameters are numbers, the integration ranges are taken from 0 to these numbers. Otherwise, they must specify ranges. This is useful for computing the angular average of a function along the z-axis (such as a line-of-sight integral with a fixed angular field of view).
The integrals are controlled by the parameters: param.AbsTol: Absolute tolerance. param.RelTol: Relative tolerance. param.RecLimit: Recursion Limit. param.Verbose: Verbosity.
- mmf.math.integrate.angular_average_no_r(f, r=inf, theta=3.141592653589793, phi=6.283185307179586, param=IntParam({'RelTol': 1e-12, 'AbsTol': 1e-18, 'Verbose': True, 'RecLimit': 10000, 'Nfunc': 100000, 'Dimension': 3, 'Lambda': inf}))¶
Compute the integral of f(r, cos(theta), phi)/r^2 in spherical coordinates. (In other words, no factor of r^2 is added: f must compute this volume factor.)
If the input parameters are numbers, the integration ranges are taken from 0 to these numbers. Otherwise, they must specify ranges. This is useful for computing the angular average of a function along the z-axis (such as a line-of-sight integral with a fixed angular field of view).
The integrals are controlled by the parameters: param.AbsTol: Absolute tolerance. param.RelTol: Relative tolerance. param.RecLimit: Recursion Limit. param.Verbose: Verbosity.
- mmf.math.integrate.adaptive_angular_average(f, r, theta=3.141592653589793, phi=6.283185307179586, specialR=None, param=IntParam({'RelTol': 1e-12, 'AbsTol': 1e-18, 'Verbose': True, 'RecLimit': 10000, 'Nfunc': 100000, 'Dimension': 3, 'Lambda': inf}), _f=None)¶
Compute the integral of f(r, cos(theta), phi) in spherical coordinates using multi-dimensional adaptive methods.
If the input parameters are numbers, the integration ranges are taken from 0 to these numbers. Otherwise, they must specify ranges. This is useful for computing the angular average of a function along the z-axis (such as a line-of-sight integral with a fixed angular field of view).
specialR can be used to specify point at which to force evaluation. This can be used to ensure that features are not missed.
The integrals are controlled by the parameters: param.AbsTol: Absolute tolerance. param.RelTol: Relative tolerance. param.Nfunc: Maximum number of function evals. param.Verbose: Verbosity.
- mmf.math.integrate.adaptive_angular_average_no_r(f, r, theta=3.141592653589793, phi=6.283185307179586, specialR=None, param=IntParam({'RelTol': 1e-12, 'AbsTol': 1e-18, 'Verbose': True, 'RecLimit': 10000, 'Nfunc': 100000, 'Dimension': 3, 'Lambda': inf}))¶
Compute the integral of f(r, cos(theta), phi)/r^2 in spherical coordinates. (In other words, no factor of r^2 is added: f must compute this volume factor.)
If the input parameters are numbers, the integration ranges are taken from 0 to these numbers. Otherwise, they must specify ranges. This is useful for computing the angular average of a function along the z-axis (such as a line-of-sight integral with a fixed angular field of view).
The integrals are controlled by the parameters: param.AbsTol: Absolute tolerance. param.RelTol: Relative tolerance. param.Nfunc: Maximum number of function evals. param.Verbose: Verbosity.
- mmf.math.integrate.ssum(xs)¶
Return (sum(xs), err) computed stably using Kahan’s summation method for floating point numbers. (C++ version using weave).
>>> N = 10000 >>> l = [(10.0*n)**3.0 for n in reversed(xrange(N+1))] >>> ans = 250.0*((N + 1.0)*N)**2 >>> (ssum(l)[0] - ans, sum(l) - ans) (0.0, -5632.0)
Here is an example of the Harmonic series. Series such as these should be summed in reverse, but ssum should do it well. >>> sn = 1./np.arange(1, 10**4) >>> Hn, Hn_err = exact_sum(sn) >>> ans, err = ssum(sn) >>> abs(ans - Hn) < err True >>> abs(sum(sn) - Hn) < err # Normal sum not good! False >>> abs(sum(list(reversed(sn))) - Hn) < err # Unless elements sorted True
Here is an example where the truncation errors are tested. >>> N = 10000 >>> np.random.seed(3) >>> r = np.random.randint(-2**30, 2**30, 4*N) >>> A = np.array([long(a)*2**90 + long(b)*2**60 + long(c)*2**30 + long(d) ... for (a, b, c, d) in zip(r[:N], r[N:2*N], r[2*N:3*N], r[3*N:4*N])]) >>> B = A.astype(float)/3987.0 # Introduce truncation errors >>> exact_ans = A.sum() >>> ans, err = ssum(B) >>> ans *= 3987.0 >>> err *= 3987.0 >>> exact_err = abs(float(long(ans) - exact_ans)) >>> exact_err < err True >>> exact_err < err/1000.0 False
ssum runs less than 8 times slower than a regular sum. >>> import time >>> n = 1./np.arange(1, 2**10) >>> t = time.time();tmp = n.sum();t0 = time.time() - t; >>> t = time.time();tmp = ssum(n);t1 = time.time() - t; >>> t1 < 8.0*t0 True
- mmf.math.integrate.ksum(a, b, c=0.0)¶
Return (a+b, c) computed stably using Kahan’s summation method for floating point numbers where c is the carry.
>>> (x, c) = ksum(2e100, 2e51) >>> x 2e+100 >>> c 2e+51
- mmf.math.integrate.exact_add(a, b)¶
Exact addition. Return (x, err) so that using exact addition x + err == a + b but using floating point x + err == x
This is based on the fact that, with IEEE floating point if abs(b) <= abs(a):
x = a + b # Floating point sum err = (a - x) + b # Exact error>>> exact_add(1e18, 1) (1e+18, 1.0)
- mmf.math.integrate.exact_sum(xs)¶
Compute the sum of all values in xs exactly.
Return (ans, err) where err is an array whose sum is the exact err, and ans is the sum.
>>> (x, err) = exact_sum([2e100, 2e51, 2, 2e-50, -2]) >>> x 2e+100 >>> err [2e+51, 2e-50]
- mmf.math.integrate.Richardson(f, ps=None, l=2, n0=1)¶
Compute the Richardson extrapolation of
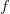 given the function
given the function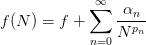
The extrapolants are stored in the array S`[n, s] where `S[n, 0] = f(n0*l**n) and S[n, s] is the s’th extrapolant.
Note
It is crucial for performance that the powers
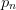 be properly
characterized. If you do not know the form of the errors, then consider
using a non-linear acceleration technique such as levin_sum().
be properly
characterized. If you do not know the form of the errors, then consider
using a non-linear acceleration technique such as levin_sum().Parameters : ps : iterable
Iterable returning the powers
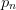 . To generate the sequence :math:`p_0 + m
. To generate the sequence :math:`p_0 + md_p` for example, use itertools.count``(p0, dp)().
Examples
Here we consider
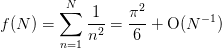
>>> def f(N): return sum(np.arange(1, N+1, dtype=float)**(-2)) >>> r = Richardson(f, l=3, n0=2) >>> for n in xrange(9): ... x = r.next() >>> err = abs(x - pi**2/6.0) >>> assert err < 1e-14, `err`
Now some other examples with different p values:
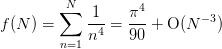
>>> def f(N): return sum(arange(1, N+1, dtype=float)**(-4)) >>> r = Richardson(f, ps=itertools.count(3,1)) >>> for n in xrange(8): ... x = r.next() >>> err = abs(x - pi**4/90.0) >>> assert err < 1e-14, `err`
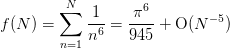
>>> def f(N): return sum(arange(1, N+1, dtype=float)**(-6)) >>> r = Richardson(f, ps=itertools.count(5)) >>> for n in xrange(7): ... x = r.next() >>> err = abs(x - pi**6/945.0) >>> assert err < 1e-14, `err`
Richardson works with array valued functions:
>>> def f(N): return array([sum(arange(1, N+1, dtype=float)**(-2)), ... sum(arange(1, N+1, dtype=float)**(-4))]) >>> r = Richardson(f, l=3, n0=2) >>> for n in xrange(7): ... x = r.next() >>> err = abs(x - array([pi**2/6.0, pi**4/90.0])).max() >>> assert err < 1e-13, `err`
It also worksworks for complex valued functions:
>>> def f(N): return (sum(arange(1, N+1, dtype=float)**(-2)) + ... 1j*sum(arange(1, N+1, dtype=float)**(-4))) >>> r = Richardson(f, l=3, n0=2) >>> for n in xrange(7): ... x = r.next() >>> err = abs(x - (pi**2/6.0+1j*pi**4/90.0)) >>> assert err < 1e-13, `err`
- mmf.math.integrate.rsum(f, N0=0, ps=None, l=2, abs_tol=1e-12, rel_tol=1e-08)¶
Sum f using Richardson extrapolation.
- mmf.math.integrate.levin_sum(f_term, N0=0, offset=0.0, Nmin=5, Nmax=None, abs_tol=1e-12, rel_tol=1e-08)¶
Sums the terms f_term(N) using the Levin u-transformation.
Returns (ans, err)
The answer is sum_{n=N0}^{inf}(f_term(n))+offset.
Parameters : f_term : function
offset : float
The offset is used to help estimate the relative error properly.
Nmin : int
Minimum number of terms to give to the levin_sum procedure.
Nmax : int
Maximum number of terms.
abs_tol : float
Desired absolute tolerance (this may not be achieved but will help the routine bail out.)
rel_tol : float
Desired absolute tolerance (this may not be achieved but will help the routine bail out.)
Examples
>>> def f(n): ... return 1./n/n >>> (ans, err) = levin_sum(f, N0=1, abs_tol=1e-10, rel_tol=0) >>> abs(ans - np.pi**2/6) < err True >>> err < 1e-10 True
>>> def f(n, p=2): ... "Terms for Riemann Zeta function" ... return 1./n**p >>> (ans, err) = levin_sum(f, N0=1, abs_tol=1e-10, rel_tol=0) >>> abs(ans - np.pi**2/6) < err True >>> err < 1e-10 True
>>> def f(n, x=-15.0): ... return x**n/sp.misc.factorial(n) >>> (ans, err) = levin_sum(f, N0=0, abs_tol=1e-10, rel_tol=0) >>> abs(ans - np.exp(-15.0)) < err True >>> err < 5e-10 True
- mmf.math.integrate.mc_angular_average(f, r=inf, theta=3.141592653589793, phi=6.283185307179586, param=IntParam({'RelTol': 1e-12, 'AbsTol': 1e-18, 'Verbose': True, 'RecLimit': 10000, 'Nfunc': 100000, 'Dimension': 3, 'Lambda': inf}))¶
Compute the integral of f(r, cos(theta), phi) in spherical coordinates using monte-carlo.
If the input parameters are numbers, the integration ranges are taken from 0 to these numbers. Otherwise, they must specify ranges. This is useful for computing the angular average of a function along the z-axis (such as a line-of-sight integral with a fixed angular field of view).
The integrals are controlled by the parameters: param.AbsTol: Absolute tolerance. param.RelTol: Relative tolerance. param.RecLimit: Recursion Limit. param.Verbose: Verbosity.
- mmf.math.integrate.mc_integrate(f, a, b, abs_tol=0.01, rel_tol=0.01, w=None)¶
Performs a Monte-Carlo integration of f(x) over the N-dimensional rectangular region a[n] < x[n] < b[n] where N is the length of a and b. If f_accept is defined, then points will be weighted by w(x). Note that w(x) can be used to define more complicated boundaries.
>> f = lambda x:x[0]**2+x[1]**2+x[2]**2 >> a = [0., 0., 0.] >> b = [2., 2., 2.] >> mc_integrate(f, a, b)