Version 1.0 - Draft, 4/10/97
Copyright ©: 1995, 1996, 1997 George E. Mobus. All rights reserved.
Adaptrode Learning and Autonomous Agents
George E. Mobus
Previous Affiliation: Western Washington University
Current Affiliation: University of Washington Tacoma, Institute of Technology
Abstract
The adaptrode model is viewed from the perspective of autonomous, artificial agent technology. Real autonomy, it is argued, comes from an agent's capacity to adapt to a nonstationary, real-world environment. This requires knowledge acquisition through real-time, on-line and life-time learning. This page provides an overview of the use of adaptrode-based machine learning in agents to achieve this end. It includes a summary of the adaptrode mechanism and its correspondence to biological systems.
Introduction
An adaptrode is a unique linear, multi-staged adaptive filter which models the memory trace encoding mechanism of the synaptic junction of living neurons. It produces a response to the current primary input which is proportional not only to that input, but also to both the history of the input and, optionally, the history of secondary correlated inputs. This device is the basis of a new machine learning approach that addresses a critical problem in the construction of autonomous (so-called intelligent) agents. That problem is the ability to carry on lifelong learning in an open world environment. Open worlds are those for which no fixed boundary conditions can be guaranteed. They are characterized by chaotic dynamics and nonstationary processes leading to significant difficulties in precise mathematical formulations which could be used to design strictly rational agents. The states of such worlds are difficult, if not impossible to predict, especially for longer time scales. This is the nature of the "real world" in which animals must compete for critical resources to survive and reproduce. That animals have succeeded in doing so atests to the efficacy of adaptation and learning.The Need for Learning in Autonomous Agents
Further progress in autonomous agent technology depends on the development of suitable machine learning algorithms that will provide agents with on-going adaptive capabilities. Autonomy depends on the ability of an agent to acquire new knowledge in the course of its experiences. Machine learning is now one of the most active research areas in artificial intelligence. Much of this work has centered around pattern recognition and categorization in fixed worlds. The adaptrode is a unique multi-time scale, linear filter that records memory traces of suitably encoded real world signals. Embedded in a neural architecture it provides a means for continuous adaptation to changing conditions in an open, evolving world.Real World Considerations
The real world into which agents are expected to go is not just dynamic it is also nonstationary, constantly changing. This means that patterns of association change over time in indeterminate ways. Typical machine learning systems have been monotonic with respect to the gain in knowledge treating the world as a closed system. So long as the agent is exposed to environments that are indeed closed, even if highly stochastic, such a scheme can work reasonably well.Natural environments are not closed worlds. The immediate (read accessible) environment of the agent is itself embedded in, and interacts with, a larger environment. And, in turn that environment is embedded in a still larger one. While this regress is not necessarily infinite in any absolute sense (i.e., the Universe may be closed), so far as the agent is concerned it is effectively so due to the limits of accessibility in time. Environmental interactions that took place in a prior time period on the periphery of the agent's immediate environment can alter relationships that the agent has already learned. The agent's knowledge is thus rendered less useful and certainly suboptimal.
Adding to the complexity of real worlds, the time scales of these indeterminate changes are themselves intedeterminate. Anything from catastrophe to subtle, long-term changes can ensue depending on the dynamics of the interaction and the spatial scale involved. An earthquake. resulting from eons of pressure buildup in the tectonic plates, can alter the landscape in an instant. Changes in solar radiation due to sun spot activity will cause colder or warmer seasons over many years. Animals, our best examples of autonomous agents in real world environments, need to adapt to a wide range of changing conditions to survive in the real world.
As pointed out, traditionally machine learning has been pursued under the closed world assumption. In large part this pursuit was motivated by a simple expediency. Closed worlds are subject to tractable mathematical analysis. One can offer proofs that a given algorithm produces a claimed result. The systems are aimed at stationary targets. The problem has been that when these same systems are aimed at different targets from the real world they fail to produce the promised results.
Lifelong Learning
Autonomy means being able to make independent decisions while the agent is deployed on a mission. We can envision some missions extending over significant periods of time during which there would be no opportunity for re-training the agent. Under such circumstances the agent must be capable of learning continuously as the environment changes. Such a capability has been called "lifelong learning".One problem that faces many researchers who have attempted to address this issue is the destructive interference of new information with respect to old knowledge. In effect, continuous learning causes a "washing out" of old knowledge. For example suppose a relationship between A and B has been learned such that the occurrence of A generates a response to B. If at some later time should this relationship be altered in the extant world, the learner would have to acquire whatever new relationship might have developed, say between C and B. In order to do so, many learning systems, particularly symbolic-based representation systems, either need to forget the older association or archive the prior association indexed by some time stamp. In the former case, the new knowledge requires the obliteration of the old. In the latter case, the system may be quickly overwhelmed by the increase in size of the knowledge base. Additionally, recall, say for reasoning purposes, is burdened by extra processing overhead associated with temporal indexing.
The adaptrode overcomes these problems by incorporating a multi-stage, differential memory trace mechanism that allows the simultaneous encoding of associations that separate in time scale. It records not only short-term memory traces but intermediate and long-term traces as well. These traces are cascaded and precedence ordered, from short-term to long-term. Coupled with the adaptrode's normal decay method, this means that traces that are not reinforced over time will fade, rapidly in the short-term trace, more slowly in intermediate traces and very slowly in long-term traces. Thus, the adaptrode can maintain a very long memory trace of an association that once was the rule but has not been sustained. This trace is a faint shadow compared to other short-term traces that might compete for processing resources. From the standpoint of lifelong learning, this makes it possible for the adaptrodes in a network to retain old knowledge without interfering with new knowledge.
This capacity is extremely important. It is not infrequent that associations which have been true for a long time, and then due to short-term changes in the environment, are no longer true over the duration of the short-term changes. Subsequently, the longer-term rule will once again become true. That is, the environment may undergo short-term or transitory changes that are not, technically speaking, noise. Such changes create a need to learn new associations in order to survive. On the other hand, the factors which wrought such a change could eventually revert to the prior condition. The older relationships would again become the norm and the older association knowledge would become operative again. For systems that suffer from destructive interference, the learner would have to start learning anew each time these sorts of transitory changes occurred.
Multiple Time Scale Learning
As pointed out, changes that take place in the open world do so over varying temporal scales. An agent can remain autonomous over the course of very long mission times if it is capable of adapting in multiple time scales. The adaptrode provides a cascade of memory trace mechanisms that operate over lengthening time domains. A short-term trace records recent events and fades (forgets) in a short time as well. An intermediate-time trace mechanism is activated by the short-term trace and records a discounted average level of the short-term trace. Similarly, a long-term trace mechanism, activated by the intermediate-term trace, records a discounted average level of the intermediate-term trace. In theory, any number of intermediate-term levels could be defined such that very long time scales could be accommodated or intermediate temporal resolution increased.Semantic-driven Associative Learning
All learning systems attempt to encode associative links between suitable representations of external objects (patterns). For most machine learning systems this is a syntactically-driven process. For example supervised learning mechanisms such as the error backpropogation method used in multi-layer feedforward neural networks operate irrespective of the "meaning" of the patterns being associated. Input patterns are mapped to desired output patterns. The network itself, aside from capacity considerations, could be applied to any similar set of mappings without regard to the "natural" relationships being associated. This is perfectly legitimate for the employment of neural nets to capture some difficult to specify, but predetermined function.A brain is not a tabula rasa. Though malleable, it is not to be molded in any old shape. It is organized, genetically, to be sensitive to specific kinds of patterns at specific times during the development of the juvenile. Learning in animals, and, according to the latest findings of neuroscience, for humans as well, is guided largely by the meaning of the patterns encountered. Such meaning is rooted (or grounded) in physiological needs, the homeostatic milieu of the body. It is fixed by evolution and underlies a surprising amount of rational thinking [see "Descartes' Error" by Antonio Damasio]. Thus not just anything is learned. What is learned is linked, through numerous levels of association to be sure, to what is important to the biology of the learner. This is called semantic-driven learning. Evolutionarilly-speaking it has been a blindingly obvious success. It would be a worthy model for autonomous agent learning.
A network of adaptrode-based neuron-like processing elements can be constructed which learn associations based on semantics. That is, the network can extract meaningful associations from the seeming chaos of patterns impinging on the learning agent. This is accomplished by gating the influence of the short-term memory trace on the intermediate-term trace with a correlation term, derived from a second signal source. The correlation is not simple however. The second signal must arrive after some small time lapse since the onset of the primary signal. If the second signal arrives before the primary or even simultaneously, no intermediate-term encoding ensues. The secondary signal comes from a special input to the neuron-like processing element. This signal conveys meaning to the learner. It signals some factor in the environment which is deemed, a priori, requisite of a response. In animals such a signal constitutes a stimulus-response circuit, a hard-wired, genetically-determined condition-action pair. The adaptrode's primary signal, however, comes from what might be called "free sense" transducers. Signals from such transducers (note that this could be another neuron) do not convey any necessary meaning. They simply inform the neuron about states of the relevant environment at any given instant.
The adaptrode provides what Damasio calls a convergence point for these signals. One, an arbitrary world-state variable, another a world-state variable with direct consequences for the agent. The one arriving early, the other lagging slightly. The result of this temporal offset, if it happens reliably over longer time scales, is that the primary signal takes on the same significance as the secondary. In other words, the primary, "free sense" signal comes to represent the onset of the secondary meaningful one. It effectively becomes a predictor of the meaningful signal. An important survival advantage can easily be seen in this scheme. Prediction of an impending consequential event gives the learner a jump start to respond. The learner becomes proactive with respect to the consequence. Early action can tend to reduce costs of merely reacting to stimuli.
Adding Adaptive Memory to Persistent Objects
A simple example of an autonomous adaptive agent is a persistent object manager. Consider bookmarked URLs. Many users typically use bookmarks to preserve the location of web pages that they wish to revisit. The number of bookmarks can grow prodigiously. These are simply line items in a growing database. But as is the case with monotonic growing entities a time comes when the list is out of control. The reality is that most people keep things for fear that they may need them later. So the bookmarks pile up while old ones never get revisited. And in truth, in the dynamic (some would say chaotic) environment of the web many old bookmarks end up pointing nowhere.In other words bookmark objects age. How can these objects be managed in such a way that old, unused or unimportant items can be readily identified and made candidates for disposal? One simple approach is to attach an adaptrode to each URL. Each time the page is viewed, it results in an excitation of the primary input to the adaptrode. Frequent viewing would result in non-zero short-term trace values. Periodic surveys of these traces on all adaptrodes would quickly reveal zero valued traces. But the adaptrode goes beyond this simplistic scheme. Suppose that the viewing of the page results in a click-through to another page or resource (e.g., ftp's file). This would be a clear indication that the page was meaningful in some sense. Thus a secondary signal to the adaptrode would gate short-term memory into an intermediate-term trace. The adaptrode would remember the bookmarked page as a predictor that something useful might be obtained by the user.
A survey of non-zero valued intermediate-term traces would provide a list of candidate pages for a further stage of memory encoding. A user could periodically be asked to explicitly rate the page bookmarked for its value. The rating would be the basis for a final gating of the intermediate-term trace into long-term memory. Effectively, an adaptrode in which the long-term trace is non-zero is effectively permanent by virtue of frequency of use, resulting in the magnitudes of short-term and intermediate-term traces being high, and the long decay time for long-term traces.
Memory traces do fade however. Over time, even the long-term trace will decay toward zero. Unless a page is frequented over the time scale into which it is encoded, its adaptrode will eventually have a zero valued short-term trace. It will become a candidate for removal from the list. The user could, of course, be given the option to save the page URL anyway, or archive it perhaps. But the manager agent will have done its duty in keeping track of what the user actually does with the resources she has squirreled away.
And that is the key to agent usefulness. Embodied in the memory traces of the adaptrodes attached to those many bookmarked URLs is the pattern of actual user habit/thinking. The agent has learned a great deal about the user's needs by observing the user's behavior. It can make informed suggestions to the user that would be actually useful rather than intrusive.
Bookmarks are just one example of persistent objects that will depend on user's needs. There are obviously many more examples of such objects that do now, or will soon populate cyberspace. Adaptrodes and agents based on this learning mechanism represent a way to add true intelligence - that is semantically based reasoning - to the management of such objects.
How the Adaptrode Works
Extending Memory Traces
The adaptrode mechanism is based strongly on adaptive response in biological systems, of which the modification of synaptic efficacy is one example. Synaptic efficacy - the effectiveness with which a synapse passes on the incomming signal - is thought to be the basis of all forms of learning.There is a long tradition in animal learning theory of modelling the memory trace of a stimulus using the exponential weighted moving avearge (EWMA) method. This method produces a close approximation of data obtained from animal experiments (so-called signature data) for short time scales, but fails to model longer-term memory phenomena very well. The adaptrode evolved from attempts to extend the EWMA method to account for these longer-term phenomena.
Mathematically, EWMA can be stated: 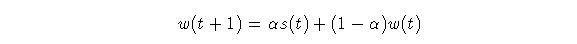 Eq.
1
Eq.
1
Where s(t) is the signal strength at time t; w(t) is the memory trace
variable and alpha is a constant between 0 and 1.
Equation 1 can be rearranged: 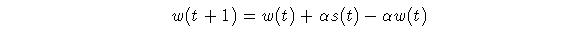 Eq.
2
Eq.
2
The EWMA model of a memory trace suffers from the fact that it falls
off as fast as it rises. It works well to represent the dynamics of a memory
trace over a short span of time, but cannot provide a longer-term trace.
The adaptrode model introduces two "fixes" which improve the retention
of a memory trace while maintaining the leaky integrator characteristics
of the EWMA. The basic adaptrode equation is:  Eq.
3
Eq.
3
The first of two innovations here are the use of a distinct decay factor, differnt from alpha. This factor, delta, is generally much smaller than alpha thus providing for an extended, though still exponential decay of the trace variable. The second inno vation is the use of a shunting factor to bound the growth of w(t). Figure 1 shows a comparison between the adaptrode trace and an EWMA trace. A unit pulse signal is received with each time tick from t = 5 to t = 9. After that the input is held at zero until t = 24. A single pulse is received at that time tick.

Fig. 1. Comparison of Adaptrode and EWMA trace characteristics.
As can be seen in the figure, the Adaptrode trace decays much more slowly than that of the EWMA. Some memory trace remains after the EWMA trace had decayed to (effectively) zero. By selecting appropriate values for alpha and delta, one can obtain sufficiently long, though marginally strong, trace values. In the figure, the adaptrode trace produces a stronger response to the single impulse at t = 24 due to the fact that it started from a higher base.Multiple Time-scale Learning
Taken alone, this would help improve the memory trace performance by extending the trace somewhat, but it cannot provide a sufficiently significant value for later decision discrimination (to be discussed below). As it turns out many real-world signals can be characterized as episodic and sporadic. Episodes are short time scale clusters of excitation. These have indeterminate intensity and duration as well as inter-episodic intervals. In the latter case, it also turns out that many naturally occurring signals are also clustered over longer time scales. Several episodes may follow over a short time, followed by a longer inter-episode interval. Such clusters and inter-cluster periods may have pink-noise or 1/f noise characteristics. For example many inter-episode intervals may be short, some may be intermediate in length while a smaller number will be large. This fractal-like quality may be found at many scales.An example is the impinging signal on a particular hair cell in the ear, tuned to respond to a relatively narrow bandwidth. Owing to the chaotic distribution in space and time of sounds in which this band is a component, the hair cell will be activated in a sporadic and episodic fashion. The hair cell is the source of auditory neural signals that are the basis of sound learning and recognition in the brain. Neurons must be able to encode memory traces of these signals in such a way as to accomodate the episodic/sporadic nature of real-world events.
A third innovation of the adaptrode model, based on the biological properties
of real synapses (see below) is the use of multiple stages to encode traces
over increasingly extended time scales. The basic adaptrode equation is
used recursively but with adjustments to the alpha and delta parameters.
Equation 4 introduces a new index, k, which runs from 0 to some desired
number of time scales or domains less 1 (L). 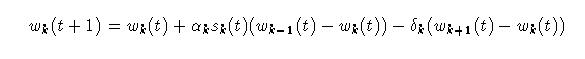 Eq.
4
Eq.
4
Where:
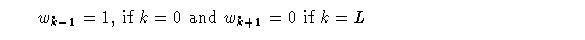
Signals s_k are the secondary inputs to the adaptrode, converging on the primary signal through the cascade of trace variables. This is the correlation factor mentioned above. Its role will be better explained below.
Here I want to focus on the dynamics of the memory traces themselves as the evolve over time with various primary input signals. The secondary signals will be set to 1.0 and fixed. The basic model generated by Equation 4 is shown in Figure 2. Here a three level adaptrode is stimulated over 5 time units starting at time tick 1 (top trace rising for five ticks).
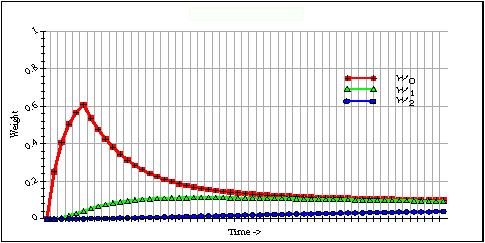
Fig. 2. A three level adaptrode showing the relative values of the three memory trace variables.
As can readily be seen in this figure, the intermediate-term trace, w1, rises slowly, compared with the rise of w0. The latter is stimulated directly by the primary input signal. Similarly, the rise of w2 is much slower than that of w1. This figure is of a non-associative adaptrode, that is, one in which the gating signal of Eq. 4 for k = 1, 2, is clamped at 1.0.To see the relevance of this effect we need to look at how the adaptrode responds to multiple input episodes over time. The actual output of an adaptrode filter, and hence its effect on the system in which it is embedded, is related to the value of w0 in a straightforward way. Let r(t+1) be the response of an adaptrode at time step t. Then:
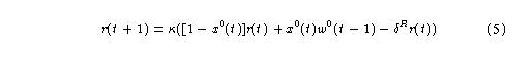 Eq. 5
Eq. 5
The response of an adaptrode is thus either the dominated by the value of w0, if the input is active (in the current examples we are dealing with binary inputs of either one or zero but the arguments here hold for continuous values from one to zero as well), or by an exponentially decaying value of r itself. The trace of r (not shown)_ effectively follows that of w0, but falls off more steepley - it is not bounded from below by w 1.
With the understanding that the response of the adaptrode is dependent on that of w0, we can now look at the effects of multiple input episodes on the dynamics of that response. In Figure 3 is shown the memory traces of a three-level adaptrode similar to that in Figure 2, but with two input episodes separated by some interval of time. The peak response of the adaptrode is approximated by that of w0. As can be seen in the figure, the second response is at a slightly higher value than that of the first episode. It is clear in the figure that this is due to the effects of the longer term memory traces of w1 and w2. It is this dynamic that accounts for the learning taking place in the adaptrode. The unit is learning to respond more strongly as a function of its input history. One can see that not only is the peak higher in the second response, but that the initial response in the second episode is higher than that in the first.
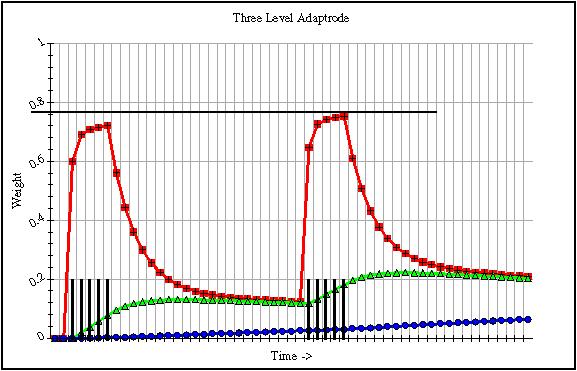
Fig. 3. The dynamics of memory traces, and hence responses, of a three-level adaptrode. Two input episodes are separated by some interval of time, but due to the modulating effects of the longer-term traces, the adaptrode responds marginally more strongly and more quickly to the second event.
Of course, both w1 and w2, themselves decay over time so that if there were no further input events, or sufficiently rare events, these values would tend toward zero and allow w0 to do so also.Most learning situations, to be discussed below, are associative in nature. That is the system encodes a correlation-based association between two or more signals. However, there are important non-associative adaptive responses that play an important role in circuit dynamics. In practice the gating signals, s1, s2, etc. are not clamped at 1.0, but rather are modulated based on prior stage activity. For example, s1 may be switched on (1.0) while the adaptrode response (Eq. 5) is above some threshold value. Similarly, s2 can be switched on while w0 is above w1 by some small epsilon.
Associative Encoding
Single signal response characteristics of the multi-level adaptrode are significant for encoding over multiple time scales. But the larger payoff comes from the fourth innovation in the adaptrode model. The signals, si, for i > 1, can come from sources outside the adaptrode, that is they are secondary signals which, if they arrive in correspondence with the primary signal, gate the increase of the longer-term trace variables according to Equation 4 for levels greater than 0. Essentially this amounts to selective gating of a short-term memory trace into a longer-term trace (or an intermediate-term one) or the encoding of a correlation between the primary and secondary signals. Readout of the encoding comes from the higher and faster response of an adaptrode that codes such a correlation as compared with adaptrodes that do not. Differential, competitive encoding of correlations is the subject of a future page on Basic Associative Networks (BAN) and will be covered in detail there. It is also covered extensively in my paper on causal relation encoding.Briefly, causal relation encoding is the basis for perception of order in the world. It is fundamentally important for agents to be able to predict the occurance of semantically important events based on causal relations (Granger, 1969) with otherwise non-meaningful events as discussed above under the topic of Semantic-driven Associative Learning.
In Correspondence With Biology
In this section I will examine the correspondence between the adaptrode model and what I believe to be the important aspects of the neurophysiology of biological synapses that explain adaptive response.The Biological Basis for an Adaptrode-like Model
As I have shown in my Ph.D. thesis, the adaptrode's dynamics emulate, at least qualitatively, the time-course behavior of the post-synaptic membrane reactivity - the excitatory (inhibitory) post-synaptic potential (E(I)PSP). Daniel Alkon [] has develpoped a model of synaptic efficacy modulation which depends not only on real-time modulation of the post-synaptic membrane patch (specifically the conductance of potassium ion channels), but also on intermediate-term and long-term molecular processes which operate deeper in the post-synaptic compartment cytosol. Changes in portein and mRNA synthesis are implicated and nuclear processes such as DNA activation have been suggested as well.The general model is summarized in Figure 4 and described here.
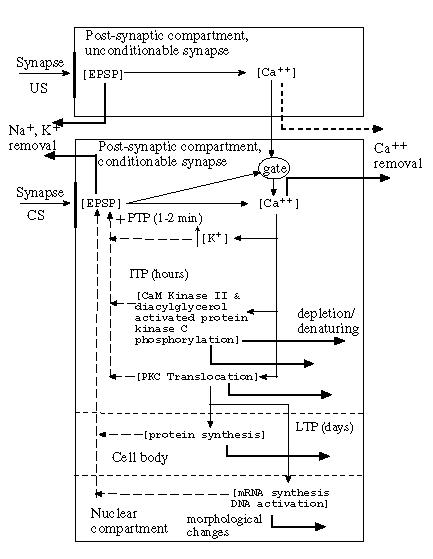
Fig. 4. A summary diagram of the major biophysical processes that transpire in the post-synaptic cytosolic compartment. The diagram elements are explained in the text.
The arrival of an action potential (AP) at a synapse bouton (arrows labelled "Syapse" in the figure) initiates a rapid depolarization of the post-synaptic membrane by triggering the opening of ion channels that allow the influx of Na+, Ca++ and the outflux of K+. The time course nature of a unitary excitatory post-synaptic potential (EPSP) is that it rises sharply with each AP and falls off exponentially fast when the input signal goes to zero. As the EPSP rises rapidly, somewhat slower acting processes, such as the sodium ion pump, work to restore the membrane polarization to its resting potential (actually negative with respect to the outside of the cell).In the figure, variables of interest are contained in square brackets. Thin arrows indicate signals (flows of ions or molecules) which increase a value or slow its decay. Heavy black arrows represent slow decrement processes such as the removal of calcium ions from the cytosol. The dashed arrows represent feedback loops that act principally by down-modulating the slow decrement processes (slow them down even more). Associated with all of the arrows are rate constants (not shown in this figure). Both rate constants of increase (thin arrows) and constants of decay or active removal (heavy arrows) are associated with these processes.
In the following description it is important to recognize that this is my interpretation of the model as expounded by Alkon. I have attempted to extract from his model those factors and their relationships which seem to me to be the important essence of an adaptive process - namely the multiple time scales over which the processes operate and the feedback loops. Any distortion of the biological model as Alkon presents it are entirely due to my interpretation. The intereseted reader is encouraged to take a look at Alkon's work directly for complete clarification.
Following the time-course of events, a series of APs arrive at the synapse labelled "CS" triggering the flux of ions and raising the EPSP. Calcium ions accumulate in the interior of the compartment. At the same time the elevated EPSP opens a "gate" (exact mechanism unknown but it is thought to involve the concentration of calcium prior to the rise in the EPSP) iff there is no previous influx of calcium from another compartment (show above in the figure as the "unconditionable synapse"). Calcium ions from the influx at the conditionable synapse start to accumulate initiating a cascade of biophysical processes which impact the outflux of potassium ions. In the short run, the concentration of calcium ions itself has a down-modulating effect on the potassium outflux. As potassium is retained, this makes the membrane potential more positive with respect to the exterior than it would have been with just the influx of sodium and calcium ions.
Over a somewhat longer time scale, the continued or increased concentration of calcium ions (from the unconditionable synaptic compartment) up-modulates the phosphorylation of potassium ion channel proteins (thus further inhibiting the outflux of potassium) by several processes (e.g., "KaM Kinase II" and others in the diagram). In the event that the second source of calcium is abscent, due either to the gate being closed or the "US" signal not arriving, the compartment concentration of calcium ions is reduced by active and passive removal mechanism so that the longer-term effects on the potassium outflux are minimized. In this case the system returns to a restored state and the memory trace represented by the calcium ion concentration decays to effectively zero.
If, on the other hand, the concentration of calcium ions is longer lived due to the secondary influx, even longer-term processes are set in motion. For example, the mollecule protein kinase C (PKC) moves from the cytosol into the cell membrane where its effectiveness as a phosphoryllator increases. This translocation of a mollecule is presumably a slower processes - slow to build and slow to decay.
All of these events, if they occur, contribute to the continued elevation of the EPSP above its normal resting level. A burst of APs give rise to a transient increase in the EPSP known as post-tetanic potentiation (PSP). If the longer term processes are initiated, the effect is not transitory in the sense that the elevated EPSP may last for several minutes to hours. This is an intermediate-term potentiation (ITP). Finally, if the calcium ion concentration is sustained long enough to effect the translocation of PKC, the elevated EPSP may last for days. This model corresponds with the phenomenon of long-term potentiation (LTP) [c.f. Paul Kelly's Mechanisms Regulating Synaptic Plasticity in Brain].
The model also involves even longer term processes such as the increase in protein synthesis (perhaps ion channel components) that takes place in the cell body (shown as a second compartment under the synaptic compartment and separated by a dashed line). Protein synthesis and transport operates over much longer time scales (as compared with the realtime events associated with the arrival of APs). Additionally, protein denaturing and removal is a relatively slow process so that the accumulation of protein factors that effect the efficacy of the synapse must be long-term.
Finally, Alkon raises the possiblity for really long-term processes which involve the activation of some genes due to second messenger systems activated by the long term location of PKC in the membrane. Such activation involves the integration of presumably different proteins or other structural components which can physically alter the morphology of dendritic compartments. Addmittedly this area is speculative, but some evidence for it has been reported.
Clearly the role of multi-time scale processes in effecting the responsiveness of synapses is an important element in memory traces that extend in time.
Correspondence of the Adaptrode with the Biological Model
The above model describes a cascade of interacting processes the kinetics of which are effected in part by the neighboring processes and in part by rate constants for both the forward and reverse processes or removal processes.The adaptrode is a computational model of principles seen in the biological model. It is not an exact homological mapping from biology to computation. There are several dynamical models of integrate-and-fire neurons involving considerable details of ion channels that are meant to be close representations of real neurons. The adaptrode is not that kind of model. What I have sought to capture was the computational essence of adpativity and apply it to the case of synaptic processing. None the less some homology is in evidence.
For example, the response of the adaptrode (Eq. 5) is roughly equivalent to the EPSP (roughly because it does not itself stay elevated after fall-off in input signal). The concentration of calcium ions is approximated by the level-0 weight, w0. It can also be seen that the other biophysical processes that contribute to extending the reduced outflux of potassium ions are represented in higher level weights. Each weight in the vector of a single adaptrode has both increase (alpha) and decrement (delta) constants corresponding to the kinetic constants associated with the biophysical processes.